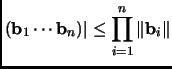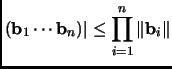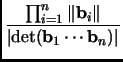Next: Short vectors
Up: Discrete Math, Tenth Problem
Previous: Discrete Math, Tenth Problem
Exercise 1.1 (Hadamard inequality)
Show that if
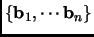
is a basis of
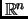
, then
det
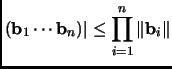
Exercise 1.2
Show that in the previous exercise, there is equality if and only if the basis is orthogonal.
Definition 1.3
The
orthogonality defect of a basis
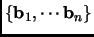
is defined as the quantity:
The following theorem is left as a challenge to the reader.
Theorem 1.4
Every lattice has a basis with orthogonality defect less than
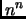
.
Varsha Dani
2003-07-25