Throughout this section,
let
![]() be a vector in
be a vector in
![]() , and let
, and let
![]() be a real number.
We would like to find integers
be a real number.
We would like to find integers
![]() such that
such that
The question is, for what ![]() can we
can we
Recall our second proof of Dirichlet's theorem which used Minkowski's theorem. We examined the matrix:
![\begin{displaymath}
% latex2html id marker 1689\left[
\begin{array}{ccccc}
-1...
...n \\
0 & \ldots & 0 & 0 & \epsilon/Q \\
\end{array}\right]
\end{displaymath}](img59.gif)
We took integer linear combinations of the columns with coefficients
![]() , with
, with
![]() ,
and
,
and
![]() . Setting
. Setting ![]() ,
we get the desired result. The question now is for what value of
,
we get the desired result. The question now is for what value of
![]() can we construct such a vector (not just guarantee its existence).
can we construct such a vector (not just guarantee its existence).
From part (b) of Theorem 2.11, we can find a Lovasz-reduced
basis for the lattice spanned by the columns of this matrix, and
that gives a vector ![]() , such that
, such that
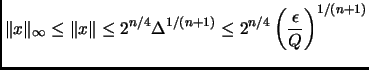 .
.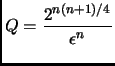 .
.
So for this value of ![]() , Lovasz's Lattice Reduction algorithm
finds a solution in polynomial time.
, Lovasz's Lattice Reduction algorithm
finds a solution in polynomial time.