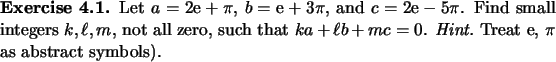
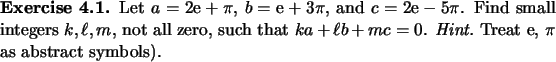
![]()
More generally, given real numbers ![]() , we need integers
, we need integers ![]() , not all zero, such that
, not all zero, such that
![]() . What we would like to know is for what
. What we would like to know is for what ![]() , can we find such integers,
, can we find such integers, ![]() , such that
, such that ![]() ? To this end, we construct the following matrix:
? To this end, we construct the following matrix:
![\begin{displaymath}
% latex2html id marker 1726\left[
\begin{array}{ccccc}
\a...
...\
& \ddots & \\
0 & & \epsilon/Q \\
\end{array}\right]
\end{displaymath}](img73.gif)
(Notice that this is not a square matrix.) Now we would like a vector ![]() , such that
, such that
![]() and
and
![]() . Such a vector with repsect to this matrix would be a solution to our problem. Again applying part b of Theorem 2.11, we know that
. Such a vector with repsect to this matrix would be a solution to our problem. Again applying part b of Theorem 2.11, we know that
![\begin{displaymath}
% latex2html id marker 1751\left[
\begin{array}{ccccc}
\a...
...& 0 \\
& \ddots & \\
0 & & \beta \\
\end{array}\right]
\end{displaymath}](img80.gif)
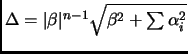 .
.