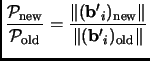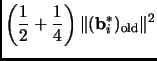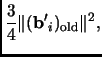Next: Linear programming
Up: Discrete Math, Eleventh Problem
Previous: Discrete Math, Eleventh Problem
Recall that a basis
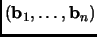 for a lattice is Lovász-reduced if it satisfies the relations:
for a lattice is Lovász-reduced if it satisfies the relations:
-
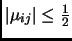 ,
,
-
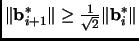 ,
,
where
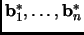 is the Gram-Schmidt orthogonalized sequence
and
is the Gram-Schmidt orthogonalized sequence
and
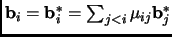 .
In order to prove that Lovász' lattice reduction algorithm
terminates, we introduce the potential function
.
In order to prove that Lovász' lattice reduction algorithm
terminates, we introduce the potential function
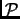 of a basis defined as:
of a basis defined as:
We would like to show that the Lovász algorithm terminates
by observing that in each round, the potential function decreases
by a factor bounded above by some constant 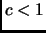 .
Because of this, and the fact that
.
Because of this, and the fact that
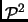 is a positive integer,
we know that the algorithm must terminate in a number of rounds
logarithmic in the initial potential.
is a positive integer,
we know that the algorithm must terminate in a number of rounds
logarithmic in the initial potential.
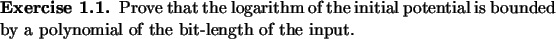
Recall that the ``coefficient reduction'' process
reduces each 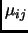 to
to
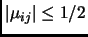 without affecting the orthogonalized sequence and therefore
without affecting the potential function. Once ``coefficient
reduction'' has been performed,
we check the second property. If there is some
without affecting the orthogonalized sequence and therefore
without affecting the potential function. Once ``coefficient
reduction'' has been performed,
we check the second property. If there is some 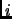 with
with
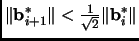 ,
we simply swap these two elements.
This will change the orthogonalized vectors
,
we simply swap these two elements.
This will change the orthogonalized vectors
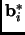 and
and
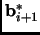 , but the potential is only affected by:
, but the potential is only affected by:
Next we project along the direction of
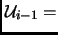 Span
Span .
After this projection, the vectors
.
After this projection, the vectors
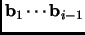 are taken to the zero vector. Denote the projection by
are taken to the zero vector. Denote the projection by
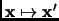 . Now examining
. Now examining
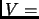 Span
Span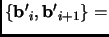 Span
Span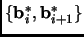 , we find that
, we find that
Therefore,
Now, since
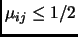 , the projection of
, the projection of
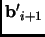 onto
onto
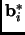 is prevented from being very large.
The calculation follows.
is prevented from being very large.
The calculation follows.
so
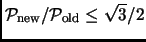 .
.
We see now that we could replace the second Lovász condition by:
- (
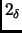 )
)
-
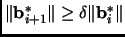 ,
,
where 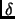 is allowed to be any number such that
is allowed to be any number such that
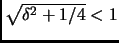 ,
so
,
so
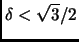 . The running time and quality of the output would
be expected to be greater for larger values of
. The running time and quality of the output would
be expected to be greater for larger values of 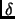 .
.
Remark 1.1
These are the values of
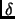
for which we know the algorithm
terminates (and specifically in polynomial time).
However, it is possible for the algorithm to terminate for special
inputs and larger values of
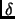
. (For example, an orthogonal basis
and any
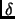
would produce an algorithm that terminates.)
Remark 1.2
Odlyzko and TeRiele used this algorithm to approximate 70 zeroes of the
Riemann Zeta function. In their experiments, the lattice reduction
algorithm terminated rather quickly even in the case
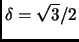
, even though in this case we cannot prove
termination, let alone termination in polynomial time.
Moreover, this large value of
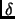
produced outputs
of far higher quality than predicted by the analysis.
This is a case in which the search for a polynomial-time algorithm
required an insight into the nature of the problem, and that insight
lead to a solution that turned out to be ``unreasonably effective''
in practice.



Next: Linear programming
Up: Discrete Math, Eleventh Problem
Previous: Discrete Math, Eleventh Problem
Varsha Dani
2003-07-25
![]() for a lattice is Lovász-reduced if it satisfies the relations:
for a lattice is Lovász-reduced if it satisfies the relations:
![]() .
Because of this, and the fact that
.
Because of this, and the fact that
![]() is a positive integer,
we know that the algorithm must terminate in a number of rounds
logarithmic in the initial potential.
is a positive integer,
we know that the algorithm must terminate in a number of rounds
logarithmic in the initial potential.
![]()
![]() to
to
![]() without affecting the orthogonalized sequence and therefore
without affecting the potential function. Once ``coefficient
reduction'' has been performed,
we check the second property. If there is some
without affecting the orthogonalized sequence and therefore
without affecting the potential function. Once ``coefficient
reduction'' has been performed,
we check the second property. If there is some ![]() with
with
![]() ,
we simply swap these two elements.
This will change the orthogonalized vectors
,
we simply swap these two elements.
This will change the orthogonalized vectors
![]() and
and
![]() , but the potential is only affected by:
, but the potential is only affected by: