Next: About this document ...
Up: Discrete Math, Eleventh Problem
Previous: Linear programming
The objective of primality testing is to take as input
a positive integer, and return as output a verdict
whether the number is prime or composite. Only as recently
as 2002 was it shown that this age-old problem can be solved
in polynomial time; the algorithm was discovered by
Manindra Agarwal, Neeraj Kayal, and Nitin Saxena
(professor and two graduate students)
at the Indian Institute of Technology, Kanpur.
Euclid used the sieve of Eratosthenes to perform
primality testing. In this method, one constructs a
list of the integers from 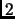 to
to 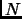 . From this list,
we remove all of the multiples of 2 on the first step.
Since 3 is the smalles remaining number, it must be
prime. We next remove all multiples of 3. Now
5 is the smallest number remaining, so it is
prime. Remove all its multiples.
. From this list,
we remove all of the multiples of 2 on the first step.
Since 3 is the smalles remaining number, it must be
prime. We next remove all multiples of 3. Now
5 is the smallest number remaining, so it is
prime. Remove all its multiples.
Remark 3.1
In order to discover all primes less than
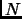
, it is
necessary to continue this process for all primes less
than
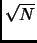
(why?). Therefore, if
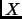
is a number
with
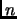
digits,
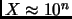
, then it is necessary to
sieve until
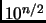
- an exponentially long process.
If we know the primes up to 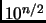 , then we need
only
, then we need
only
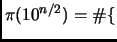 primes
primes 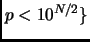 trial divisions. How much of a savings is this?
To estimate this, we need the celebrated
trial divisions. How much of a savings is this?
To estimate this, we need the celebrated
Theorem 3.2 (Prime Number Theorem)
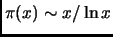
.
Remark 3.3
The error in this approximation is
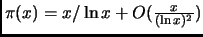
.
Remark 3.4
A better approximation is
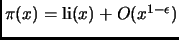
for some constant
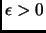
, where
This expression as a good approximation of
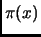
was conjectured by Gauss.
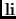
is called the
logarithmic integral.
Remark 3.5
It is believed - and in fact is equivalent to the Riemann Hypothesis -
that the error in the logarithmic integral expression is
of the order of
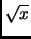
:
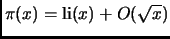
.
Remark 3.6
With regard to the sieve of Eratosthenes, notice that
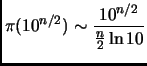
,
which for large enough
, is larger than
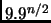
.
Thus we still have exponential complexity.
We shall present two randomized (``Monte Carlo'') algorithms.
These algorithms have two possible outputs:
- ``Composite'' with a proof of compositeness.
- ``Prime.''
In case ``Composite'' is returned, we know that the
number is composite, because a proof of compositeness
is produced. However, in the case the output is ``Prime,''
this is only a guess. It is possible, although
unlikely, that on composite input, the algorithm returns
``prime.'' The probability of this happening is less than
a predetermined
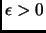 , and it is not
unreasonable to ask
, and it is not
unreasonable to ask 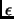 to be less than
to be less than
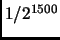 , which error is less than
, which error is less than
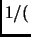 number of particles in the
known universe
number of particles in the
known universe .
.
Remark 3.7
It is often said that a number
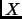
deemed to be prime through
this process is ``very likely prime.'' This statement, however,
does not make sense.
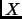
is not chosen at random, it is
given explicitly. Therefore either
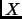
is prime, or it is not,
it cannot have a probability of being prime. Our verdict,
however, is probabilistic; with certain probability we say
``
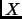
is prime'' and otherwise we say ``
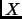
is composite.''
If
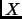
is prime, we shall always say so, so in this case the
chance that we make an error is zero. If
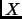
is composite,
then we may accidentally declare that
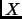
is prime, but
the probability of this happening is
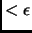
. So overall,
the probability that our verdict is in error is
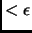
.
Our first tool is Fermat's little Theorem.
Theorem 3.8 (Fermat's little theorem)
If
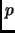
is a prime, and
gcd
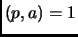
, then
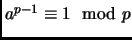
.
Definition 3.9
A
Fermat witness of compositeness of
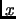
is a number
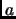
such that
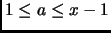
such that
-
gcd
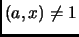 , or
, or
-
gcd
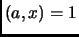 and
and
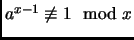 .
.
Remark 3.10
Notice that in the second case, we do not find any factor of
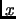
though we do have a proof that it is composite
using the contrapositve of Fermat's little theorem.
Unfortunately, this won't quite work as a basis for a
primality test, because of the following:
Definition 3.11
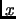
is a
Carmichael number if
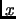
is odd, not prime,
but for all
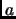
with
gcd
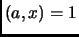
,
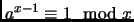
.
Carmichael numbers are rare, but it has been proved
recently that there are infinitely many of them
(Alford, Granville, Pomerance, 1994).
Exercise 3.12
Show that if
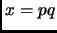
is the product of two primes,
then
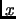
is not a Carmichael number.
Exercise 3.13
Prove that
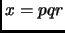
is a Carmichael number if and only
if
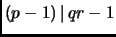
,
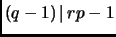
, and
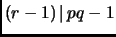
.
Exercise 3.14
Show that the following numbers are Carmichael:
561 (
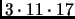
), 1105 (
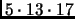
),
1729 (
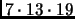
), 2465 (
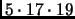
),
2821 (
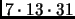
), 6601 (
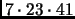
),
8911 (
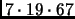
), 10585 (
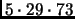
).
(Note: these are the eight smallest Carmichael numbers.)
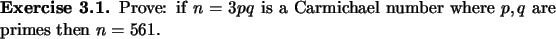
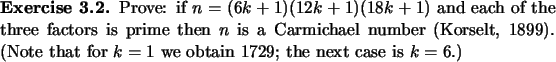

The next exercise shows how to find a witness of compositeness
if the input number is not Carmichael.
Exercise 3.15
Prove that if
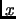
is composite and not Carmichael,
then the probability that a random
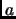
is a Fermat witness is at least
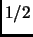
.



Next: About this document ...
Up: Discrete Math, Eleventh Problem
Previous: Linear programming
Varsha Dani
2003-07-25
![]() to
to ![]() . From this list,
we remove all of the multiples of 2 on the first step.
Since 3 is the smalles remaining number, it must be
prime. We next remove all multiples of 3. Now
5 is the smallest number remaining, so it is
prime. Remove all its multiples.
. From this list,
we remove all of the multiples of 2 on the first step.
Since 3 is the smalles remaining number, it must be
prime. We next remove all multiples of 3. Now
5 is the smallest number remaining, so it is
prime. Remove all its multiples.
![]() , then we need
only
, then we need
only
![]() primes
primes ![]() trial divisions. How much of a savings is this?
To estimate this, we need the celebrated
trial divisions. How much of a savings is this?
To estimate this, we need the celebrated
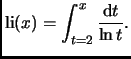
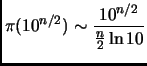 ,
,![]() , and it is not
unreasonable to ask
, and it is not
unreasonable to ask ![]() to be less than
to be less than
![]() , which error is less than
, which error is less than
![]() number of particles in the
known universe
number of particles in the
known universe![]() .
.
![]()