


Next: Rabin-Miller primality testing algorithm
Up: Discrete Math, Thirteenth Problem
Previous: Discrete Math, Thirteenth Problem
Let
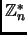 be the set of integers
be the set of integers
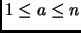 such
that
such
that
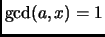 . Recall that the Euler
phi function is defined by
. Recall that the Euler
phi function is defined by
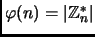 .
.
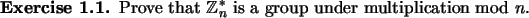
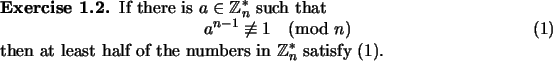
Definition 1.1
Let
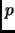
be an odd prime. For
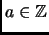
, the
Legendre symbol
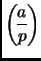
is defined as follows.
In the second case we say that
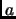
is a
quadratic residue
mod 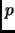
; in the third case,
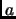
is a
nonresidue mod 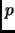
.
Note that 0 is
not a quadratic residue even though
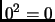
.
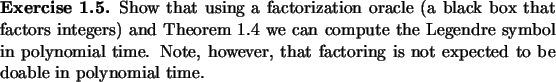
Definition 1.3
Let
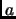
be an integer and
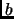
be an odd integer. Let
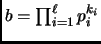
be the factorization
of
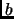
. The Jacobi symbol
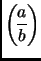
is defined
as follows.
where the right hand side of the definition uses the Legendre
symbol.
Recall that Euclid's algorithm computes the greatest
common divisor of integers 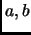 , using
, using
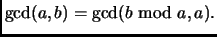 |
(1) |
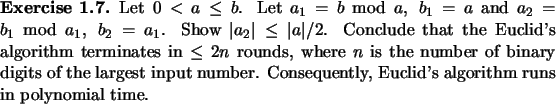
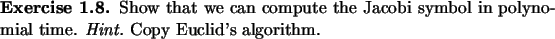
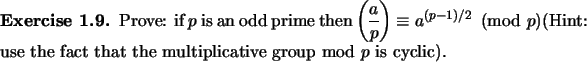
Theorem 1.4
Let
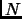
be an integer. Assume that
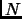
is not a prime and
that
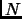
is not
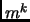
for some
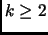
. Then there
exists
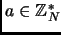
such that
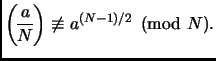 |
(2) |
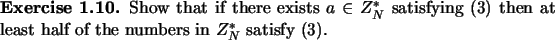
Theorem 1.13, and Exercises 1.11,
1.12, 1.14, 1.15 give us a
polynomial-time randomized algorithm which on input 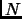 ,
,
- if
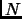 is composite
is composite
- with probability
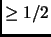 outputs a proof
that
outputs a proof
that 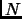 is composite,
is composite,
- otherwise outputs "don't know";
- if
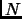 is prime, always outputs "don't know."
is prime, always outputs "don't know."
Amplification. Note that by repeating this algorithm 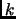 times with
independent coin flips, the probability that we never
find a proof of compositeness when
times with
independent coin flips, the probability that we never
find a proof of compositeness when 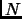 is composite
is reduced to
is composite
is reduced to 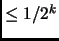 , so if we get
``don't know'' each time, it is a safe bet that
, so if we get
``don't know'' each time, it is a safe bet that
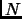 is prime. (How safe?)
is prime. (How safe?)



Next: Rabin-Miller primality testing algorithm
Up: Discrete Math, Thirteenth Problem
Previous: Discrete Math, Thirteenth Problem
Varsha Dani
2003-07-25
![]() be the set of integers
be the set of integers
![]() such
that
such
that
![]() . Recall that the Euler
phi function is defined by
. Recall that the Euler
phi function is defined by
![]() .
.
![]()
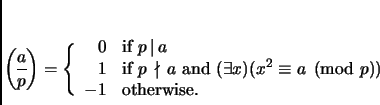
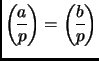 .
.
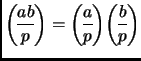 ;
;
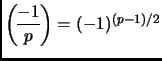 ;
;
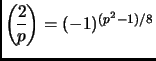 ;
;
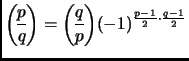 (this identity, observed by Euler
and Legendre and proved by Gauss,
is called Quadratic Reciprocity);
(this identity, observed by Euler
and Legendre and proved by Gauss,
is called Quadratic Reciprocity);
![]()
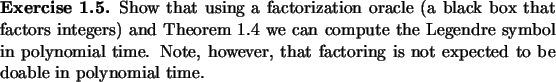
![]()
![]() , using
, using
![]() ,
,
![]() times with
independent coin flips, the probability that we never
find a proof of compositeness when
times with
independent coin flips, the probability that we never
find a proof of compositeness when ![]() is composite
is reduced to
is composite
is reduced to ![]() , so if we get
``don't know'' each time, it is a safe bet that
, so if we get
``don't know'' each time, it is a safe bet that
![]() is prime. (How safe?)
is prime. (How safe?)