


Next: Factoring of integers
Up: Discrete Math, Fourteenth Problem
Previous: Discrete Math, Fourteenth Problem
For the primality test we need to compute
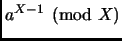 .
There are two problems with the straightforward method
(multiplying
.
There are two problems with the straightforward method
(multiplying 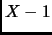 copies of
copies of 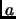 and reducing modulo
and reducing modulo 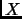 ). First,
the resulting number
). First,
the resulting number 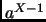 has exponentially many digits
(nearly
has exponentially many digits
(nearly 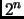 binary digits if
binary digits if 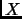 has
has 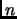 binary digits
and
binary digits
and  ). The space requirement can be reduced to
linear in the bit-length of the input
by doing all operations modulo
). The space requirement can be reduced to
linear in the bit-length of the input
by doing all operations modulo 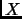 . Second, an
exponential number of modular multiplications is needed, namely
. Second, an
exponential number of modular multiplications is needed, namely
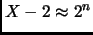 . We can reduce this number to
. We can reduce this number to 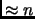 by
``repeated squaring'' - see the ``Pseudocodes for basic
algorithms in Number Theory'' handout.
by
``repeated squaring'' - see the ``Pseudocodes for basic
algorithms in Number Theory'' handout.
Varsha Dani
2003-07-25