In this section we describe the Rabin-Shallit polynomial-time
Las Vegas algorithm to represent a given prime of the form ![]() as the sum of two squares.
as the sum of two squares.
We know that ![]() is a quadratic residue in
is a quadratic residue in
![]() for
for
![]() ,
i.e. there exists
,
i.e. there exists ![]() such that
such that
![]() . Our first task
is to find such
. Our first task
is to find such ![]() ? This is equivalent to factoring the polynomial
? This is equivalent to factoring the polynomial
![]() .
.
Divisibility, primes, g.c.d. are defined among Gaussian integers the same way as among integers. (Recall: by definition, the greatest common divisor is not ``largest'' among the common divisors but one that is a common multiple of all common divisors. So its existence is not evident.)
There are four units (numbers dividing ![]() ) among Gaussian integers,
) among Gaussian integers,
![]() , and
, and ![]() .
Let us take a look at Gaussian primes.
.
Let us take a look at Gaussian primes. ![]() and
and ![]() are not primes in
are not primes in
![]() (because
(because
![]() ) but
) but ![]() remains a prime.
remains a prime.
![]()
![]()
![]()
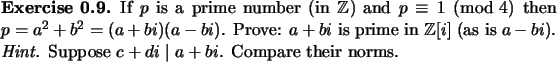
![\begin{exercise}
% latex2html id marker 935Prove that Euclid's algorithm works...
...nation
of $z$\ and $w$\ with coefficients from ${\mathbb{Z}}[i]$.
\end{exercise}](img83.gif)
The algorithm
Let
![]() . By factoring the polynomial
. By factoring the polynomial ![]() over
over
![]() , we found, in Las Vegas polynomial time,
and integer
, we found, in Las Vegas polynomial time,
and integer ![]() such that
such that
![]() .
Now
.
Now
![]() . Since
. Since ![]() (
(![]() ,
, ![]() unknown)
and
unknown)
and ![]() is a prime in
is a prime in
![]() , it follows that
, it follows that
![]() divides either
divides either ![]() or
or ![]() (but not both - why?).
Therefore
(but not both - why?).
Therefore ![]() splits
splits ![]() : if
: if
![]() then
then
![]() .
Otherwise,
.
Otherwise,
![]() . In either case, we find
. In either case, we find ![]() using Euclid's algorithm in
using Euclid's algorithm in
![]() .
.
