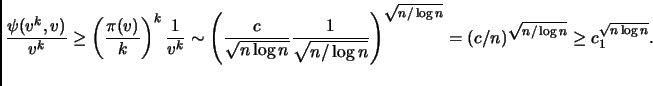J. Dixon was the first to show that ![]() -digit integers can be factored in
-digit integers can be factored in
![]() steps. Let
steps. Let ![]() be an
be an ![]() -digit integer
(
-digit integer
(
![]() ) which we want to factor.
) which we want to factor.
Suppose we can find ![]() such that
such that
![]() and
and
![]() .
Then
.
Then ![]() divides
divides
![]() and
and ![]() splits
splits ![]() .
.
![]()
How do we find such ![]() and
and ![]() ?
Let
?
Let ![]() be a threshold number
be a threshold number
![]() and let
and let
![]() .
Let
.
Let
![]() be a random number.
Let
be a random number.
Let
![]() . If
. If ![]() is not
is not
![]() -smooth, discard it and try again. Let
-smooth, discard it and try again. Let ![]() .
Keep generating the
.
Keep generating the ![]() until
until ![]() smooth numbers
smooth numbers ![]() are found.
are found.
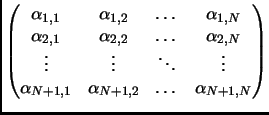
Suppose
![]() where
where
![]() .
.
Consider the matrix
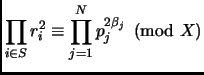
There are two catches in this sketch. First, the smooth numbers
have to happen sufficiently frequently. Second, the probability of
![]() must be significant.
must be significant.
The second claim seems more plausible and can be proven by using a clever counting argument. Here we present intuition behind the first claim.
Let ![]() be the number of
be the number of ![]() -smooth numbers less than
-smooth numbers less than ![]() .
Let
.
Let
![]() , i.e.
, i.e.
![]() .
Clearly,
.
Clearly,
![]() (the product of any
(the product of any ![]() primes
primes ![]() is smooth).
What is the probability that a random number is smooth?
is smooth).
What is the probability that a random number is smooth?