


Next: Linear Algebra
Up: Discrete Math, Second Problem
Previous: Discrete Math, Second Problem
Remark 1.1
For an arithmetic progression,
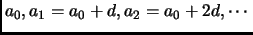
to have infinitely many primes, it is necessary that
gcd
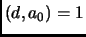
.
This is true because the gcd will divide all terms. The converse is also true:
Theorem 1.2
(Dirichlet)
Whenever
gcd
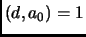
, the arithmetic progression,
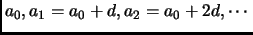
will have infinitely many primes.
This remarkable theorem is proved using complex analysis. We shall give
elementary proofs of special cases. The case 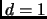 is simply the
infinitude of primes.
is simply the
infinitude of primes.
Theorem 1.3
(Euclid)
There are infinitely many primes.
Proof.
For a contradiction, assume there are finitely many,
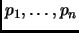
. Construct
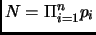
. Then for any
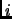
,
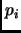
does not divide
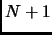
, so
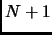
is not divisible by any prime. This is a contradiction, since all numbers
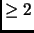
are divisible by some prime. (This can be easily proved by induction.)

Definition 1.4
We say that two numbers,
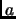
, and
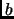
are
congruent mod m, or
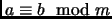
if
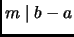
.
Lemma 1.5
If
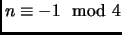
, then it must have a prime divisor
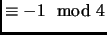
.
Proof.
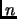
is an odd number. Thus it is the product of odd primes. If all of these primes are
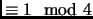
, then their product is also
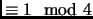
, which is a contradiction.

Theorem 1.6
There are infinitely many primes
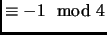
.
Proof.
Assume that there are finitely many,
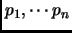
. Construct
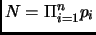
. Then by the Lemma,
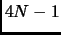
must have a prime divisor congruent to
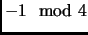
. However, this is a contradiction, since no
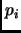
divides it (why?).

The infinitude of primes
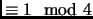 is not so straightforward.
We need the following
is not so straightforward.
We need the following
Theorem 1.8
There are infinitely many primes congruent to
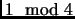
.
Proof.
Assume that there are finitely many,
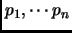
. Construct
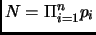
. Then, by the Lemma, all (odd) prime divisors of
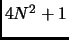
must be congruent to
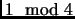
. This is a contradiction, since this number is not divisible by any of the
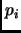
. (Why did we multiply by 4?)

We need to prove the Lemma. This, in turn, requires Fermat's Little
Theorem, which we now state.
Exercise 1.10
Show that each of the last three statements is equivalent to the first.
Proof.
We may, (by adding a multiple of
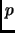
to
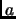
) assume that
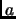
is positive. Now consider all strings of length
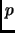
of numbers between
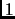
and
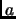
. For example, if
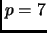
,
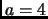
, we could have
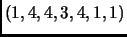
. There are
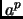
such strings. Call two strings equivalent if ``they make the same necklace,'' i.e., they differ by cyclic rotation. That is, the above string is equivalent to
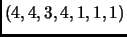
,
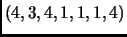
,
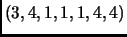
, etc. Now in most cases, there will be exactly
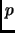
equivalent strings. The exceptions are the strings
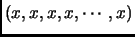
, which will have only one string (themselves) in their equivalence class. Therefore the number of equivalence classes (``necklaces'') is
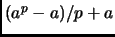
, so
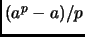
must be an integer.

Definition 1.11
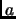
is a
quadratic residue modulo the prime
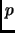
if
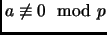
and there exists an
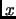
such that
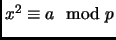
.
Proof of Lemma 1.7.
The condition is that
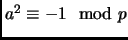 ; and by Fermat's Little Theorem
we have
; and by Fermat's Little Theorem
we have
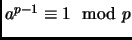 . Since
. Since 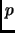 is odd,
is odd,
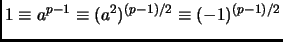 . Now since
. Now since 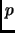 is odd,
is odd,
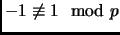 , so
, so 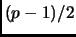 must be even, or
must be even, or
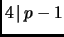 .
.

Exercise 1.12
Prove: every prime greater than 3 is congruent to
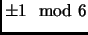
.
Exercise 1.13
There are infinitely many primes of the form
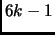
.
Hint. Follow the
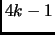
case.
Exercise 1.14
There are infinitely many primes of the form
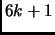
.
This is harder; you need a new lemma:
Exercise 1.15
If
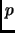
is a prime and
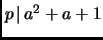
, then
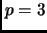
or
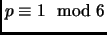
.
Hint. Prove:
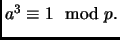
Definition 1.16
If
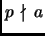
, the
order of 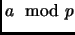
is the smallest positive integer
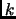
, such that
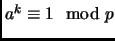
. We say
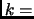
ord
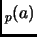
.
Exercise 1.17
Prove that the following statement is equivalent
to Fermat's Little Theorem,
1.9.
- If
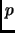 is a prime and
is a prime and
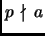 , then
ord
, then
ord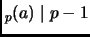 .
.
Exercise 1.18
If
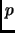
is a prime number other than 2 or 5 then the decimal expansion
of
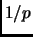
is periodic with period
ord
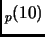
.
Definition 1.19
We say that
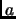
is a
primitive root modulo 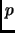
if
ord
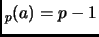
.
Exercise 1.20
10 is a primitive root mod 7 if and only if 3 is a primitive root mod 7.
Exercise 1.21
Verify:
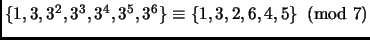
, so that all numbers from 1 to 6 appear before repetition occurs in the sequence
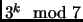
.
Exercise 1.22
Prove:
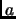
is a primitive root mod
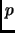
if and only if the set
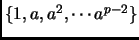
represents all numbers numbers modulo
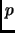
that are not divisible by
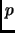
.
Theorem 1.23
For every prime,
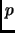
, there exists a primitive root mod
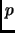
.
(We shall prove this important result later and will not use it in this set of exercises.)
Our next goal is to prove the following remarkable result:
Theorem 1.24 (Gauss)
A prime number
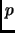
can be written as a sum of two squares if and
only if
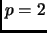
or
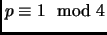
.
The ``only if'' part is straightforward:
Exercise 1.25
If
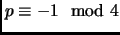
, then
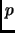
cannot be written as the sum of two squares.
Hint. Observe that
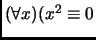
or

.
To prove the converse, we need to learn about polynomials,
quadratic residues, and lattices.
Theorem 1.26
Assume
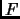
is a field. If
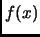
is a polynomial over
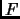
then
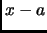
is a divisor of
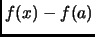
.
Proof.
Let
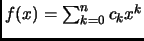
. Since
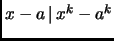
, and
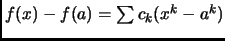
, we see that
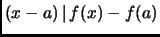
,

Notation 1.27
![$ F[x]$](img84.gif)
is the ring of all polynomials over
.
Corollary 1.28
If
![$ f\in F[x]$](img85.gif)
, and
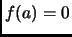
, then
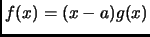
for some
![$ g\in F[x]$](img88.gif)
.
Proof.
By induction on
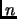
.

Proof.
We already proved that (b)
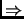
(a) (Lemma
1.7).
For the other direction, assume now that
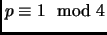
.
Let
![$ f(x)=x^p-x\in\mathbb{F}_p[x]$](img91.gif)
.
By Fermat's Little Theorem, every element of
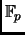
is a root of
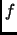
.
We factor
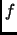
as
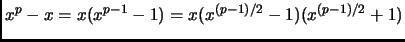
.
Since none of the factors has more roots than its degree and
the total number of roots is
, each factor must have exactly as many
roots as its degree. In particular, there must exist a root
of
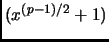
.
However, since
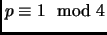
,
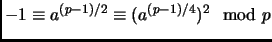
. Therefore
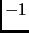
is a square mod
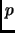
.

Definition 1.31
A lattice in
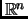
is a set
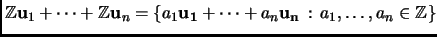
, where
is linearly independent over
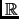
.
Definition 1.32
The set
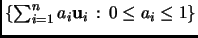
is a
fundamental parallelepiped of the lattice
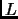
.
Our main interest in this section will be the two-dimensional case,
so instead of the 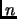 -dimensional parallelepipeds the reader may
think of the familiar parallelograms in the plane.
-dimensional parallelepipeds the reader may
think of the familiar parallelograms in the plane.
Exercise 1.33
The translates of the fundamental parallelepiped by vectors
in
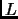
tile
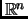
, i.e., they cover
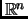
without overlapping interiors.
Theorem 1.34
A fundamental parallelepiped is characterized by the fact that it is a
parallelepiped which intersects the lattice in exactly its
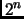
corners.
Recall that the area of a parallelogram spanned by
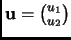 and
and
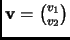 is
is
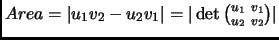 . (The analogous determinant expression works in
. (The analogous determinant expression works in  -dimensions.)
-dimensions.)
Exercise 1.35
All fundamental parallelepipeds have the same area.
Definition 1.36
A subset
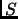
of a real vector space
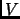
, is called
convex if for each
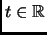
,
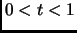
, and each
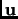
,
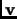
in
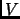
,
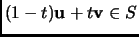
.
Theorem 1.37 (Minkowski)
Let
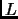
be a lattice in
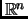
, and the area of a findamental parallelogram be
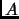
. If
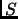
is convex, centrally symmetric about the origin, and the area of
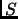
is greater than
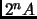
, then
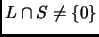
.
(The proof of this fundamental result in the ``Geometry of Numbers''
will be given later.) Next we use Minkowski's Theorem to prove Gauss'
result, 1.24. The devilishly clever proof is due to
Paul Turán.
Theorem 1.38
If
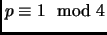
, then there are integers,
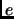
, and
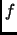
, such that
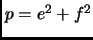
.
Proof.
By Theorem
1.30, there exists a
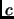
such that
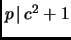
. Let
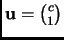
and
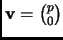
be vectors in
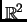
. A general point in the lattice,
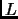
spanned by these is
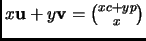
. Note that
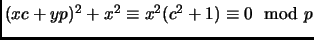
, so if
is in
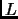
, then
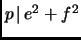
. Look at the open disk:
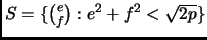
. The area of
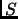
is
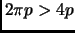
, and the area of the fundamental parallelogram is
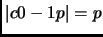
, so by Minkowski's Theorem,
1.37, there is some nonzero point in the lattice and in the disk. Therefore, there exist
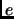
and
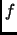
such that
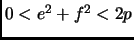
, and
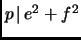
, so
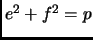
.

Divisor game.
Consider the following game, played by two people: Choose a number 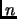 . Players take turns naming a factor of
. Players take turns naming a factor of 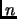 . Once a factor is named, it and none of its factors may be named again. The loser is the first player to say
. Once a factor is named, it and none of its factors may be named again. The loser is the first player to say 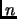 .
.
Exercise 1.39
Find the winning strategies for the first player when
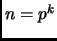
,
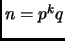
,
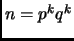
,
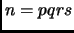
.
Exercise 1.40
Show that the first player always has a winning strategy.
Hint. Do not try to find the winning strategy for all
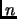
.
Coin placing game.
Given a rectangular table and an unlimited supply of quarters, each player takes turns placing quarters on the table (this is a ``continuous'' game). The quarters, once placed, may not be moved; they may not overlap, and may not hang over the edge.
Exercise 1.41
Find a winning strategy for the first player.



Next: Linear Algebra
Up: Discrete Math, Second Problem
Previous: Discrete Math, Second Problem
Varsha Dani
2003-07-25
![]() ; and by Fermat's Little Theorem
we have
; and by Fermat's Little Theorem
we have
![]() . Since
. Since ![]() is odd,
is odd,
![]() . Now since
. Now since ![]() is odd,
is odd,
![]() , so
, so ![]() must be even, or
must be even, or
![]() .
.
![]()
![]() -dimensional parallelepipeds the reader may
think of the familiar parallelograms in the plane.
-dimensional parallelepipeds the reader may
think of the familiar parallelograms in the plane.
![]() and
and
![]() is
is
![]() . (The analogous determinant expression works in
. (The analogous determinant expression works in ![]() -dimensions.)
-dimensions.)
![]() . Players take turns naming a factor of
. Players take turns naming a factor of ![]() . Once a factor is named, it and none of its factors may be named again. The loser is the first player to say
. Once a factor is named, it and none of its factors may be named again. The loser is the first player to say ![]() .
.