


Next: About this document ...
Up: Discrete Math, Second Problem
Previous: Number Theory
Let 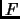 be a field. Note that the ring
be a field. Note that the ring ![$ F[x]$](img84.gif) of univariate polynomials over
of univariate polynomials over 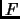 is an infinite-dminesional vector space over
is an infinite-dminesional vector space over 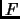 with a nice (standard) basis:
with a nice (standard) basis:
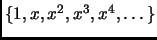 .
.
Example 2.1
Let
![$ F_n[x]$](img139.gif)
denote the set of polynomials of degree
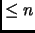
.
This is an
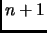
-dimensional subspace of
![$ F[x]$](img84.gif)
. We calculate the
matrix representing the map
![$ \frac{d}{dx}:F_n[x]\to F_n[x]$](img142.gif)
with respect
to the standard basis
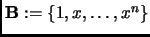
.
Example 2.2
Consider the rotation of the Euclidean plane
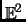
by angle
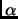
about the origin.
We denote this linear map by
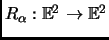
.
Choose as the basis a pair of perpendicular unit vectors
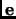
and
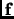
. Then we have that
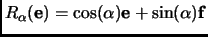
, and
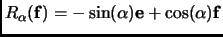
. Therefore the matrix for
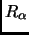
in the basis
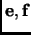
, is
Example 2.3
Consider the reflection of the Euclidean plane
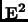
through the line which makes an angle
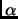
with
horizontal (
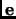
) and passes through the origin.
We denote this linear map by
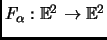
.
Then we have
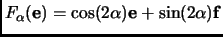
, and
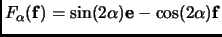
. Therefore the
matrix for
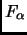
in the basis
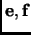
, is
Example 2.4
If in the previous example, we had chosen the basis
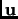
and
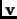
, where
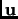
is a vector along the line of reflection, and
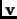
is perpendicular to it, then the matrix for
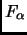
would be:
Definition 2.5
Given a square matrix
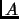
, define
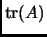
, the
trace of
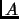
to be the sum of the diagonal entries of
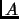
.
Remark 2.6
The following observations are special cases of a
general principle:
-
![% latex2html id marker 3544
$ \mathop{\rm tr}\nolimits ([F_\alpha]_{{\mathbf{e}}...
...athbf{f}}})=0=\mathop{\rm tr}\nolimits ([F_\alpha]_{{\mathbf{u}},{\mathbf{v}}})$](img163.gif) .
.
-
![$ \det([F_\alpha]_{{\mathbf{e}},{\mathbf{f}}})=-1=\det([F_\alpha]_{{\mathbf{u}},{\mathbf{v}}})$](img164.gif) .
.
Definition 2.7
Let
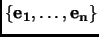
, and
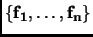
be two bases for a vector space
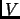
. The basis change transformation
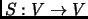
is the unique (invertible) linear map defined by
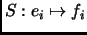
.
Example 2.8
Let
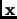
be a vector in
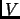
. Then
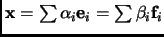
. Notice that
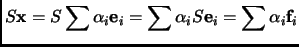
.
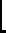
Therefore if
![$ [S{\mathbf{x}}]_{{\mathbf{f}}}=[{\mathbf{x}}]_{\mathbf{e}}$](img174.gif)
. Also,
![$ [S{\mathbf{x}}]_{{\mathbf{f}}}=[S]_{{\mathbf{f}}}[{\mathbf{x}}]_{{\mathbf{f}}}$](img175.gif)
by the following exercise. Thus
![$ [{\mathbf{x}}]_{{\mathbf{f}}}=[S^{-1}]_{{\mathbf{f}}}[{\mathbf{x}}]_{{\mathbf{e}}}$](img176.gif)
Exercise 2.9
Let
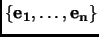
be a basis for
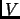
, and let
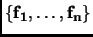
be a basis for
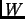
. Let
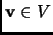
, and let
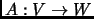
. Show that
![$ [A]_{{\mathbf{e}},{\mathbf{f}}}[{\mathbf{v}}]_{\mathbf{e}}=[A{\mathbf{v}}]_{{\mathbf{f}}}$](img180.gif)
.
Exercise 2.10
Let
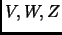
be vector spaces over
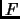
.
Let
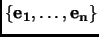
be a basis for
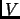
,
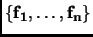
be a basis for
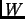
,
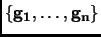
be a basis for
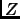
. Let
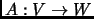
,
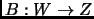
.
Show that
![$ [BA]_{{\mathbf{e}},{\mathbf{g}}}=[B]_{{\mathbf{f}},{\mathbf{g}}}[A]_{{\mathbf{e}},{\mathbf{f}}}$](img185.gif)
.
Exercise 2.11
If
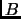
,
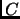
are
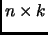
matrices that
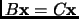
for all
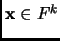
then
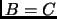
.
Remark 2.12
Let
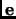
,
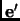
be two bases for
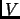
with change of basis map
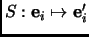
.
Let
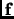
,
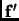
be two bases for
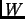
with change of basis map
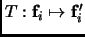
.
Let
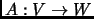
. We want to compare
![$ [A]_{{\mathbf{e}}{\mathbf{f}}}$](img196.gif)
with
![$ [A]_{{\mathbf{e'}}{\mathbf{f'}}}$](img197.gif)
.
Let
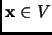
. We have the following identities:
Therefore for all
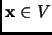
,
However, by the previous exercise, this is only possible if
Remark 2.13
From the previous remark, we deduce that
![$\displaystyle [A]_{{\mathbf{e}}{\mathbf{f}}}=[T]_{{\mathbf{f'}}{\mathbf{f'}}}[A...
...f{f'}}}[S^{-1}]_{{\mathbf{e'}}{\mathbf{e'}}}=[TAS]_{{\mathbf{e'}}{\mathbf{f'}}}$](img204.gif)
.
Corollary 2.14
Let
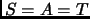
. Then
![$\displaystyle [S]_{{\mathbf{e}}{\mathbf{e}}}=[TAS^{-1}]_{{\mathbf{f}}{\mathbf{f}}}=[S]_{{\mathbf{f}}{\mathbf{f}}}$](img206.gif)
.
Corollary 2.15
If

,
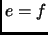
, then
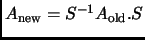
Definition 2.16
Two
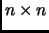
matrices
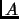
,
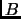
are
similar if there exists some invertible
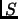
such that
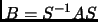
. We write
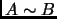
.
Definition 2.17
The
characteristic polynomial 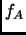
of a matrix
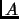
is the determinant
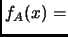
det
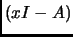
, where
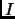
is the
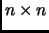
identity matrix.
Exercise 2.18
If
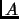
and
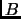
are
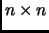
matrices, then
det
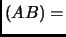
det
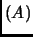
det
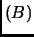
.
Exercise 2.19
If
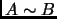
then
det
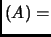
det
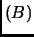
.
Exercise 2.20
If
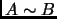
then
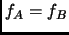
.
Definition 2.21
If
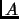
is a matrix, the roots of
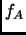
are called the
eigenvalues of
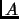
.
Definition 2.22
If
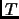
is a linear transformation, then the
characteristic polynomial of
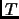
is the characteristic polynomial of a matrix for
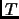
in some basis. The last exercise shows that this is well-defined.
Definition 2.23
If
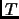
is a linear transformation, then the
eigenvalues of
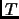
are the roots of the characteristic polynomial.
Remark 2.24
If
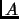
is an upper triangular matrix, then the eigenvalues of
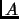
are the diagonal entries of
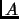
, taken with multiplicity.
Exercise 2.25
Find two
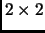
matrices,
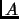
and
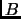
such that
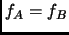
but
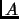
and
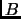
are not similar.
Exercise 2.26
If
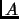
is an
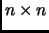
matrix over a field
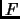
, and
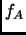
has
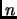
distinct roots in
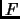
, then
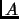
is ``diagonalizable,'' i.e.,
is similar to a diagonal matrix. (What are the entries of this diagonal matrix?)



Next: About this document ...
Up: Discrete Math, Second Problem
Previous: Number Theory
Varsha Dani
2003-07-25
![]() be a field. Note that the ring
be a field. Note that the ring ![]() of univariate polynomials over
of univariate polynomials over ![]() is an infinite-dminesional vector space over
is an infinite-dminesional vector space over ![]() with a nice (standard) basis:
with a nice (standard) basis:
![]() .
.
![\begin{displaymath}
% latex2html id marker 3479\left[\frac{d}{dx}\right]_{{\ma...
...ts & n \\
0 & 0 & 0 & 0 & \ldots & 0 \\
\end{array}\right]
\end{displaymath}](img144.gif)
![\begin{displaymath}
% latex2html id marker 3500[R_\alpha]_{{\mathbf{e}},{\math...
...(\alpha)\\
\sin(\alpha)&\cos(\alpha)\\
\end{array}\right].
\end{displaymath}](img154.gif)
![\begin{displaymath}
% latex2html id marker 3519[F_\alpha]_{{\mathbf{e}},{\math...
...lpha)\\
\sin(2\alpha)&-\cos(2\alpha)\\
\end{array}\right].
\end{displaymath}](img160.gif)
![\begin{displaymath}
% latex2html id marker 3532[F_\alpha]_{{\mathbf{u}},{\math...
...
\begin{array}{rr}
1 & 0 \\
0 & -1 \\
\end{array}\right].
\end{displaymath}](img161.gif)
![\begin{displaymath}
% latex2html id marker 3569[{\mathbf{x}}]_{{\mathbf{e}}}=
...
...rray}{c}
\alpha_1 \\
\vdots \\
\alpha_n
\end{array}\right]
\end{displaymath}](img173.gif)