


Next: Euclidean spaces
Up: Discrete Math, Third Problem
Previous: Number Theory
Example 2.1 (Dissimilar matrices with same characteristic polynomial)
![% latex2html id marker 1851
$\displaystyle A=
\left[ \begin{array}{cc}
1 & 1 \\
0 & 1 \\
\end{array}\right]$](img14.gif)
and
![% latex2html id marker 1852
$\displaystyle B=
\left[\begin{array}{cc}
1 & 0 \\
0 & 1 \\
\end{array}\right]$](img15.gif)
and the characteristic polynomials are
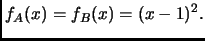
Definition 2.2
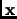
is an
eigenvector to the
geometric eigenvalue 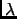
for matrix
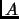
if
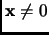
and
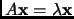
.
An
algebraic eigenvalue of
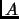
is a root of the characteristic polynomial
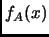
.
Exercise 2.3
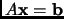
is an inhomogeneous system of equations. Show it has a solution iff
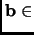
span
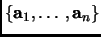
iff rk
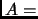
rk
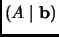
.
Exercise 2.4
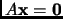
is a homogeneous system of equations. Show it has a nontrivial solution iff columns are linearly dependent.
Determinants - quick and dirty1.
Given an 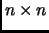 matrix
matrix 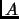 , let
, let 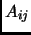 denote the matrix formed by deleting the
denote the matrix formed by deleting the 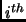 row and
row and 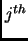 column. The determinat-expansion by the
column. The determinat-expansion by the 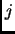 -th column is
-th column is
det
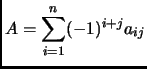
det
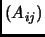
- the choice of
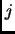
doesn't matter,
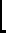
where det
![% latex2html id marker 1903
$\displaystyle \left[\begin{array}{cc}
a & b\\
c & d
\end{array}\right]
=ad-bc.
$](img37.gif)
We could also reverse the roles of 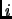 and
and 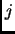 in the above equation.
Switching two rows or two columns changes the sign of the determinant.
Adding some linear combination of rows (or columns)
to another row (or column respectively) does not affect the determinant.
in the above equation.
Switching two rows or two columns changes the sign of the determinant.
Adding some linear combination of rows (or columns)
to another row (or column respectively) does not affect the determinant.
Note that the above rules are rules of calculation, not definition.
It is far from obvious that these rules actually result in a unique number
regardless of the choices made along the way. (What is the definition?)
Theorem 2.5
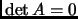
iff the columns are linearly dependent.
Exercise 2.6
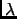
is an eigenvalue of
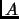
iff
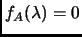
. (In other words the two definitions of eigenvalue are equivalent).
Exercise 2.7
Let
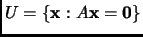
. This is a subspace of
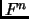
.
Show dim
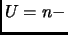
rk
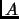
, where by rk
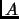
we mean the row rank.
Exercise 2.8
Show that for any matrix the row rank equals the column rank.
Definition 2.9
The
algebraic multiplicity of an eigenvalue is its multiplicity as a root of the characteristic polynomial. The
geometric multiplicity of
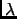
is dim
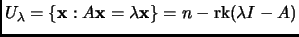
.
Example 2.10
![% latex2html id marker 1937
$\displaystyle \left[ \begin{array}{cc}
1 & 1 \\
0 & 1 \\
\end{array}\right]$](img45.gif)
has eigenvalue 1 with algebraic multiplicity 2 and geometric multiplicity 1
Example 2.11
However if we extend our base field to
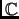
then
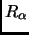
has eigenvectors
Exercise 2.12
Show that over
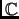
a matrix
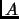
is diagonalizable (i.e., it has an eigenbasis) iff the geometric and algebraic multiplicities of all its eigenvalues coincide.



Next: Euclidean spaces
Up: Discrete Math, Third Problem
Previous: Number Theory
Varsha Dani
2003-07-25
![% latex2html id marker 1851
$\displaystyle A=
\left[ \begin{array}{cc}
1 & 1 \\
0 & 1 \\
\end{array}\right]$](img14.gif) and
and ![% latex2html id marker 1852
$\displaystyle B=
\left[\begin{array}{cc}
1 & 0 \\
0 & 1 \\
\end{array}\right]$](img15.gif) and the characteristic polynomials are
and the characteristic polynomials are ![% latex2html id marker 1851
$\displaystyle A=
\left[ \begin{array}{cc}
1 & 1 \\
0 & 1 \\
\end{array}\right]$](img14.gif) and
and ![% latex2html id marker 1852
$\displaystyle B=
\left[\begin{array}{cc}
1 & 0 \\
0 & 1 \\
\end{array}\right]$](img15.gif) and the characteristic polynomials are
and the characteristic polynomials are ![]() matrix
matrix ![]() , let
, let ![]() denote the matrix formed by deleting the
denote the matrix formed by deleting the ![]() row and
row and ![]() column. The determinat-expansion by the
column. The determinat-expansion by the ![]() -th column is
-th column is
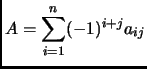 det
det![% latex2html id marker 1903
$\displaystyle \left[\begin{array}{cc}
a & b\\
c & d
\end{array}\right]
=ad-bc.
$](img37.gif)
![]() and
and ![]() in the above equation.
Switching two rows or two columns changes the sign of the determinant.
Adding some linear combination of rows (or columns)
to another row (or column respectively) does not affect the determinant.
in the above equation.
Switching two rows or two columns changes the sign of the determinant.
Adding some linear combination of rows (or columns)
to another row (or column respectively) does not affect the determinant.
![% latex2html id marker 1937
$\displaystyle \left[ \begin{array}{cc}
1 & 1 \\
0 & 1 \\
\end{array}\right]$](img45.gif) has eigenvalue 1 with algebraic multiplicity 2 and geometric multiplicity 1
has eigenvalue 1 with algebraic multiplicity 2 and geometric multiplicity 1![% latex2html id marker 1941
$\displaystyle R_\alpha=\left[\begin{array}{cc}
\cos\alpha & -\sin\alpha\\
\sin\alpha & \cos\alpha
\end{array}\right]$](img47.gif) is a matrix with no eigenvalues over
is a matrix with no eigenvalues over ![% latex2html id marker 1950
$\displaystyle \left[\begin{array}{c}
i\\
1
\end{array}\right]$](img52.gif) and
and ![% latex2html id marker 1951
$\displaystyle \left[\begin{array}{c}
-i\\
1
\end{array}\right]$](img53.gif) and eigenvalues
and eigenvalues