


Next: About this document ...
Up: Discrete Math, Third Problem
Previous: Euclidean spaces
Exercise 4.1
An
isometry is a linear isomorphism
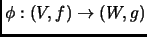
such that
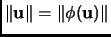
for all

. Show
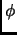
is an isometry iff
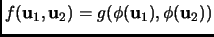
for all vectors
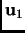
and
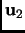
in
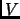
.
Exercise 4.2
Show
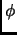
is an isometry iff it maps an orthonormal basis to an orthonormal basis.
Theorem 4.3
![$ f({\mathbf{u}},{\mathbf{v}})=[{\mathbf{u}}]^*_{\underline{e}}[{\mathbf{v}}]_{\underline{e}}=\overline{u}_1v_1+\cdots+\overline{u}_nv_n$](img93.gif)
where
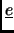
is an orthonormal basis.
Exercise 4.4
Show that
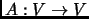
is an isometry iff the columns of
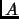
form an orthonormal basis of
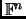
, where
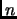
is the dimension of
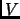
.
Exercise 4.5
Show
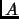
is an isometry iff
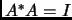
iff
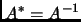
iff
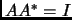
. Such a matrix is called
unitary.
Example 4.6
Unitary matrices living in real vector spaces are known as
orthogonal matrices. The rotations and reflections of last lecture are examples under the standard inner product on
.
When are diagonal matrices unitary?
If and only if 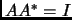 iff
iff
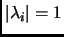 for all
for all 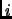 iff all eigenvalues have unit length.
iff all eigenvalues have unit length.
Definition 4.7
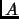
and
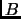
are
similar under unitary transforms, denoted
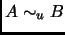
, if there exists a unitary matrix
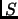
such that
Theorem 4.8
(Spectral Theorem)
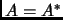
if and only if
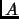
is similar under unitary transforms to



Next: About this document ...
Up: Discrete Math, Third Problem
Previous: Euclidean spaces
Varsha Dani
2003-07-25
![]() iff
iff
![]() for all
for all ![]() iff all eigenvalues have unit length.
iff all eigenvalues have unit length.
![\begin{displaymath}
% latex2html id marker 2123\left[
\begin{array}{ccc}
\lamb...
...{array}\right]\mbox{ with the } \lambda_i\mbox{ real numbers.}
\end{displaymath}](img107.gif)