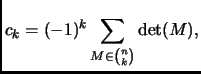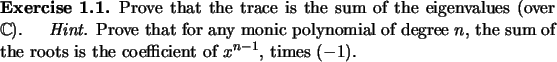Linear Algebra

Remark 1.1   Recall that if we have a polynomial over $\mathbb{Z}$, $f(x)=a_nx^n+\cdots+a_0$, and a rational root $p/q$ with gcd$(p,q)=1$, then $p{\,\mid\,}a_0$, and $q{\,\mid\,}a_n$.

Theorem 1.2   If $A$ is an $n\times k$ matrix, and $B$ is a $k\times n$ matrix, then Tr$(AB)=$Tr$(BA)$.

Corollary 1.3   If $A$ and $B$ are $n\times n$ matrices, and $A\sim B$, then Tr$(A)=$Tr$(B)$.

Proof. Tr$(B)=$Tr$((S^{-1}A)S)=$Tr$(S(S^{-1}A))=$Tr$(A).$ $\qedsymbol$

We may also prove this by considering the characteristic polynomial of $A$. Let
$f_A(x)=x^n+c_{n-1}x^{n-1}+\cdots+c_0$. Then $c_{n-1}=-$Tr$(A)$, $c_{0}=(-1)^n\det(A)$, and generally:

$$c_k=(-1)^k\sum_{M\in\binom{n}{k}}\det(M),$$

where the sum is over all $k\times k$ symmetric minors of $A$. A symmetric minor is a submatrix symmetrically positioned with respect to the main diagonal, i.e., it has the same row numbers and column numbers. Since the characteristic polynomial is preserved under similarity, all such expressions are preserved, so specifically, the traces of similar matrices are equal.

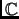
Remark 1.4   Recall that every matrix over $\mathbb{C}$ is similar to an upper triangular matrix, and the diagonal entries of an upper triangular matrix are its eigenvalues. This gives an alternative proof of the fact that the trace of a square matrix is the sum of its eigenvalues.