An Extremal Problem in Discrete Geometry

Definition 0.6   A set $S\subseteq{\mathbb{R}}^n$ is called a 2-distance set if there exist $\alpha,\beta\in{\mathbb{R}}$ such that $(\forall x,y\in S) (x\neq y \Rightarrow {\mathrm {dist}}(x,y)\in\{\alpha,\beta\})$.

Example 0.7   In the plane a regular pentagon is a 2-distance set. In 3D, an octahedron (dual of the cube) is a 2-distance set.

Example 0.8   Some examples of 2-distance sets in ${\mathbb{R}}^n$:

• Set of size $n$: standard orthonormal basis (vectors ${\mathbf{e}}_i$),
• Set of size $2n$: hyper-octahedron (vectors $\pm {\mathbf{e}}_i$),
• Set of size $\binom{n}{2}$: vectors ${\mathbf{e}}_i+{\mathbf{e}}_j$ for $i\neq j$.

The following theorem shows that this example is asymptotically optimal.

Theorem 0.9 (Larman,Rogers,Seidel)   Let $m(n)$ be the maximum size of a 2-distance set in ${\mathbb{R}}^n$. Then

$$m(n)\leq \frac{(n+1)(n+4)}{2}$$

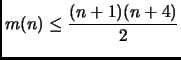
The proof of this theorem is an application of the ``linear algebra method:'' associate $m$ vectors from some space $V$ with our $m$ objects in such a way that the constraints on our objects imply that the vectors associated will be linearly independent. Then it will follow that $m\le\dim(V)$. Choose $V$ such that $\dim(V)$ will be the desired bound (in this case, $(n+1)(n+4)/2$).

The trick, of course, is to find the right space $V$ and the way of matching our objects to vectors in $V$ so that the constraints translate into linear independence.

Our space $V$ will be a space of multivariate polynomials; the trick goes back to a paper by Koornwinder.

A complete proof can be found in the ``blue book'' by Babai and Frankl, page 13.