
Instructor: Laszlo Babai
Scribe: Varsha Dani
![]()
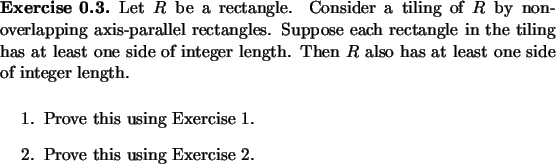
We now turn our attention to an algorithmic problem. Consider a lattice in
![]() , specified by a basis. We want to find the shortest non-zero vector
in the lattice. Moreover, we would like to be able to do this ``efficiently,''
in the sense that the number of steps taken by the algorithm should
be bounded by a polynomial function of the bit-length of the input
(number of zeros and ones needed to describe the input).
, specified by a basis. We want to find the shortest non-zero vector
in the lattice. Moreover, we would like to be able to do this ``efficiently,''
in the sense that the number of steps taken by the algorithm should
be bounded by a polynomial function of the bit-length of the input
(number of zeros and ones needed to describe the input).
Let
![]() where the
where the
![]() are linearly
independent. Note that we restrict our attention to bases in
are linearly
independent. Note that we restrict our attention to bases in
![]() rather
than
rather
than
![]() because we need the number of bits in the input to be finite.
The length is the total number of bits needed to describe all entries of the
matrix
because we need the number of bits in the input to be finite.
The length is the total number of bits needed to describe all entries of the
matrix
![]() .
.
![]()
So for example if each coordinate has ![]() bits, then the input length is
bits, then the input length is
![]() .
.
A polynomial time algorithm is one that takes at most
![]() input length
input length![]() steps to execute. For example an algorithm
that runs in
steps to execute. For example an algorithm
that runs in
![]() input length
input length![]() steps is a cubic algorithm.
steps is a cubic algorithm.
The shortest vector in a lattice is the zero vector. When we talk about ``the shortest vector'' in a lattice, we mean the shortest non-zero vector.
Finding the shortest vector in a lattice is NP-hard (Ajtai, 2000). Roughly speaking this means that the problem is at least as hard as any combinatorial search problem: if we could solve it in polynomial time, we could use that to solve any other combinatorial search problem in polynomial time. For example we could factor large numbers in polynomial time.
Lovász's lattice reduction algorithm (1980)
which we are about to see is a polynomial time
algorithm, and it does not find the shortest vector in the lattice.
What it does find is a vector in the lattice that is ``short enough.''
Specifically, it finds a vector ![]() with
with
![]() where
where ![]() is the dimension and
is the dimension and
First we need to define a Lovász-reduced basis. Recall the Gram-Schmidt
orthogonalization process for obtaining an
orthogonal basis for the span of a set of
linearly independent vectors. If
![]() is the original basis, and
is the original basis, and
![]() is the orthogonalized basis then we have
is the orthogonalized basis then we have
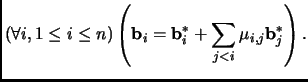
Additionally, we do not want the basis vector
![]() to be too close
to the subspace
to be too close
to the subspace
![]() , the span of
, the span of
![]() ,
i.e., we do not want
,
i.e., we do not want
![]() to have too small norm.
to have too small norm.
The following definition gives a prcise meaning to these two requirements:
Note that the definition is sensitive to order: the same basis vectors in a different order may not form a Lovász-reduced basis.
The following lemma applies to all bases, not only to
L-reduced ones. The lemma will be our key tool to
proving that in a L-reduced basis, the first basis vector is
not much longer than
![]() .
.
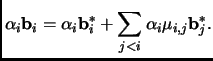
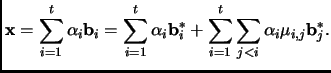
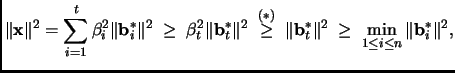
Since
![]() we have
we have
We still have to find a Lovász-reduced basis in ![]() .
.
Lovász's Algorithm
Input:
![]() , non-singular.
, non-singular.
Output:
![]() ,
a Lovász-reduced basis of the same lattice, i.e.,
,
a Lovász-reduced basis of the same lattice, i.e.,
![]() .
.
The algorithm will make two kinds of steps, which try to achieve the
two conditions in the definitions. The first kind will perform
elementary transformations on the basis (replacing
![]() by
by
![]() for a suitable scalar
for a suitable scalar
![]() ) with the goal to make the condition
) with the goal to make the condition
![]() hold. We repeat this type of steps until all
hold. We repeat this type of steps until all ![]() satisfy
this inequality (so condition (1) holds).
satisfy
this inequality (so condition (1) holds).
Once condition (1) has been achieved, we
check for condition (2) and will switch the order of
a pair of consecutive basis vectors where violation is found.
We perform this operation only once per round.
While it is not immediately clear how this kind of rearrangement
is of any help, it is clear that such a rearrangement
may destroy the condition
![]() we have labored hard to achieve, so we must return to
the elementary transformations to restore condition (1).
we have labored hard to achieve, so we must return to
the elementary transformations to restore condition (1).
All in all, it is not evident that such an approach will converge to anything at all; but if it does converge, the result is a Lovász-reduced basis.
Making the
![]() s small
s small
Let
![]() denote
denote
![]() .
If
.
If
![]() are the vectors
produced by the Gram-Schmidt process, then for all
are the vectors
produced by the Gram-Schmidt process, then for all
![]() ,
,
![]() and
and
![]() ; and these two
conditions determine the
; and these two
conditions determine the
![]() . So the
elementary transformations
. So the
elementary transformations
![]()
![]() do not change any of the
do not change any of the
![]() .
.
![]() will produce the same vectors
will produce the same vectors
![]() .
On the other hand, the
.
On the other hand, the ![]() will change; we need to
calculate this change to see that with the appropriate choice
of the coefficient
will change; we need to
calculate this change to see that with the appropriate choice
of the coefficient
![]() , the condition
, the condition
![]() will be achieved.
will be achieved.
Here is then the first procedure:
Procedure ``coefficient reduction''
for ![]() to
to ![]()
for ![]() downto
downto ![]()
![]()
Here
![]() denotes the integer nearest to
denotes the integer nearest to ![]() .
Ties are broken arbitrarily.
.
Ties are broken arbitrarily.
![]()

Complexity analysis: ``coefficient reduction''
requires
![]() elementary
basis transformations, each of which takes
elementary
basis transformations, each of which takes ![]() arithmetic operations.
One more thing to worry about: do the integers involved grow in the
process?
arithmetic operations.
One more thing to worry about: do the integers involved grow in the
process?
Swapping
Now we check property 2. If it is violated, we swap
a violating pair
![]() and
and
![]() . Then we start over with
coefficient reduction again. If property 2 is ever
satisfied after coefficient reduction then we are done.
Here is the full algorithm in pseudocode:
. Then we start over with
coefficient reduction again. If property 2 is ever
satisfied after coefficient reduction then we are done.
Here is the full algorithm in pseudocode:
Procedure ``Lattice Reduction''
while basis not Lovász-reduced
if
![]() then do coefficient reduction
then do coefficient reduction
else find first ![]() such that
such that
![]() ;
;
swap
![]() and
and
![]() ;
;
update orthogonalized sequence.
To prove that this algorithm terminates, we use a potential function argument, a general method of algorithm analysis which assigns a value (the ``potential'') to each ``configuration'' of variables in such a way that each phase of the algorithm reduces the potantial.
The Lovász potential of a basis
![]() is defined to be the quantity
is defined to be the quantity
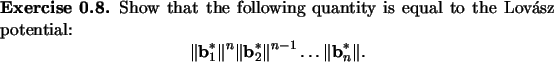
It follows from the exercise that the Lovász potential does not change under the ``coefficient reduction'' procedure. (Why?)


Therefore, for integral lattices,
the Lovász potential is ![]() It follows that
the algorithm terminates in
It follows that
the algorithm terminates in
![]() phases, where
phases, where ![]() is the
initial potential. Since each phase takes
is the
initial potential. Since each phase takes ![]() steps, the algorithm takes
steps, the algorithm takes
![]() steps.
steps.
![]()
