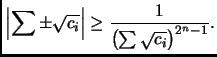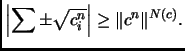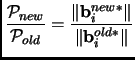Next: About this document ...
Discrete Math, Ninth Problem Set (July 9th)
REU 2003
Instructor: Laszlo Babai
Scribe: David Balduzzi
READING: Please read the handout on irreducibility of polynomials
(last chapter of ``Algebra review'' handout.)
Recall that  is an algebraic number if
is an algebraic number if 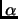 is a root
of some nonzero polynomial
is a root
of some nonzero polynomial 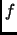 with rational coefficients. If
with rational coefficients. If 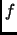 has the lowest possible degree then we call
has the lowest possible degree then we call 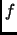 minimal polynomial
of
minimal polynomial
of 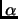 . The degree of
. The degree of 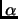 is the degree of its
minimal polynomial.
is the degree of its
minimal polynomial.
Exercise 0.1
Show that the minimal polynomial is irreducible over
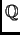
.
Exercise 0.2
Lat
![$ f\in\mathbb{\mathbb C}[x]$](img4.gif)
with
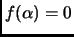
. Then
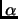
is a multiple root
of
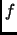
if and only if
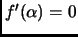
.
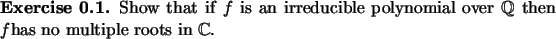
The following straightforward observation is used to great effect in many
arguments about diophantine approximation and algorithm analysis.
Theorem 0.4
Liouville
Let
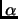
be an algebraic number of degree
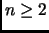
. Then
Sketch of proof:
By assumption we have
![$ f\in{\mathbb{Z}}[x]$](img15.gif) ,
, 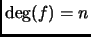 ,
,
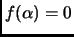 and
and
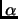 is a simple roort of
is a simple roort of 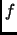 . Therefore
. Therefore 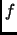 can be
written as
can be
written as
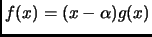 , where
, where
![$ g\in {\mathbb{C}}[x]$](img18.gif) and
and
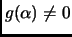 .
Now
.
Now
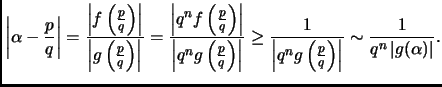 |
(1) |
(Why does
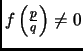 ?) So
?) So
This implies that 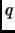 is bounded and therefore
there are only a finite number of solutions.
is bounded and therefore
there are only a finite number of solutions.
Problem 0.5
(
Computational geometry.)
Suppose we are to find the shortest path between two points
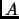
and
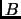
in the plane, avoiding certain straight line segments (``obstacles'').
The obstacles are perpendicular to
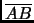
drawn such that they have ``convex boundary.''
Can the number of candidate optimum paths be bounded by 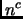 , where
, where
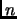 is the number of obstacles? In other words can an algorithm be
found limiting the number of candidate paths to a polynomial number.
is the number of obstacles? In other words can an algorithm be
found limiting the number of candidate paths to a polynomial number.
OPEN PROBLEM 0.6
Given positive integers
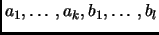
can we decide
in polynomial time (in terms of total bit length) if
Exercise 0.7
Show
where we are taking products over all assignments of signs, with the
restriction that
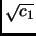
always positive.
Suppose we assume that for no choice of signs does
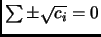 . Then
. Then
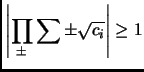
implies
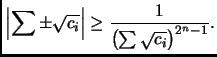
Problem 0.8
Find a sequence
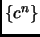
of sequences such that
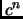
is a collection
of
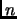
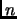
-digit numbers; with the additional property that for some
choice of signs,

log
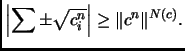
Can

log
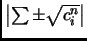
grow faster than
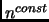
?
Review seventh problem set.
Exercise 0.9
Show coefficient reduction does not affect the sequence
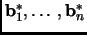
.
Exercise 0.10
We denote the Lovász potential function by
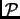
. Show
is a (what?) constant factor. (
Hint: work only in the space
spanned by
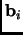
and
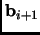
.)



Next: About this document ...
Varsha Dani
2003-07-25
![]() is an algebraic number if
is an algebraic number if ![]() is a root
of some nonzero polynomial
is a root
of some nonzero polynomial ![]() with rational coefficients. If
with rational coefficients. If ![]() has the lowest possible degree then we call
has the lowest possible degree then we call ![]() minimal polynomial
of
minimal polynomial
of ![]() . The degree of
. The degree of ![]() is the degree of its
minimal polynomial.
is the degree of its
minimal polynomial.
![]()
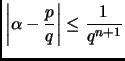
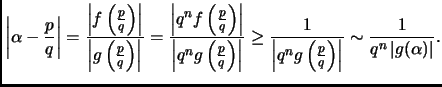
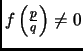 ?) So
?) So
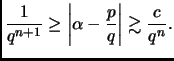
![]() , where
, where
![]() is the number of obstacles? In other words can an algorithm be
found limiting the number of candidate paths to a polynomial number.
is the number of obstacles? In other words can an algorithm be
found limiting the number of candidate paths to a polynomial number.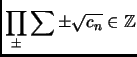
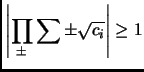 implies
implies