


Next: About this document ...
Up: Graphs
Previous: Automorphisms of finite projective
Definition 3.6
An undirected graph

is
connected if every pair of vertices is
connected by a path. It is
 -connected
-connected if it remains
connected after removing any

vertices (except the complete graph

which is

-connected by convention).
Let

be the maximum

such that

is

-connected.

is called the
vertex-connectivity of

.
Example 3.7
The cycle graph has

for all

. One should think
of this as a topological invariant and all cycles have the same shape.
This requires the convention that

.
Definition 3.8
If

are vertices in a graph

, then the
 -
- -connectivity
-connectivity

is the minimum number of vertices to delete to prevent
there from being a path from

to

. (If there's a direct edge from

to

, count deleting it as deleting a vertex.)
Then

. There is a similar notion

for directed graphs and directed paths from

to

.
There is also the
edge  -
- -connectivity
-connectivity

, the
minimum number of edges to delete to prevent there from being a path
from

to

. This has a global version

and a directed version

.
Theorem 3.9 (Menger)

is also the number of
vertex-disjoint paths from

to

.

is also the number
of edge-disjoint paths from

to

. The analogous directed versions
are also true.



Definition 3.10

is a
vertex-transitive graph if its
automorphism group acts transitively on its vertices. Similarly, it
is
edge-transitive if the automorphism group acts transitively
on the edges. It is
vertex- or
edge-primitive if the
automorphism group acts primitively on the set of vertices (edges,
respectively).





Definition 3.12
A directed graph is
strongly connected if for every pair of
vertices

and

, there is a directed path from

to

. It is
weakly
connected if it is a connected as an undirected graph
when we ignore the orientation of the edges.
Definition 3.13
A directed graph

satisfies the
Euler condition if
for each vertex the in-degree is equal to the out-degree.



A typesetting command error (a signle omitted backslash) rendered
a paragraph unintelligible in the previous handout. It was
the paragraph connecting two theorems. Here we reproduce the two
theorems with the corrected paragraph inbetween.
Theorem 3.15 (B-Seress)
Let

generate

.

.
This result suffers from the ``element-order bottleneck.'' The two tricks
used are commutators and raising elements to powers. A recent result
gives a polynomial upper bound under the condition that one of the generators
fixes 70% of the permutation domain. So now all is left to prove is
that we can reach such a permutation in a polynomially bounded
number of steps. Somebody in this audience may be able to do
this with a fresh idea.
Theorem 3.16 (B-Beals-Seress)
Let

generate

.
If

with the
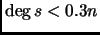
then

(

?). (Recall that the
degree of a permutation is
size of its
support, the set of
elements that it actually moves.)



Next: About this document ...
Up: Graphs
Previous: Automorphisms of finite projective
Varsha Dani
2003-08-04
![]()

![]()
![]()
![]()
![]()
![]()
![]()

![]()
