19.19 DO (counting surjections)   Review the proof from class that the number of $[n]\to [k]$ surjections is $$ \sum_{j=0}^k (-1)^j \binom{k}{j}(k-j)^n $$

19.21 XC (Bonferroni's inequalities) (10 points)   With the notation we used in class (see the slides), the Inclusion-Exclusion formula states that $P(B) = S_0 - S_1 + S_2 +- \dots$.
Prove:
    $P(B) \le S_0$
    $P(B) \ge S_0 - S_1$
    $P(B) \le S_0 - S_1 +S_2$
    $P(B) \ge S_0 - S_1 +S_2 - S_3$
      etc.

19.23 XC (4 points)   Count those $n$-digit integers which have only odd digits, and every odd digit occurs among their digits. (Example for $n=7$:   $5911731$ is counted, $5911531$ is not counted.) Give a simple closed-form expression.

19.25 XC (7 points)   The boss writes $n$ distinct letters to $n$ different correspondents. The secretary puts the letters in the $n$ addressed evelopes in a random order. (a) Let $p_n$ denote the probability that none of the letters go in the right envelope. Compute $p_n$ (give a reasonably simple formula; not a closed-form expression).   (b)   Prove:   $\lim_{n\to\infty} p_n = 1/\eee$ (where $\eee = 2.71\dots$ is the base of the natural logarithm).

18.15 STUDY   PROB 7.8, especially 7.8.14 (Markov's Inequality), PROB 7.9 (variance, standard deviation, covariance, Chebyshev's Inequality), PROB 7.10--7.11 (independence of random variables)

18.19 DO   If $X,Y$ are independent random variables then $E(XY)=E(X)E(Y)$.

18.21 DO   Prove: If $X$ is almost constant (takes the same value with probability 1) and $Y$ is any random variable then $X$ and $Y$ are independent.

18.23 DO   Prove: If $X$ and $Y$ are independent, not almost constant random variables then $|\Omega|\ge 4$.

18.25 DO   (a)   If $X,Y$ are independent and $c\in \rrr$ then $X+c$ and $Y$ are independent.   (b)   If $X,Y$ are uncorrelated and $c\in \rrr$ then $X+c$ and $Y$ are uncorrelated.

18.27 DO   Prove: if $|\Omega|=2$ and $X,Y$ are uncorrelated then $X$ or $Y$ is almost constant (and therefore $X$ and $Y$ are independent).

18.29 DO   Consider the uniform probability space with $|\Omega|=3$. Find two random variables, $X,Y$ such that the ranges of $X$ and $Y$ are subsets of $\{-1,0,1\}$, and $X$ and $Y$ are uncorrelated but not independent.

18.35 HW (6 points)   Consider a poker hand. Let $X$ denote the number of Aces and $Y$ the number of Spades in the poker hand. Prove that these random variables are not independent.

18.39 XC (10 points)   Let $r,s \ge 2$ and $0\le k\le rs$. Consider a generalized standard deck of cards with $rs$ cards in the deck where there are $r$ cards of each kind (like $r$ Aces) and $s$ cards in each suit (like $s$ spades). Let a generalized poker hand consist of $k$ cards. Consider a poker hand. Let $X$ denote the number of Aces and $Y$ the number of Spades in the poker hand. Prove that these random variables are uncorrelated.

18.45 DO (variance of sum)   PROB 7.9.17

18.47 DO (additivity of variance)   PROB 7.9.18

18.60 RANDOM GRAPHS -- The Erdős--Rényi model

This burgeoning field was created in a single paper by Paul Erdős and Alfréd Rényi in 1960.

18.61 DEF   The $\bfG(n,p)$ model where $n$ is a positive integer and $0 < p < 1.$
We fix a set $V$ of $n$ vertices. For each pair $\{u,v\}$ of distinct vertices we flip a biased coin to decide whether to join $u$ and $v$ by an edge; we join them if the coin comes up Heads. The probability of this event is $p$, and these $\binom{n}{2}$ events are independent.
In Exercise 18.65 we give an exact definition of the probability space and show that this wish-list is indeed satisfied.

18.63 DEF (continued)   In this model, the sample space $\Omega$ is the set of all graphs on vertex set $V$, so $|\Omega|=2^{\binom{n}{2}}$, and for the graph $G\in\Omega$ we have $$ P(G) = p^m(1-p)^{\binom{n}{2}-m}$$

18.65 DO   Verify that   (a)   the function $P$ defined in the preceding exercise is indeed a probability distribution on $\Omega$ and   (b)   for every pair $\{u,v\}$ of distinct vertices, the even $i\sim j$ indeed has probability $p$, and   (c)   these $\binom{n}{2}$ events are indeed independent, as desired.

18.67 Convention   We denote our random graph (an element picked from our sample space according to the $\bfG(n,p)$ distribution) by $\calG$. So the elementary event $G\in\Omega$ can also be written as the event "$\calG=G$".

18.69 DO   Prove:   (a)   The expected number of edges of $\calG$ is $p\binom{n}{2}$   (b)   The expected number of triangles in $\calG$ is $p^3\binom{n}{3}$.

18.71 DO   Let $3\le k\le n$. Compute the expected number of $k$-cycles in $\calG$. Your answer should be a very simple closed-form expression in terms of $n,p$, and $k$.

18.73 DO   Prove: The variance of the number of edges of $\calG$ is $p(1-p)\binom{n}{2}$.

18.75 HW (10+7+7 points)   Let $X_n$ denote the number of triangles in the random graph $\calG$ in the $\bfG(n,p)$ model.   (a)   Calculate $\var(X_n)$. Give a reasonably simple closed-form expression.   (b)   The answer will be a polynomial in $n$. What is the degree of this polynomial?   (c)   Asymptotically evaluate $\var(X_n)$ as $p$ is fixed $(0 < p < 1)$ and $n\to\infty$. Your answer should be of the form $\var(X_n)\sim a(p)n^b$ where $b$ is a constant and $a$ is a function of $p$. Determine $a$ and $b$.
Hint.   PROB 7.9.17 (variance of sum)

17.15 REVIEW   PROB Section 7.2

17.18 STUDY   PROB 7.3 (conditional probability, Theorem of Complete Probability, Probability of causes), PROB 7.4 (independence of a pair of events, positive/negative correlation, PROB 7.5 (independence of multiple events), PROB 7.8 (random variables, expected value, indicator variables)

17.21 DO   PROB 7.3.2

17.25 STUDY (Bayes's equation: probability of causes)   PROB 7.3.3

17.27 DO   PROB 7.3.4

17.29 HW (1+3+4+3 points)   PROB 7.3.5

17.31 STUDY (Theorem of Complete Probability)   PROB 7.3.7

17.33 HW (4+5+3 points)   PROB 7.3.8   (probability of causes)

17.37 HW (3 points)   PROB 7.4.4   (independence of complement)

17.39 DO   PROB 7.4.5   (independence of trivial event)

17.41 HW (2 points)   PROB 7.4.6   (odd vs square on die)

17.43 HW (4 points)   PROB 7.4.8   (uniform space of prime size)

17.45 HW (4 points)   PROB 7.4.9   (2 indep nontriv events $\Rightarrow$ $|\Omega|\ge 4$)

17.47 XC (7 points)   PROB 7.4.12   (correlation of $2\mid x$ and $3\mid x$)

17.49 HW (3 points)   PROB 7.4.13   (give a very short proof)

17.51 HW (4 points)  PROB 7.4.14   (union vs intersection)

17.53 DO   PROB 7.4.15   ($A$ vs $A$)

17.57 DO   PROB 7.5.3   (indepenence of complement for 3 events)

17.59 DO   PROB 7.5.4   (indepenence of trivial event for 3 events)

17.61 HW (4 points)   PROB 7.5.5(b)   (independence of union)

17.63 XC (4 points)   PROB 7.5.6   ($|\Omega|\ge 8$)

17.65 HW (5+5 points)   PROB 7.5.7.   Conceptual clarity is paramount.

17.67 DO   PROB 7.5.9(a)   (3 events, intersection ok, but not pairwise independent)

17.69 XC (5 points)   PROB 7.5.9(b)   (same with balanced events)

17.71 STUDY   the rest of Section 7.5 (independence of multiple radom variables)

17.75 DO   PROB 7.5.17, 7.5.18 (independence of complements)

17.77 XC (5 points)   7.5.19

17.79 XC (6 points)   PROB 7.5.20   ($(n-1)$-wise indep events). Simplicity is paramount.

17.99 DO   PROB 7.8.3   (alternative definition of expected value)

17.101 HW (3 points)   PROB 7.8.5   (expected value is between the minimum and the maximum). Here $\min X = \min_{a\in\Omega} X(a)$. $\max X$ is defined analogously.

17.103 DO   PROB 7.8.6   (additivity of expectation)

17.105 DO   PROB 7.8.7   (linearity of expectation)

17.107 DEF   PROB 7.8.8   (indicator variable), PROB 7.8.9 (indicator $\vt_A$ indicating event $A$)

17.109 DO   PROB 7.8.10   (bijection between events and indicator variables)

17.111 DO   PROB 7.8.11   ($E(\vt_A) = P(A)$)

In the following sequence of exercises, use indicator variables. About half the score goes for the rigorous definitions of those variables.

17.113 HW (6 points)   PROB 7.8.15   (expected number of Aces, spades in poker hand)

17.115 HW (7 points)   PROB 7.8.16   (expected number of runs of $k$ heads; coin biased)

17.117 HW (6 points)   PROB 7.8.21   (mismatched letters)

17.119 HW (8 points)   PROB 7.8.18   (Club of 2000)

17.121 XC (7 points)   PROB 7.8.20   (number of distinct prime divisors) (use a result from PROB 7.7)

17.XX   PROB 7.8

17.XX   PROB 7.8

More to follow. Please check back later.

As before, in the next sequence of definitions and exercises, $G=(V,E)$ is a graph with $n\ge 1$ vertices.

16.20 STUDY   DMmini Terminology 6.1.42, first two items: clique, clique number, independent set, independence number.
Notation:   $\omega(G)$ denotes the clique number of the graph $G$ (cardinality of the largest clique) and $\alpha(G)$ denotes the independence number of $G$ (cardinality of the largest independent set). So $\alpha(G) = \omega(\Gbar)$.

16.23 DO   Every subst of an independent set is an independent set. In particular, the empty set is an independent set.

16.25 DO   $1 \le \alpha(G) \le n$.

16.27 HW (3+3 points)   (a)   $\alpha(G) = 1$ if and only if $G\cong K_n$.   (b)   $\alpha(G) = n$ if and only if $G \cong \Kbar_n$.

16.29 HW (4+4+1 points)   (a)   Find a connected graph $G$ of order $n$ such that $\alpha(G)=n-1$.   (b)   Prove that this graph is unique (up to isomorphism), i.e, if $G$ and $H$ are two connected graphs of order $n$ with $\alpha(G)=\alpha(H)=n-1$ then $G\cong H$.   (c)   We have a standard notation for this graph; what is it?

16.31 REVIEW   the greedy coloring algorithm, described in pseudocode in the handout GreedyCol (click Texts > GreedyCol).

16.33 DEF (maximal vs. maximum)   An independent set $A\subseteq V$ is a maximum independent set if $|A|=\alpha(G)$, i.e., $A$ has the maximum possible cardinality. We say that $A$ is a maximal independent set if $A$ is not a proper subset of any independent set, i.e., if $A\subseteq B\subseteq V$ and $B$ is an independent set then $B=A$.

16.35 HW (5 points)   (a)   Describe the greedy independent set algorithm in pseudocode, modeled after the greedy coloring algorithm. The pseudocode should be very simple. It can use English phrases, but the definition of its variables and its cycle structure should be rigorous.   (b)   Prove that your algorithm finds a maximal independent set.

16.37 DO   Review from class the proofs that   (a)   $\alpha(P_n) = \lceil n/2\rceil$   and   (b)   $\alpha(C_n) = \lfloor n/2\rfloor$. (See the slides.)
Recall that the proofs of the upper bounds, $\alpha(P_n) \le \lceil n/2\rceil$   and   $\alpha(C_n) \le \lfloor n/2\rfloor$, amount to finding independent sets of the stated cardinalities, and in each case, this is achieved by the greedy independent set algorithm.
The elusive part is the proof of the lower bounds. Here we are up against all independent sets, we need to prove the upper bound for all of them. So the proof begins by saying "Let $A$ be an independent set." We have no control over this set, we are not constructing it, it is brought to us by an adversary who intends to prove us wrong. We need to prove our upper bound on $|A|$ for this unknown set $A$.
For (a) we used the Pigeon Hole Principle. For (b), we used a linear relaxation: a set of linear inequalities satisfied by the coordinates of the characteristic vector of $A$, which is the $(0,1)$-vector indicating membership in $A$: it is the vector $(x_i \mid i\in V)$ where $x_i=1$ if $i\in A$ and $x_i=0$ if $i\notin A$.

16.39 HW (5 points)   Let $G$ be a regular graph. Assume $E\neq \emptyset$. Prove:   $\alpha(G) \le \lfloor n/2 \rfloor$.

16.41 HW (5+4+4 points)   (a)   $\alpha(G)\cdot\chi(G) \ge n$.   (b)   Show that this lower bound is tight in the following sense. For every $k,\ell \ge 1$, there exists a graph $G(k,\ell)$ with $n=k\ell$ vertices such that $\alpha(G(k,\ell))=k$ and $\chi(G(k,\ell))=\ell$.   (c)   Show that the lower bound in (a) is far from tight in the following sense. For every $n$, find a graph $G_n$ with $n$ vertices such $\alpha(G_n)\cdot\chi(G_n) = \Omega(n^2)$. State the constant hidden in the big-Omega notation. Make it as large as you can.

16.43 XC (9 points)   For $k,\ell \ge 3$, let $T(k,\ell)=C_k\Box C_{\ell}$ denote the $k\times \ell$ toroidal grid. Assume $k,\ell$ are odd. Determine $\alpha(T(k,\ell))$. Your result should be a simple closed-form expression of $k$ and $\ell$.

16.45 Notation (smallest maximal independent set)   We shall denote the cardinality of the smallest maximal independent set of $G$ by $\beta(G)$. (This is not standard notation, only for this class.)

16.46 DO   Observe that $\beta(G) \le \alpha(G)$.

16.47 DO   Verify:   $\beta(P_5)=2$ (while $\alpha(P_5)=3$).

16.49 HW (8 points)   Determine $\beta(C_n)$ for all $n\ge 3$.

16.51 HW (7+4 points)   (a)   For $n\ge 3$, determine the number of maximum independent sets of $C_n$.   (b) True or false: this number is   (b1)   $O(n)$   (b2)   $\Theta(n)$ .

16.53 XC (5 points)   Determine the number of independent sets in $P_n$. Express your answer in terms of a familiar function of $n$.

16.55 XC (7 points)   Prove that the number of maximal independent sets in $P_n$ grows simply expnentially as a function of $n$.
You need to give both a simply exponential upper bound and a simply exponential lower bound on this quantity.

16.XX  

16.64 STUDY   PROB Section 7.2.

16.65 HW (5 points)   PROB 7.2.4 (a). You need to review Notation PROB 7.1.2 and PROB 7.2.3, part 1.

16.67 HW (4 points)   PROB 7.2.8 (counting trivial events).

16.69 DO   Prove the Modular equation (PROB 7.2.14).

16.71 HW (6 points)   Prove the Union bound (PROB 7.2.16). Proceed by induction on $k$.

16.73 DEF   We say that the event $A$ is balanced if $P(B)=1/2$.

16.75 DO (Inclusion-Exclusion for 3 events)   Let $A,B,C\subseteq\Omega$ be three events. Prove: $$ P(A\cup B\cup C) = P(A)+P(B)+P(C)-P(A\cap B)-P(A\cap C)-P(B\cap C) + P(A\cap B\cap C)$$

16.77 XC (8 points)   Find the smallest value of the real number $p$ such that there exists a finite probability space $(\Omega,P)$ and three balanced events $A,B,C\subset\Omega$ such that $P(A\cap B)=P(A\cap C) = P(B\cap C)=p$. State the smallest possible size of the sample space for the minimum value of $p$.

16.XX  

16.XX  

16.XX  

More to follow. Please check back later.

15.10 STUDY   DMmini Chap 2 (Asymptotic notation) Section 2.3 (Little-oh and little-omega notation), Section 2.4 (Big-Oh, Big-Omega, Big-Theta notation), Section 2.7 (Problems).

15.13 DEF (little-oh notation)   DMmini 2.3.1 (definition of the $a_n = o(b_n)$ relation: "$a_n$ is little-oh $b_n$"

In the exercises below, $(a_n), (b_n), (c_n)$ are sequences of real (or complex) numbers.

15.15 HW (4 points)   Given the sequence $(b_n)$, there exists a sequence $(a_n)$ such that $a_n = o(b_n)$ if and only if $b_n$ is eventually nonzero.

15.17 DO   $a_n \sim b_n \Leftrightarrow a_n-b_n = o(b_n) \Leftrightarrow a_n-b_n = o(a_n)$

15.21 DO   DMmini 2.3.2   ($a_n=o(c_n) \wedge b_n=o(c_n) \Rightarrow a_n\pm b_n = o(c_n)$)

15.23 DO   $a_n = o(b_n) \Rightarrow (\forall c\in\rrr)(c\cdot a_n = o(b_n))$

15.25 HW (4 points)   Find sequences $(a_n)$, $(b_n)$, $(c_n)$ such that $a_n = o(b_n)$ and $a_n = o(c_n)$ and $(\forall n)(b_n+c_n\neq 0)$ but $a_n$ is not $o(b_n+c_n)$.

15.27 HW (4 points)   DMmini 2.36   (find $a_n, b_n > 1$ such that $a_n = o(b_n)$ but $\ln a_n \sim \ln b_n$)

15.29 DO   If $a_n = o(b_n)$ then eventually $|a_n| < |b_n|/100$.

15.31 DO   (a)   $a_n = o(b_n) \Leftrightarrow a_n^2 = o(b_n^2)$
  (b)   Let $a_n, b_n > 0$. Then $a_n = o(b_n) \Leftrightarrow \sqrt{a_n} = o(\sqrt{b_n})$

15.33 XC, due Nov 28 (5+5 points)   DMmini 2.3.7 (comparing the relations $a_n = o(b_n)$ and $\ln a_n = o(\ln b_n)$ where $a_n,b_n > 1$)

15.35 DO   Let $f,g$ be polynomials. Then $f(n) = o(g(n))$ if and only if $\deg(f) < \deg(g)$.
Example:   $25n^2+200n+1000 = o(n^3 - 15n^2-10^6)$

15.41 Theorem (L'Hôpital's rule)   $L\in \Rbbar$ and let $f$ and $g$ be real functions defined and differentiable in a neighborhood of $L$ except possibly at $L$. Assume $\lim_{x\to L} f(x)=\lim_{x\to L} g(x) = M$ where $M = 0$ or $\infty$. If the limit $\displaystyle{\lim_{x\to L}\frac{f'(x)}{g'(x)}}$ exists, then $\displaystyle{\lim_{x\to L}\frac{f(x)}{g(x)}}$ also exists, and $$ \lim_{x\to L} \frac{f(x)}{g(x)} = \lim_{x\to L} \frac{f'(x)}{g'(x)} $$

15.43 DO   $\displaystyle{\lim_{x\to\infty} \frac{\ln x}{x} = 0}$.    Apply L'Hôpital's rule.

15.45 DO   For every $c > 0$,   $\displaystyle{\lim_{x\to\infty} \frac{\ln x}{x^c} = 0}$.

Give two proofs.   (a)   Apply L'Hôpital's rule.   (b)   Do not use L'Hôpital's rule. Use bootstrapping instead: use the preceding exercise, substituting $y=x^c$ as a new variable.

15.47 HW (3 points)   Prove:   $(\ln n)^{100} = o(n)$.

15.51 DO (exponential growth beats polynomial growth 1)   Prove:   $n^{100} = o(1.001^n)$.

15.53 DO   $n^{50} = o(1.001^{\sqrt{n}})$.
Bootstrapping: use the preceding exercise with an appropriate new variable.

15.55 DO (exponential growth beats polynomial growth 2)   Let $c, C, \epsilon > 0$. Prove:   $n^C = o((1+c)^{n^{\epsilon}})$.

15.71 DEF (little-omega notation)   DMmini 2.3.8

15.73 HW (3 points)   $n! = \omega\left((n/\eee)^n\right)$

15.77 DO   $a_n =\omega(b_n) \wedge a_n = \omega(c_n) \Rightarrow a_n = \omega(b_n + c_n)$

15.79 DO   (a)   $a_n = \omega(c_n) \wedge b_n =\omega(c_n) \not\Rightarrow a_n+b_n =\omega(c_n)$.
  (b)   If $a_n b_n > 0$ then   $a_n = \omega(c_n) \wedge b_n =\omega(c_n) \Rightarrow a_n+b_n =\omega(c_n)$.

15.81 XC, due Nov 28 (5 points)   Let $a_n > 0$. Prove: if $a_{n+1} = \omega(a_n)$ then $\ln a_n =\omega(n)$.

15.XX  

15.91 DEF (big-Oh notation)   We say that $a_n = O(b_n)$ ("$a_n$ is big-Oh of $b_n$") if there exists $C\in\rrr$ such that for all sufficiently large $n$ we have $|a_n| \le C\cdot |b_n|$.

15.93 DEF (big-Omega notation)   We say that $a_n = \Omega(b_n)$ ("$a_n$ is big-Omega of $b_n$") if $b_n = O(a_n)$.

15.95 DO   Prove:   $a_n = \Omega(b_n)$ if and only if there exists $c > 0$ such that for all sufficiently large $n$ we have $|a_n| \ge c\cdot |b_n|$.

15.97 DEF (big-Theta notation)   We say that $a_n = \Theta(b_n)$ ("$a_n$ is big-Theta of $b_n$") if $a_n = O(b_n)$ and $a_n = \Omega(b_n)$. If this is the case, we say that $(a_n)$ and $(b_n)$ have the same rate of growth.

15.99 DO   Prove:   $a_n = \Theta(b_n)$ if and only if there exist $c,C > 0$ such that for all sufficiently large $n$ we have $c|b_n| \le |a_n|\le C|b_n|$.

15.105 HW (5 points)   Observe that $\Theta$ is a relation on the set of all sequences. Prove: $\Theta$ is an equivalence relation.

15.107 DO   Prove: if $a_n\sim b_n$ then $a_n = \Theta(b_n)$.

15.111 DO   Assume $a_n/b_n$ has a limit:   $\lim_{n\to\infty} a_n/b_n = L$ (where $L\in \Rbbar$). Prove:
  (a)   If $L=0$ then $a_n = o(b_n)$.
  (b)   If $L=\pm\infty$ then $a_n =\omega(b_n)$.
  (c)   If $L \in\rrr$ and $L\neq 0$ then $a_n = \Theta(b_n)$.

15.113 HW (3 points)   Find sequences $a_n, b_n > 0$ such that $a_n = \Theta(b_n)$ but the limit $\lim_{n\to\infty} a_n/b_n$ does not exist.

15.115 XC, due Nov 28 (5+5points)   DMmini 2.4.7 (comparing the relations $a_n=\Theta(b_n)$ and $\ln a_n \sim \ln b_n$).

15.119 TERMINOLOGY   We say that the sequence $(a_n)$ grows quadratically if $a_n = \Theta(n^2)$. We say that $(a_n)$ grows at most quadratically if $a_n = O(n^2)$. We say that $(a_n)$ grows at least quadratically if $a_n = O(n^2)$.

15.121 TERMINOLOGY   We say that the sequence $a_n$ is polynomially bounded if there exists $C\in\rrr$ such that $a_n = O(n^C)$. Note that this is an upper bound.

15.123 XC, due Nov 28 (5 points)   Let $a_n \ge 1$. Prove: $a_n$ is polynomially bounded if and only if $\ln a_n = O(\ln n)$.

15.125 TERMINOLOGY   We say that the sequence $a_n > 0$ grows exponentially if there exist $c,\epsilon > 0$ such that $a_n = \Omega((1+c)^{n^{\epsilon}})$. Note that this is a lower bound.

15.127 DO (exponential growth beats polynomial growth 3)   Let $a_n, b_n > 0$. Assume $a_n$ is polynomially bounded and $b_n$ grows exponentially.   Prove: $a_n = o(b_n)$.

15.129 XC, due Nov 28 (intermediate growth) (5 points)   Find a sequence $a_n > 0$ such that no subsequence of $(a_n)$ is polynomially bounded and no subsequence of $(a_n)$ grows exponentially.

15.133 TERMINOLOGY   Let $a_n > 1$. We say that the sequence $(a_n)$ grows simply exponentially if $a_n = \eee^{\Theta(n)}$, meaning that $\ln a_n = \Theta(n)$. We say that $a_n$ grows at most simply exponentially if $a_n = \eee^{O(n)}$ and at least simply exponentially if $a_n = \eee^{\Omega(n)}$. We say that $a_n$ grows less than ("slower than") simply exponentially if $a_n = \eee^{o(n)}$ and more than ("faster than") simply exponentially if $a_n = \eee^{\omega(n)}$.

15.135 DO   (a)   $n!$ grows faster than simply exponentially.   (b)   $(\lceil n^{0.9}\rceil )!$ grows slower than simply exponentially.

15.137 XC, due Nov 28 (5+5 points)   Let $a_n > 1$.   (a)   If $a_{n+1} \sim a_n$ then $(a_n)$ grows slower than simply exponentially.   (b)   Find a sequence $(a_n)$ such that $a_{n+1}\sim a_n$ but $a_n$ grows exponentially.

15.139 DO Let $a_n > 1$.   (a)   If $a_{n+1}= O(a_n)$ then $(a_n)$ grows at most simply exponentially.   (b)   Find a sequence $(a_n)$ that satisfies $a_{n+1}= \Omega(a_n)$ but $a_n = o(1)$.

15.151 XC, due Nov 28 (8 points)   Let $G$ be a triangle-free graph. Prove:   $\chi(G) = O(\sqrt{n})$. State the hidden constant you get; make it as small as you can. (We are talking about the constant hidden in the big-Oh notation.)

15.153 XC, due Nov 28 (6 points)   Let $g_n$ denote the number of non-isomorphic graphs of order $n$. (See 10.41.) Prove:   $\log_2 g_n \sim n^2/2$.

15.155 HW, due Nov 28 (4 points)   Let $G$ be a triangle-free graph of order $n$. Let $u,v$ be adjacent vertices of $G$. Prove:   $\deg(u)+\deg(v) \le n$.

15.157 XC, due Nov 28 (6 points)   Let $G$ be a triangle-free graph of order $n$. Prove:   $m\le n^2/4$ (where $m$ is the size of $G$, i.e., the number of edges).
Proceed by induction on $n$ in steps of 2: remove a pair of adjacent vertices.

15.159 XC, due Nov 28 (10 points)   Let $G$ be a 4-cycle-free graph ($G$ has no subgraph isomorphic to $C_4$). Prove:   $m=O(n^{3/2})$.

15.XX  

15.XX  

14.21 HW (Fermat's little Theorem) (6 points)   Let $p$ be a prime number and $a\in\zzz$. Then $a^p\equiv a \pmod p$.
For $a\ge 0$ proceed by induction on $a$. Use a previous exercise. Then reduce the case of negative $a$ to the case of positive $a$.

Remark.   This elementary result should not be confused with Fermat's Last Theorem, a problem that was open for three and a half centuries, until Andrew Wiles proved it in 1995.
The drama around Wiles's proof, which initially contained a gap, became the subject of a musical, Fermat's Last Tango, that features, among others, characters from the Aftermath: Pythagoras, Euclid, Newton, and Gauss, who, in the end, decide to admit Wiles's character to the Aftermath.

14.23 HW (5 points)   Let $p$ be a prime number, $a\in\zzz$, and let $k,\ell$ be positive integers such that $k\equiv\ell \pmod{p-1}$. Prove:   $a^k \equiv a^{\ell} \pmod p$.

Remark.  This result, an immediate consequence of Fermat's little Theorem (FlT), is at the heart of the RSA cryptosystem which is the basis of e-commerce, a trillion-dollar industry.

14.27 DO   Study Petersen's graph (DMmini Section 6.2, page 53, Figure 6.8). Show that the graphs shown in DMmini, Figures 6.8 and 6.9 are isomorphic.
This is the most famous of all graphs; it has a host of remarkable properties. In its unique beauty and symmetry it ranks close to the dodecahedron which is a "double cover" of Petersen's graph. Petersen's graph appears on the cover of the Journal of Graph Theory.

14.29 HW (4 points)   Prove: the chromatic number of Petersen's graph is 3.

14.35 STUDY   the handout GreedyCol (The greedy coloring algorithm). (Click "Texts" on the banner.)

14.37 DO   GreedyCol Problem (a) ("greedy coloring is not so bad")

14.39 HW (6 points)   GreedyCol Problem (b) ("greedy coloring is terrible")

14.45 DEF   Let $r\ge 2s$ where $r,s$ are positive integers. Kneser's graph $\Kn(r,s)$ has $\binom{r}{s}$ vertices labeled with the $s$-subsets of $[r]$: $$V(\Kn(r,s)) = \left\{v_A \mid A\in \binom{[r]}{s}\right\}\,$$ Two vertices, $v_A$ and $v_B$, are adjacent if $A\cap B=\emptyset$.

14.47 HW (4 points)   Prove that $\Kn(5,2)$ is isomorphic to Petersen's graph. Draw a picture of Petersen's graph and label the vertices by unordered pairs from the set $[5]$ so that adjacency corresponds to disjointness.

14.49 HW (4 points)   Prove that $\Kn(r,s)$ is a regular graph. What is its degree? Give a simple closed-form expression.

14.53 XC (7 points)   Prove:   $\chi(\Kn(r,s))\le r-2s+2$.
Remark.   This is actually the exact chromatic number, but the lower bound is much more difficult to prove; for two decades, it was an open problem ("Kneser's Conjecture", 1956), until László Lovász proved it in 1978 by reducing the problem to a result in analysis (the Bosuk-Ulam Theorem, see Wikipedia) using basic concepts of algebraic topology (homotopies). Within weeks of Lovász's proof, Imre Bárány found another, much simpler reduction of Kneser's conjecture to the Borsuk-Ulam Theorem, using a lemma by David Gale from convex geometry.

14.59 STUDY   DMmini, Section 6.2 (Planarity), up to and including Exercise 6.2.10.

14.61 DO   Prove that every tree is planar.

14.65 HW (6 points)   Prove that every planar graph is 6-colorable. Proceed by induction on the number of vertices. Use only the following facts about planar graphs:
  (a)   every subgraph of a planar graph is planar
  (b)   every planar graph has a vertex of degree $\le 5$ (assuming it has at least one vertex).

14.XX  

14.XX  

14.80 STUDY   ASY, Chapters 5-6.

Below, $(a_n)$ and $(b_n)$ will denote sequences of real numbers. We permit that a finite number of members of these sequences may be undefined.

14.81 DEF   We say that $(a_n)$ is asymptotically equal to $(b_n)$ (denoted $a_n \sim b_n$) if $\lim_{n\to\infty} a_n/b_n = 1$.

14.83 DO   ASY 5.5 (a) and (b)   (asymptotics of polynomials)

14.85 HW (5 points)   Prove:   if $a_n \sim b_n$ then both $a_n$ and $b_n$ are eventually nonzero.

14.87 HW (4+1 points)   ASY 5.5 (c) and (d)   (asymptotics of a quotient of polynomials)

14.89 HW (4 points)   ASY 5.5 (e)   (asymptotics of $\binom{n}{5}$)

14.93 DEF   ASY 5.6   (polynomials: coefficients, degree)

14.95 DO   ASY 5.7   (degree of sum and product of polynomials)

14.96 DO   Let $f(x)$ be a polynomial of degree $k\ge 0$ with leading term $a_kx^k$. Prove: $f(n)\sim a_kn^k$. (A polynomial is asymptotically equal to its leading term.)

14.97 HW (4 points)   ASY 5.8 (a)   (asymptotics of quotients of polynomials). Make your proof very simple based on previous exercises. Simplicity counts.

14.99 XC (4+4 points)   ASY 5.8 (b) and (c) (asymptotics of $\sin(1/n)$ and $\ln(1+1/n)$)

14.101 HW (5 points)   ASY 5.8 (d)   (asymptotics of $\sqrt{n^2+1}-n$)

14.103 DO   ASY 5.9   (asymp. equality vs derivative)

14.105 HW (4 points)   ASY 5.10   ($a_n\sim b_n \not\Rightarrow a_n^n \sim b_n^n$)

14.107 STUDY   ASY 5.11   (Stirling's formula)

14.109 HW (4 points)   ASY 5.12   (asymptotics of middle binomial coefficient)

14.111 DEF   ASY 5.13   (prime counting function $\pi(x)$)

14.113 STUDY   ASY 5.14   (Prime Number Theorem)

14.115 DO   ASY 5.15   (chance of a random integer being prime). This exercise is needed to make the RSA cryptosystem efficient.

14.117 DO   ASY 6.2   (convergence vs asymptotic equality)

14.119 HW (5 points)   ASY 6.3   ($\sim$ is an equivalence relation on the set of eventually nonzero sequences). In each part, state what property of limits you are using and give the relevant exercise number from ASY, Chapter 3.

14.121 HW (5 points)   Let $a_n, b_n > 1$. Assume $a_n\sim b_n$. Show that the relation $a_n-1 \sim b_n-1$ does NOT follow from this assumption.

14.123 DO   Observe that the preceding exercise solves ASY 6.4 (a)   (cannot add asymptotic equalities)

14.125 XC (4 points)   ASY 6.4 (b)   (we can add asymptotic equalities of sequences of numbers of the same sign)

14.127 DEF   ASY 6.6   (being bounded away from a number)

14.129 HW (4 points)   Let $a_n, b_n > 1$. Assume $a_n \sim b_n$. Prove: if $a_n$ is bounded away from $1$ then $b_n$ is also bounded away from $1.$

14.131 HW (4 points)   ASY 6.5 (a)   (cannot take logarithm)

14.133 XC (4 points)   ASY 6.5 (b)   (can take logarithm)

14.135 XC (5 points)   ASY 6.7   (squeeze principle)   Note that you need to show that $b_n$ is eventually nonzero.

14.137 DO   ASY 6.8 (a)   (lower bound on $n!$)   (recall: this was Exercise 3.38)

14.139 HW (3+4 points)   ASY 6.8 (b) and (c)   (previous exercise vs Stirling's formula)

14.141 XC (3+4 points)   ASY 6.9 (a) and (b)   ($\ln(n!) \sim n\ln n$)

14.143 XC, due Nov 28 (6 points)   ASY 6.10   (asymptotics of $n$-th prime number)

13.11 STUDY (really)   the handout "Asymptotic Equality and Inequality" (ASY), Section 1 (Sequences) and Section 3 (Limits).

13.15 DO   State in plain English what it means that a sequence is NOT eventually nonzero. (Discussed in class. See the answer at the end of the Class 12 material: 12.100.)

13.17 HW (3+4 points)   (a)   Define what it should mean for a sequence $(a_n)$ to be eventually increasing. Your answer should be a simple quantified formula.   (b)   Find a sequence $(b_n)$ such that $b_n\to\infty$ but the sequence is not eventually increasing.

13.19 NOTATION   $\rrr$ denotes the set of real numbers. $\pm\infty$ are not numbers, but they can be limits of sequences; we write $\Rbbar$ to denote the set $\rrr\cup\{\infty,-\infty\}$.

13.21 TERMINOLOGY   We say that the sequence $(a_n)$ has a limit if $(\exists L\in\Rbbar)(a_n \to L)$. We say that $(a_n)$ converges (or $(a_n)$ is a convergent sequence) if $(\exists L\in\rrr)(a_n \to L)$. In other words, the sequence $(a_n)$ is convergent of it has a finite limit. A sequence that is not convergent is divergent. So if a divergent sequence has a limit at all, the limit must be $\pm\infty$.

13.25 DO (limit of subsequence)   Let $J\subseteq I\subseteq \nnn_0$ be infinite subsets of $\nnn_0$. Let $L\in \Rbbar$. Prove: if $\lim_{n\in I} a_n = L$ then $\lim_{n\in J} a_n = L$.

13.27 HW (5 points)   Prove that a sequence can have at most one limit. In other words, if $L,M\in\Rbbar$ and $a_n\to L$ and $a_n\to M$ then $L=M$.

13.29 XC (6 points)   Find a sequence $S$ such that every real number is the limit of some subsequence of $S$.

13.31 DEF (bounded sequence)   ASY Def 3.12.

13.33 HW (5+2 points)   (a)   Prove: every convergent sequence is bounded.   (b)   Find a bounded sequence that is divergent. Prove the divergence of your sequence using 13.25 and 13.27.

13.35 HW (4 points)   Prove: if $a_n\to -\infty$ then $a_n$ is bounded from above.

13.39 DEF   The finite limit of a sequence of of complex numbers is defined by the exact same formula as for real numbers. A sequence of complex numbers is convergent if it has a finite limit and divergent otherwise.

13.41 HW (4+4 points)   Let $z\in\ccc$. Consider the sequence of powers of $z$:  $(z^n\mid n\in\nnn_0)$.   (a)   Prove: if $|z| > 1$ then this sequence is divergent.   (b)   Prove: if $|z| < 1$ then this sequence is convergent.  

13.43 XC (6 points)   Find all complex numbers $z$ of absolute value $|z|=1$ such that the sequence of powers of $z$ is convergent.

13.47 DO (Bolzano--Weierstrass theorem)   Every bounded sequence of real (or complex) numbers has a covergent subsequence.

13.51 DO   ASY 3.15--3.20. (DO, really.) This sequence of exercises includes the limits of sums, products, quotients.

13.53 XC (5 points)   Find an infinite matrix $(a_{ij} | i,j\in \nnn_0)$ of real numbers such that every row $R_i=(a_{ij}\mid j\in \nnn_0)$ tends to zero and every column $C_j=(a_{ij}\mid i\in \nnn_0)$ tends to $\infty$.

13.57 DO   ASY 3.23 (limit of non-decreasing sequences)

13.61 XC (5 points)   ASY 3.26   ($s_{n+1}=\sqrt{2}^{s_n}$)

13.63 XC (5 points)   ASY 3.27   ($t_{n+1}=c^{t_n}$)

13.65 STUDY   ASY Facts 3.24 and 3.25   ($\lim (1+z/n)^n$)

13.69 XC (4 points)   ASY 3.28   ($\lim F_{n+1}/F_n$)

13.XX  

13.81 STUDY   ASY Chap. 4 (upper/lower limits)

13.83 DO   all exercises in ASY Chap. 4

13.87 HW (3 points)   ASY 4.9   (when is $\sup(S) < \inf(S)$ ?)

13.89 HW (4 points)   ASY 4.23   (limsup and liminf of $(-1)^n (1+1/n)$)

13.91 HW (3 points)   ASY 4.26   (find bounded sequences s.t. $\limsup(a_n+b_n) < \limsup a_n + \limsup b_n$)

13.XX  

13.101 STUDY   Review matrix multiplication.

13.103 HW (4 points)   Consider the $2\times 2$ matrix   $A= \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \,.$   For $k\ge 1$, prove: $$A^k= \begin{pmatrix} F_{k+1} & F_k \\ F_k & F_{k-1} \end{pmatrix} \,.$$

12.15 TERMINOLOGY   The canonical form of the complex number $z$ is $z=a+bi$ where $a,b\in\rrr$ and $i$ is a symbol that by definition satisfies the equation $i^2=-1$. We call $a$ the real part of $z$ and $b$ the imaginary part of $z$. (So the imaginary part is a real number.) The absolute value of $z$ is $|z|=\sqrt{a^2+b^2}$. The polar form of $z$ is a representation of $z$ in the form $z=r(\cos \theta + i \sin\theta)$ where $r,\theta$ are real numbers and $r\ge 0$. It follows that $r=|z|$. (Why?) Moreover, $a =r\cos\theta$ and $b=r\sin\theta$. The angle $\theta$ (given in radians) is called an argument of $z$. Every complex number has infinitely many arguments. For $z=0$, every real number is an argument. If $z\neq 0$ and $\theta$ is an argument of $z$ then the set of all arguments of $z$ is $\{\theta + 2k\pi \mid k\in\zzz\}$.

12.21 HW (2+4+1 points)   Let $z=5+12i$ where $i^2=-1$.   (a)   Find the absolute value of $z$. Give its simplest expression.   (b)   Find an argument $\theta$ of $z$ such that $0 <\theta < \pi/2$. Describe $\theta$ to 3 digits accuracy (in radians). You may use a calculator only to compute the $\arccos$ and $\arcsin$ functions. These functions take real numbers as inputs. You may not use functionality that takes complex numbers as inputs. Describe your steps.   (c)   Find all arguments of $z$.

12.23 DEF   The conjugate of the complex number $z=a+bi$ is $\zbar = a-bi$.

12.25 DO   Verify:   (a)   $a=(z+\zbar)/2$   (b)   $b = (\zbar-z)i/2$   (c)   $z\zbar = |z|^2$   (d) if $z\neq 0$ then $1/z = \zbar/|z|^2$.

12.27 HW (2 points)   If $\theta$ is an argument of $z$, find an argument of $\zbar$.

12.31 FACT (multiplication of complex numbers given in polar form)   Let $z = r(\cos \alpha + i\sin\alpha)$ and $w= s(\cos\beta + i\cos\beta)$. Then $zw = rs(\cos(\alpha+\beta)+ i\sin(\alpha+\beta))$. In particular, $|zw|=|z|\cdot |w|$ and $\alpha + \beta$ is an argument of $z$.

12.33 DO   Observe that $|z|=1$ if and only if $z$ can be written as $z=\cos\theta + i\sin\theta$ for some $\theta\in\rrr$.

12.35 DO   Observe that $|z|=1$ if and only if $1/z = \zbar$.

12.37 DO   For $n\in \nnn$, if $\theta$ is an argument of $z$ then $n\theta$ is an argument of $z^n$.

12.XX  

12.41 DEF   For $n\in\nnn$, the complex number $z$ is an $n$-th root of unity if $z^n = 1$.

12.43 DO   Prove: if $z$ is an $n$-th root of unity then   (a)   $|z|=1$ and   (b)   if $\theta$ is an argument of $z$ then $\theta/\pi$ is a rational number.

12.XX  

12.XX  

12.51 DO   Find all $n$-th roots of unity, in canonical form, for $1\le n\le 4$. Remember that there are $n$ of them.

12.53 DO   Let $n\in\nnn$. Prove: the $n$-th roots of unity are precisely the numbers $cos\theta + i\sin\theta$ where $\theta = 2k\pi/n$ for $k=0,1,\dots,n-1$.

12.55 HW (2 points)   Prove: if $k,\ell\in \nnn$ (non-negative integers) and $k\mid \ell $ then every $k$-th root of unity is also an $\ell$-th root of unity.

12.59 HW (3 points)   Let $\omega_0=1$, $\omega_1$, and $\omega_2$ denote the three third roots of unity. Prove that the 6-th roots of unity are the third roots of unity and their negatives, i.e., $\pm \omega_0$, $\pm \omega_1$, $\pm \omega_2$.

12.63 HW (6 points)   Prove that for $n\ge 2$, the sum of the $n$-th roots of unity is $0$.

12.65 DO   Prove: $x^n-1 = \prod_{k=0}^{n-1} (x-\omega_k)$ where $\omega_k = \cos(2k\pi/n) + i \sin(2k\pi/n)$.

12.68 DO   Verify the following exercise for $n=3, 4, 6$.

12.69 XC (6 points)   Let $n\ge 3$. Let $P_0,\dots,P_{n-1}$ be the vertices of a regular $n$-gon inscribed in a unit circle. Prove: $\prod_{k=1}^{n-1} \overline{P_0P_k}=n$, where $\overline{AB}$ denotes the length of the segment connecting the point $A$ to the point $B$.

12.XX  

12.XX  

12.81 STUDY   the handout "Asymptotic Equality and Inequality" (ASY), Section 1 (Sequences) and Section 3 (Limits).

12.85 HW (2 points)   ASY 3.5(b) (define negative infinite limit)

12.100 Answer to 13.15   The negation of the statement that "the sequence $(a_n)$ is eventually non-zero" is
    "$a_n$ is infinitely often zero"

12.XX  

12.XX  

More to follow. Please check back later.

11.12 NOTATION   Recall the notation $[n]=\{1,2,\dots,n\}$ where $n$ is a non-negative integer. Examples: $[3]=\{1,2,3\}$, $[1]=\{1\}$, $[0]=\emptyset$.
For a set $A$ and a non-negative integer $k$, recall the notation $\binom{A}{k}$ for the set of $k$-subsets of $A$. Note that, by definition, $\left|\binom{A}{k}\right| = \binom{|A|}{k}$.

11.15 DEF   The function $f:[k]\to [m]$ is (strictly) monotone increasing if $(\forall i\in [k-1])(f(i) < f(i+1))$. We shall omit the words "strictly" and "monotone" and just refer to such functions as "increasing" functions. Let $\INCR(k,m)$ denote the set of increasig functions $f:[k]\to [m]$ and let $\incr(k,m)=|\INCR(k,m)|$.
The function $g:[k]\to [m]$ is monotone nondecreasing if $(\forall i\in [k-1])(f(i) \le f(i+1))$. We shall omit the word "monotone." Let $\NONDECR(k,m)$ denote the set of nondecreasing functions $f:[k]\to [m]$ and let $\nondecr(k,m)=|\NONDECR(k,m)|$.

11.18 DO   Determine the quantity $\incr(k,m)$. (Done in class.)
The answer is $\binom{m}{k}$ and the proof consists in establishing a bijection between the set $\INCR(k,n)$ and the set $\binom{[m]}{k}$.

11.20 DO   Prove: $\nondecr(k,m)=\incr(k,m+k-1)$. (Done in class.)
The proof is a bijection between the sets $\NONDECR(k,m)$ and $\INCR(k,m+k-1)$: to every function $f\in \NONDECR(k,m)$ assign the function $g\in\INCR(k,m+k-1)$ defined as follows:
    for $i\in [k]$, let $g(i) = f(i) + (i-1)$.
Show that this assignment is indeed a bijection between the two sets above.

11.21 DO   Observe the corollary to the preceding exercise: $$\nondecr(k,m)= \binom{m+k-1}{k}$$

11.23 HW (4+4+4 points)   Let $\ell, m \ge 1$. Consider the equation
   $(*)$     $\sum_{i=1}^{\ell} x_i = n$   (a) Count the solutions to the equation in positive inters $x_i$.
Give a bijective solution: prove that the number of solutions is equal to $\incr(k,m)$ for certain values of $k$ and $m$. State the appropriate values of $k$ and $m$ in terms of $\ell$ and $n$.
  (b) Count the solutions to equation $(*)$ in non-negative inters $x_i$. Give two bijective solutions:
  (b1)   Design a bijection between the set of solutions to (b) and the set of solutions to (a) with modified parameters. State the vales $\ell_a$ and $m_a$ you use in (a) in terms of $\ell$ and $m$.   (b2)   Design a bijection between the set of solutions to (b) and $\NONDECR(k,m)$ for certain values of $k$ and $m$. State the appropriate values of $k$ and $m$ in terms of $\ell$ and $n$.
Your answers should be simple binomial coefficients.

11.25 HW (3+3 points)   Let $h,q \ge 1$. Consider the inequality
   $(**)$     $\sum_{i=1}^{h} y_i \le q$.
  (a) Count the solutions to the inequality in positive integers $y_i$.
  (jb) Count the solutions to the inequality in non-negative integers $y_i$.
Give bijective solutions, in each case reducing the question to the corresponding case of equation $(*)$ above.

11.27 HW (4 points)   Count the functions $h:[k]\to [m]$ that satisfy the condition $(\forall i\in [k-1])(f(i+1)\ge f(i)+2)$. Give a bijective solution, using 11.18. Your answer should be a simple binomial coefficient.

11.XX  

11.49 STUDY   DMmini Terminology 6.1.42, especially legal coloring, $k$-colorability, chromatic number.

In the exercises below, $\chi(G)$ denotes the chromatic number of the graph $G=(V,E)$ with $n\ge 1$ vertices. $H$ is another graph.

11.51 DO   Observe that $\chi(G)=1 \Leftrightarrow E=\emptyset$.

11.53 DO   Observe:  if $H\subseteq G$ then $\chi(H)\le \chi(G)$.

11.55 DO   Observe:  $G$ is $k$-colorable if and only if $\chi(G) \le k$.

11.57 DO   Observe:  $G$ is 2-colorable if and only if $G$ is bipartite.

11.59 DO   Let $n\ge 3$. Prove: if $n$ is even then $\chi(C_n)=2$ and if $n$ is odd then $\chi(C_n)=3$.

11.61 HW (4 points)   Prove: every tree is bipartite.

11.63 XC (5 points)   Prove: $G$ is bipartite if and only if $G$ contains no odd cycle.
The $\Rightarrow$ direction is immediate by the preceding exercise. Prove the $\Leftarrow$ direction only. First, solve the case when $G$ is connected; use a spanning tree.

11.65 DO   Observe:  $\chi(G) \le n$. Moreover, $\chi(G)=n$ of and only if $G \cong K_n$.

11.67 XC (5+5 points)   (a)   Prove:   $\chi(G)\cdot\chi(\Gbar)\ge n$.
  (b)   If $n=k\ell$ then there exists a graph $G$ with $n$ vertices such that $\chi(G)=k$ and $\chi(\Gbar)=\ell$.

11.69 HW (6 points)   Find a graph $G$ such that $\chi(G)=4$ but $G$ does not contain a 4-clique, i.e., no subgraph of $G$ is isomorphic to $K_4$. Make $n$ as small as possible.
You do not need to prove that your graph is smallest but prove that (a) $G$ does not cotain a 4-clique and (b) its chromatic number is 4. In proving (b), make sure to prove that (b1)   $\chi(G)\le 4$ and that (b2)   $\chi(G)\ge 4$. Clearly structure your proof: before each part of the proof, state what you are about to prove.

11.71 HW (4 points)   Let $\Delta$ denote the maximum degree of the graph $G$, i.e., $\Delta = \max_{x\in V} \deg(x)$. Prove:   $\chi(G) \le 1+\Delta$.

11.XX  

11.81 DEF   Let $G=(U,E)$ and $H=(W,F)$ be graphs. We define the Cartesian product graph $K=G\Box H$ by setting $V(K)=U\times W$ and defining $(u_1,w_1)\sim_K (u_2,w_2)$ if either ($u_1=u_2$ and $w_1\sim_H w_2$) or ($w_1=w_2$ and $u_1\sim_G u_2$).   (Here $v_i\in V$ and $w_i\in W$.)

11.83 DEF/DO   (a)   For $k,\ell\ge 1$, we define the $k\times \ell$ grid graph as $P_k\Box P_{\ell}$.

                

The picture shows the $4\times 7$ gride graph.
The $k\times \ell$ grid graph has $n=k\ell$ vertices. Count its edges. How many vertices have degree less than 4 ?
  (b)   For $k,\ell\ge 3$, we define the $k\times \ell$ toroidal grid graph as $C_k\Box C_{\ell}$.

                

It has $n=k\ell$ vertices. It is regular of degree 4. Count its edges.
  (e)  For $k,\ell\ge 1$ we define the $k\times\ell$ rook graph as $K_k\Box K_{\ell}$.
  (d)   Show that for $d\ge 1$ the $d$-dimensional cube graph $Q_d$ is the $d$-th Cartesian power of $K_2$, i.e. $$ Q_d = \underbrace{K_2\Box K_2\Box\cdots\Box K_2}_{d\text{ times}}$$

11.85 HW (5 points)   determine the chromatic number of the $k\times\ell$ rook graph.

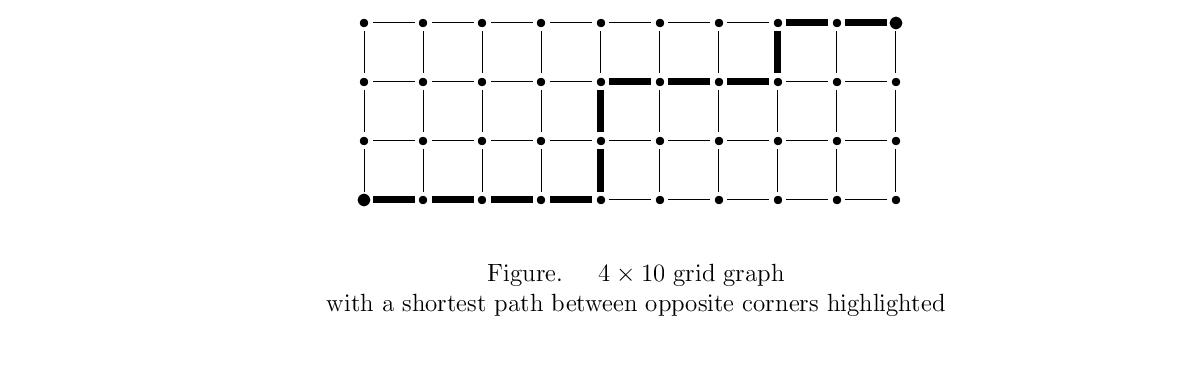
11.87 HW (4 points)   DMmini 6.1.49 (count the shortest paths between opposite corners of the $k\times\ell$ grid). The answer should be a simple closed-form expression. For our definition of closed-form expressions, read PROB Chap. 7.1.

11.XX  

More to follow. Please check back later.

10.10 DEFINITION   Recall that for $n,k\ge 0$, the quantity $\binom{n}{k}$ counts the $k$-subsets of an $n$-set.

10.12 DO   (a)   If $k > n$ then $\binom{n}{k}=0$
  (b)   $\binom{n}{0}=\binom{n}{n}=1$
  (c)   $\binom{n}{k}=\binom{n}{n-k}$
  (d)   $\binom{n}{1}=\binom{n}{n-1}=n$

10.13   $\binom{n}{k} = \frac{n(n-1)\cdots (n-k+1)}{k!}$

10.15 (Binomial Theorem)   $$ (x+y)^n = \sum_{k=0}^n \binom{n}{k}x^k y^{n-k} $$

10.17 DO   Review the proof of the Binomial Theorem.

10.19 DO   (Most useful form of the Binomial Theorem) $$ (1+x)^n = \sum_{k=0}^n \binom{n}{k}x^k $$

10.21 DO   Give a combinatorial proof of Pascal's Identity (3.32).
Hint.   Count the $(k+1)$-subsets of an $(n+1)$-set by declaring an element of the $(n+1)$-set special, and count separately those $(k+1)$-subsets that include the special element and those that don't.

10.23 DO   Give an algebra proof of Pascal's Identity.
Hint.   Use 10.19. Note that $(1+x)^{n+1}=(1+x)^n\cdot (1+x)$. Compare the coefficients of $x^{k+1}$ on each side.

10.25 HW (4+4 points)   Let $S_n = \sum_{j=5}^n \binom{j}{5}$. Prove:   $S_n = \binom{n+1}{6}$. Give two proofs:
  (a)  By induction on $n$. Use Pascal's Identity.
  (b)  Give a combinatorial proof (show that the two sides count the same objects).

10.27 HW (Vandermonde's Identity) (5+5 points)   Prove: $\sum_{k=0}^n \binom{n}{k}^2 = \binom{2n}{n}$.
Give two proofs: (a) a combinatorial proof (b) an algebra proof: use the Binomial Theorem in its "most useful form" (10.19): observe that $(1+x)^n\cdot (1+x)^n = (1+x)^{2n}$, and compare the coefficients of $x^n$ on each side.

10.29 DO   Prove: $\sum_{k=0}^n \binom{n}{k} = 2^n$.
Give two proofs: (a) a combinatorial proof, using the fact that an $n$-set has $2^n$ subsets (we gave a bijective proof of this fact), and (b) an algebra proof (expand $(1+1)^n$ using the Binomial Theorem, most useful form).

10.31 HW (4 points)   Let $E_n$ denote the number of even-sized subsets of an $n$-set, and $O_n$ the number of odd-sized subsets of an $n$-set. Give a combinatorial (bijective) proof that for $n\ge 1$ we have $E_n = O_n$.
Note. In class we gave an algebra proof: we expanded the expression $(1-1)^n$ using the Binomial Theorem, most useful form.

10.33 DO   Infer from the preceding exercise that $$ \sum_{k=0}^{\infty} \binom{n}{2k} = 2^{n-1} $$ Note that this is not really an infinite sum: all terms with $k > n/2$ are zero.

10.35 DO   Let $S(n,k) = \sum_{t=0}^{\infty} \binom{n}{tk}$.   Prove:   $(\forall n\ge 0)(S(n,3)\neq 2^n/3)$.

10.37 XC (8 points)   Prove: $$ \left|S(n,3) - \frac{2^n}{3}\right| < 1.$$ Use the Binomial Theorem, most useful form, with $x$ a complex third root of unity.

10.41 XC (4+1)   Let $g_n$ denote the number of non-isomorphic graphs with $n$ vertices. Prove: $$ \frac{2^{\binom{n}{2}}}{n!} \le g_n \le 2^{\binom{n}{2}} $$

10.43 HW (4 points)   Let $p$ be a prime number and $1\le k\le p-1$. Prove that $\binom{p}{k}\equiv 0 \pmod{p}$. Explicitly use Euclid's Lemma (5.84).

10.XX  

10.XX  

10.XX  

More to follow. Please check back later.

9.19 DEF   A pendant vertex in a graph is a vertex of degree 1.

9.21 DO   Prove: every tree of order $n\ge 2$ has a pendant vertex.
Hint.   Let $P$ be a longest path in the tree. Prove that the endpoints of $P$ have degree 1 in the tree. (Done in class, review.)

9.23 TERMINOLOGY   If $e=\{x,y\}$ is an edge of the graph $G$ then we say that the vertex $x$ and the edge $e$ are incident.

9.25 NOTATION   If $G$ is graph and $x\in V(G)$ then $G-x$ denotes the subgraph obtained from $G$ by removing the vertex $x$ and all edges incident with $x$.
Example. $C_k -x \cong P_{k-1}$.

9.27 HW (5 points)   Let $T$ be a tree of order $n\ge 2$ and let $x$ be a pendant vertex of $T$. Prove: $T-x$ is a tree.

9.29 DO   Prove: a tree of order $n\ge 1$ has size $m=n-1$.
Proof by induction on $n$, using 9.21 and 9.27. Done in class. (Review!)

9.31 DO   Prove that a graph $G$ is a tree if and only if $(\forall x,y\in V(G))(\exists ! x\dots y$ path$)$.

9.33 DEF   A spanning tree of a graph $G$ is a spanning subgraph that is a tree.

9.35 DO   Prove: the graph $G$ has a spanning tree if and only if $G$ is connected.

9.37 FACT (Kirchhoff, 1948)   The number of spanning trees of the graph $G$ can be expressed as the determinant of a matrix associated with $G$.

9.39 FACT (Cayley's formula)   The number of spanning trees of $K_n$ is $n^{n-2}$.

9.51 HW (4 points)   Let $G$ be a regular graph of degree $d$ and order $n$. Count the walks of length $k$ in $G$. Your answer should be a simple closed-form expression in terms of $n,d$, and $k$.

More to follow. Please check back later.

Material covered.   Subgraph, spanning subgraph, induced subgraph. Accessibility, connected components. Path, walk. Forest, tree.

8.10 DEF   The sequence of Fibonacci numbers is defined by the Fibonacci recurrence $ F_n = F_{n-1}+F_{n-2}$ (for $n\ge 2$) and the initial values $F_0=0$ and $F_1=1$.
So $F_0=0, F_1=1, F_2=1, F_3=2, F_4=3, F_5=5, F_6=8, F_7=13, F_8=21, F_9 = 34, F_{10}=55, F_{11}=89, F_{12}=144, \dots$.

8.11 DO   Prove:   $(\forall n\ge 0)(F_n < 2^n)$.

8.13 XC (4 points)   Prove:   $(\forall n\ge 6)(F_n \ge 2^{n/2})$.

8.15 XC (4 points)   Prove:   $(\forall n\ge 2)(F_{n+2}=3\cdot F_{n} - F_{n-2})$.

8.17 HW (4 points)   $(\forall n\ge 1)(F_n^2-F_{n+1}F_{n-1}=(-1)^{n+1})$.

8.19 XC (5 points)   For $n\ge 0$ we have $$\sum_{k=0}^{\lfloor n/2\rfloor} \binom{n-k}{k} = F_{n+1}\,.$$

8.20 DEF   The integers $a$ and $b$ are relatively prime if $\gcd(a,b)=1$.
For example, 15 and 28 are relatively prime, but 15 and 27 are not.

8.23 FACT (generalization of Euclid's lemma)   If $k\mid bc$ and $k$ and $b$ are reatively prime then $k\mid c$.

8.25 DO   If $1\le k\le n$ then $\displaystyle{\binom{n}{k}=\frac{n}{k}\binom{n-1}{k-1}}\,.$

8.27 XC (4 points)   If $n\ge 0$ then $\binom{2n}{n}$ is divisible by $n+1$.

8.29 DO   This problem has been canceled (identical with 3.40).

8.31 XC   This problem has been canceled (identical with 3.42).

8.XX  

8.36 TERMINOLOGY   The order of a graph is the number of its vertices $(n)$, and the size of the graph is the number of its edges $(m)$.
Examples:   the order of $K_n$ is $n$, and the size of $K_n$ is $\binom{n}{2}$. The order of $P_n$ is $n$, and its size is $n-1$.

8.38 HW (4 points)   Prove that the maximum size of a bipartite graph of order $n$ is $\lfloor n^2/4\rfloor$.

8.40 STUDY   DMmini Terminology 6.1.16: subgraphs, spanning subgraphs, induced subgraphs.

8.41 DO   DMmini 6.1.17-6.1.19.

8.43 HW (3 points)   DMmini 6.1.20 (counting spanning subgraphs of $K_n$ of a given size). No proof required.

8.45 XC (12 points)   DMmini 6.1.21 (counting subgraphs of $P_n$).

8.47 HW (4 points)   Count the 4-cycles (copies of $C_4$) in the complete bipartite graph $K_{r,s}$. Your answer should be a simple closed-form expression in terms of $r$ and $s$.

8.49 HW (3+3 points)   (a) Find two non-isomorphic regular graphs of the same order and size. Make the size as small as possible. Prove that your graphs are not isomorphic.   (b) Same as (a) but both graphs should be connected.
You do not have to prove, in either problem, that the size of your graphs is minimal.

8.51 HW (13 points)   Draw all non-isomorphic trees of order 7. State, how many trees you got. You lose 3 points for each mistake: a pair of isomorphic trees, a tree missed, one of your graphs is not a 7-vertex tree.

8.53 HW (4 points)   Let $G$ be a graph. Prove that $G$ or its complement, $\Gbar$, is connected.

More to follow. Please check back later.

6.XX  

6.20 DEF   A predicate on the set $A$ is a function from $A$ to a binary codomain such as $\{0,1\}$ of $\{N,Y\}$ (No,Yes) or $\{F,T\}$ (False,True).

6.22 DO   Let $|A|=n$. Count the predicates on $A$.
(Answer: $2^n$. Why?)

6.25 DEF   The Cartesian product of the sets $A$ and $B$ is the set $A\times B=\{(a,b)\mid a\in A, b\in B\}$ (the set of ordered pairs formed by an element of $A$ and an element of $B$).

6.27 FACT   $|A\times B|=|A|\cdot|B|$.
This is not a theorem but the definition of multiplication of natural numbers.

6.29 DEF   A relation from $A$ to $B$ is a predicate on $A\times B$. We say that $A$ is the domain and $B$ is the codomain of the relation.

6.31 DO   Let $|A|=m$ and $|B|=k$. Count the relations from $A$ to $B$.
(Answer: $2^{mk}$. Why?)

6.33 NOTATION   Rather than writing $R(a,b)=T$, we write $aRb$. Examples: $a\le b$ (instead of "$\le(a,b)=T$"), $a\mid b$, etc.

6.35 DEF (homogeneous relation)   A relation on $A$ is a relation from $A$ to $A$. We call such relations homogeneous.

In the following sequence of definitions and exercises, $R$ is a relation on the set $A$ where $|A|=n$. Your answer to each counting problem should be a simple closed-form expression.

6.37 DEF   $R$ is reflexive if $(\forall x\in A)(xRx)$.

6.39 DEF   $R$ is irreflexive if $(\forall x\in A)(x{\not R}x)$, i.e., $(\forall x\in A)(\neg(xRx))$.

6.41 HW (4 points) (a) Count the reflexive relations on $A$.   (b) Count the irreflexive relations on $A$.

6.43 DO   Assume the relation $R$ is both reflexive and irreflexive. Prove: $A=\emptyset$.

6.45 DEF   $R$ is symmetric if $(\forall x,y\in A)(xRy \Rightarrow yRx)$.

6.47 HW (3+3 points)   (a) Count the symmetric relations on $A$.   (b) Count the symmetric irreflexive relations on $A$.

6.49 DEF   $R$ is transitive if $(\forall x,y,z\in A)((xRy\wedge yRz) \Rightarrow xRz)$.

6.51 XC (4 points)   Count those relations on $A$ that are irreflexive, symmetric, and transitive.

6.53 DEF   $R$ is an equivalence relation if $R$ is reflexive, symmetric, and transitive.

6.55 DO   Find important examples of relations that are reflexive and transitive but not symmetric.
Some answers: divisibility of integers, $\le$ relation among integers, subset relation in the powerset.

6.57 STUDY   REAS22 6.135 (examples of equivalence relations)

6.59 STUDY   REAS22 6.140-6.155 (partitions vs. equivalence relations, culminating in the Fundamental Theorem of Equivalence Relations (REAS22 6.150)

6.61 STUDY   REAS22 6.137:  the role of equivalence relations in concept formation.

6.63 STUDY   REAS22 7.38-7.42 (partitions vs. equivalence relations)

6.65 STUDY   REAS 7.45 (steps of the proof of the Fundamental Theorem of Equivalence Relations (REAS22 6.150)

6.67 DO   REAS 7.47 (DO proofs of these steps)

6.69 XC (4 points)   REAS 7.50 (key step of the proof)

In the following sequence of exercises, our universe is $\zzz$.

6.71 DEF (residue classed mod $m$)   REAS 7.55

6.73 HW (2+2+2+2 points)   REAS 7.57 (residue classes modulo $2$, $-3$, $1$, $0$)

6.75 HW (3 points)   If $a\equiv x\pmod m$ and $b\equiv y\pmod m$ then $a+b\equiv x+y \pmod m$. State, what property of divisibility you are using.

6.77 DO If $a\equiv x\pmod m$ and $b\equiv y\pmod m$ then $a-b\equiv x-y \pmod m$. State, what property of divisibility you are using.

6.79 HW (3 points) If $a\equiv b\pmod m$ and $c\in\zzz$ then $ac\equiv bc \pmod m$. State, what property of divisibility you are using.

6.81 HW (4 points)   If $a\equiv x\pmod m$ and $b\equiv y\pmod m$ then $ab\equiv xy \pmod m$. To make this proof elegant, do not use any properties of divisibility, just use already proven properties of congruences. State, what properties of congruences you are using. Elegance counts.

5.20 FACT (Pigeon Hole Principle)   An $A\to B$ injection exists if and only if $|A|\le |B|$.

5.23 FACT   An $A\to B$ surjection exists if and only if $|A|\ge |B|$.

5.25 TERMINOLOGY   Given two sets, $A$ and $B$, suppose we want to prove that $|A|\le |B|$. An injective proof of this statement means the construction of injection $A\to B$. A surjective proof of the same statement means the construction of a surjection $B\to A$.

5.30 DEF (bijection)   A function $f\in B^A$ is a bijection if $f$ is invertible, i.e., there exists a functions $g\in A^B$ such that $(\forall x\in A)(g(f(x))=x)$ and $(\forall y\in B)(f(g(y))=y)$.

5.32 DO   Prove: a function $f\in B^A$ is a bijection if and only if $f$ is both an injection and a surjection.

5.34 FACT   An $A\to B$ bijection exists if and only if $|A|=|B|$.

5.36 TERMINOLOGY   Given two sets, $A$ and $B$, suppose we want to prove that $|A| = |B|$. An bijective proof of this statement means the construction of a bijection $A\to B$.

5.38 DEF   A permutation of a set $A$ is an $A\to A$ bijection.

5.40 DO   If $|A|=|B|=n$ then the number of $A\to B$ bijections is $n! = n(n-1)\cdot\dots\cdot 2\cdot 1$.

5.42 DEF (powerset)   Let $A$ be a set. The powerset of $A$, denoted $\calP(A)$, is the set of subsets of $A$: $$ \calP(A) = \{B \mid B\subseteq A\}\,.$$

5.44 DO   Let $|A|=n$. Prove: $|\calP(A)|=2^n$.
Instruction (discussed in class):  Give a bijective proof of the fact that $|\calP(A)| = |\{0,1\}^n|$.

5.50 DEF (divisibility)   We say that $a$ divides $b$ (notation: $a\mid b$) if $(\exists x)(ax = b)$.
Other verbal forms of the statement that $a\mid b$:
  $a$ is a divisor of $b$.
  $b$ is a multiple of $A$.
Examples:   $37\mid 999$. Proof: Take $x=27$.
       $0\mid 0$. Proof: Take $x=42$. (Or take $x=0$. Or any other integer.)

5.53 DO (additivity of divisibility)   Assume $a\mid x$ and $a\mid y$. Prove: $a\mid x+y$ and $a\mid x-y$. State, what property of arithmetic we are using in the proof.
Proof: discussed in class. The property of arithmetic we use is distributivity.

5.55 DO (transitivity of divisibility)   Let $a\mid b$ and $b\mid c$. Then $a\mid c$. What property of arithmetic is used in the proof?
(The property we use is associativity of multiplication.)

5.57 NOTATION   We write $\Div(n)$ to denote the set of divisors of $n$: $$ \Div(n) = \{k : k\mid n\}$$ Examples: $\Div(6) = \{\pm 1, \pm 2, \pm 3, \pm 6\}$,      $\Div(1) = \{\pm 1\}$.

5.59 DO   $\Div(0) = \zzz$.

5.61 DO   Dmini 4.1.2:   $\Div(a)\subseteq \Div(b) \Leftrightarrow a\mid b$

5.62 DO   Dmini 4.1.3:   $\Div(a) = \Div(b) \Leftrightarrow a = \pm b$

5.64 DO   $(\forall x)(a\mid x) \Leftrightarrow a=\pm 1$

5.66 DO   $(\forall x)(x\mid a) \Leftrightarrow a=0$

5.70 DEF (congruence)   Dmini "Congruence notation" after 4.1.3.

5.72 DO   Let us fix $m$. Prove that congruence modulo $m$ is
   (a) reflexive, i.e., $(\forall x)(x\equiv x \pmod m)$, and
   (b) symmetric, i.e., $(\forall x,y)\left((x\equiv y \pmod m) \Rightarrow (y\equiv x\pmod m)\right)$

5.73 HW (4 points)   (continued) (c) transitive:
$$(\forall x,y,z)\left((x\equiv y \pmod m) \wedge (y\equiv z \pmod m) \Rightarrow (x\equiv z\pmod m)\right)\,.$$ State what property of divisibility you are using in the proof.

5.78 HW (4 points)   If $x$ is odd then $x^2\equiv 1 \pmod{8}$.

5.79 DEF   $p$ is a prime number if $|\Div(p)|=4$.

5.80 HW (4 points)   If $p$ is a prime number and $p\ge 5$ then $p\equiv\pm 1 \pmod{6}$.

5.82 DEF (prime property)   We say that the number $k$ has the prime property if $(\forall a, b)(k\mid ab \Rightarrow (k\mid a \vee k\mid b))$

5.84 THEOREM (Euclid's Lemma)   Every prime number has the prime property.

5.86 DO   $6$ does not have the prime property.

5.88 XC (4 points)   Find all numbers that have the prime property.

5.90 XC (4 points)   If $p$ is a prime number and $x^2\equiv 1 \pmod p$ then $x\equiv \pm 1 \pmod p$.

More to follow. Please check back later.

Material covered.   Closed-form expression. Factorials. Counting injections. Range of a function. Counting surjections $A\to B$ where $|B|=2$ and $|B|=3$. Naive probability. Sample space, event. Example: poker hand. Probability of "full house." Example: flipping $n$ coins. Probability that $k$ of the coins come up "Heads." Partitions, Bell numbers.

4.20 DEF (naive probability)   Let $\Omega$ be the set of possible outcomes of an experiment (say, dealing 5 cards from the standard deck of 52 cards: a poker hand). We refer to $\Omega$ as the sample space. Every subset of $\Omega$ is called an event. The (naive) probability of the event $A\subseteq\Omega$ is defined as $$P(A) = \frac{|A|}{|\Omega|}$$ (number of "good outcomes" (of the experiment) divided by the total number of possible outcomes).

4.25 DO   Study the standard deck of cards. Study various types of poker hands (four of a kind, flush, full house, two-pair, etc.) and calculate the probability of each type.

4.28 DO   $P($full house$)= \frac{13\cdot 12\cdot 4\cdot 6}{\binom{52}{5}}$

4.30 DO   We flip $n$ coins. The probability that $k$ of the come up "Heads" is $\frac{\binom{n}{k}}{2^n}$.

4.33 DEF (partitions, Bell numbers)   REAS22 6.90-6.92.

4.35 DO   REAS22 6.95

4.36 HW (4 points)   Give an injective proof that $B(n) \le n!$. Give an injection from the set of partitions of $[n]$ to the set of permutations of $[n]$.
(Here $[n]=\{1,2,\dots,n\}$.)

4.XX HW  

More to follow. Please check back later.

3.20 DEF   Let $\Sigma$ be a finite set; we shall refer to $\Sigma$ as the alphabet; we shall call the elements of $\Sigma$ "letters." A string of length $n$ over $\Sigma$ is a sequence $a_1a_2\dots a_n$ where $a_i\in\Sigma$. We denote the set of all strings of length $n$ over $\Sigma$ by $\Sigma^n$. A $(0,1)$-string is a string over the alphabet $\{0,1\}$. Example:  $\{a,x\}^3 = \{aaa,aax,axa,axx,xaa,xax,xxa,xxx\}$.

3.22 DO   Let $\Sigma$ be an alphabet of size $k$. Then $|\Sigma^n| = k^n$.

3.24 XC (4 points)   Let $W_n\subseteq \{0,1\}$ denote the set of those $(0,1)$-strings of length $n$ that do not contain consecutive 1s.
Example:  $W_4=\{0000,0001,0010,0100,0101,1000,1001,1010\}$.
Determine $|W_n|$. Express your answer in terms of a familiar sequence.

3.26 DO   Let $\Sigma$ be an alphabet of size $k$. Then the number of strings of length $n$ over $\Sigma$ consisting of distinct letters is $k(k-1)\dots (k-n+1)=\prod_{i=0}^{n-1} (k-i)$.
This statement is valid even if $k < n$; in this case, the product is zero because one of its terms is $0$.
If $k\ge m$ then this quantity can also be written as $\frac{k!}{(k-m)!}$.

3.28 DEF   Let $n,k\ge 0$. An $n$-set is a set of $n$ elements. $\binom{n}{k}$ denotes the number of $k$-subsets of an $n$-set.

3.30 DO   (a)   If $k > n$ then $\binom{n}{k}=0$.
  (b)   $\binom{n}{0} = \binom{n}{n} = 1$.
  (c)   For $0\le k\le n$ we have $\binom{n}{k}=\binom{n}{n-k}$.

3.32 DO (Pascal's Identity)   If $n,k\ge 0$ then $$ \binom{n+1}{k+1} = \binom{n}{k}+\binom{n}{k+1}\,.$$

3.34 DO   For $n,k\ge 0$ we have $$\binom{n}{k} = \frac{n(n-1)\dots(n-k+1)}{k!}$$.

3.36 HW (4 points)   For $1\le k\le n$ we have $\displaystyle{\binom{n}{k} \ge \left(\frac{n}{k}\right)^k}$

3.38 DO   Prove:   $\displaystyle{n! \ge \left(\frac{n}{\eee}\right)^n}$.   Here $\eee=2.71\dots$ is the base of the natural logarithm. Use the power-series expansion $\eee^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}$.

3.40 DO   For $1\le k\le n$ we have   $\binom{n}{k} \le \frac{n^k}{k!}$.

3.42 XC (4 points)   For $1\le k\le n$ we have $\displaystyle{\binom{n}{k} \le \left(\frac{n\eee}{k}\right)^k}$.

More to follow. Please check back later.

Material covered   Membership relation: $x\in A$ means the element $x$ belongs to the set $A$. Set notation, setmaker bar, equality of sets, subset, definition of union, intersection, quantifiers, negation of quantified statement, negation of implication, divisibility.

2.10 DEF (equality of sets, defined in terms of the membership relation)   The sets $A$ and $B$ are equal if $$(\forall x)((x\in A)\leftrightarrow(x\in B)\}$$

2.11 DEF (subset)   $A$ is a subset of $B$ (notation: $A\subseteq B$ or $B\supseteq A$) if $$(\forall x)((x\in A)\rightarrow(x\in B)\}$$

2.12 DO   $A=B \Leftrightarrow (A\subseteq B) \wedge (A\supseteq B)$
("$\wedge$" denotes "AND")

2.13 DO   Define $A\not\subseteq B$ in terms of the membership relation.

2.14 DEF (union, intersection) $$A\cup B = \{x\mid (x\in A) \vee (x\in B)\}$$ ("$\vee$" denotes "OR") $$A\cap B = \{x\mid (x\in A) \wedge (x\in B)\}$$

In the following sequence of exercises, $A$ and $B$ are sets, $|A|=m$ and $|B|=k$. Recall that the set of functions with domain $A$ and codomain $B$ is denoted $B^A$.

2.15 DEF (collision)   Let $f\in B^A$ be a function. We say that the pair $\{u,v\}$ of distinct elements of $A$ collide under $f$ if $f(u)=f(v)$. In this case, the pair $\{u,v\}$ represent a collision. We write $\coll(f)$ to denote the number of collisions of $f$.

2.16 DO   Prove: if $|A|=m$ then $0\le \coll(f) \le m(m-1)/2$.

2.17 DEF (injection)   The function $f\in B^A$ is an injection if $\coll(f)=0$.

2.18 DEF (range)   The range of a function $f\in B^A$ is the set $\range(f)=\{f(x)\mid x\in A\}$. Note that $\range(f)\subseteq B$.

2.19 DEF (surjection)   The function $f\in B^A$ is a surjection if $\range(f)=B$.

2.20 DO       $|B^A| = k^m$. Recall the proof from class.

2.21 HW (4 points)   Count the injections $A\to B$. Give a simple formula in terms of $m$ and $k$.

2.22 HW (4 points)   Count the surjections $A\to B$ assuming $|B|=2$. Give a very simple formula in terms of $m$.

2.23 XC (4 points)   Count the surjections $A\to B$ assuming $|B|=3$. Give a simple formula in terms of $m$.