Graphs

Definition 2.1   A graph is a (finite) set $V$ of vertices, and a set $E$ of edges, where an edge is an unordered pair of vertices.

Definition 2.2   We say that a pair of vertices $v$ and $w$ are adjacent ($x\sim y$) if $\{v,w\}\in E$ and non-adjacent otherwise.

Definition 2.3   The neighbors of a vertex $v$ are the vertices adjacent to $v$.

Definition 2.4   If $G=(V,E)$, and $H=(W,F)$ are graphs, then we say that a function $f:V\to H$ is an isomorphism if $f$ preserves adjacency. That is, $x\sim y\Longleftrightarrow f(x)\sim f(y)$. If an isomorphism exists between two graphs, then we say they are isomorphic.

Definition 2.5   The degree of a vertex is the number of its neighbors.

Definition 2.6   A bipartite graph is a graph $(V,E)$ such that $V=V_1\dot{\cup} V_2$, where each edge contains exactly one element from each $V_i$.

Definition 2.7   A path of length $n$ in a graph is a sequence of distinct vertices, $(v_0,v_1,v_2,\dots, v_n)$ where $\{v_{i-1},v_{i}\}$ is an edge for all $i$.

Definition 2.8   A walk of length $n$ in a graph is a sequence of (not necessarily distinct) vertices, $(v_0,v_1,v_2,\cdots v_n)$ where $\{v_i,v_{i+1}\}$ is an edge for all $i$.

Definition 2.9   A cycle of length $n\ge 3$ in a graph is a walk $(v_0,v_1,v_2,\dots, v_n)$ where $v_0=v_n$ but otherwise there are no repeated vertices.

Remark 2.10   Notice that a path of length $n$ will have $n+1$ vertices, and a cycle of length $n$ will have $n$ vertices.

Notation 2.11   $P_n$ denotes the path on $n$ vertices and $C_n$ denotes the $n$-cycle (the cycle on $n$ vertices.

Definition 2.12   $K_n$ will be the complete graph on $n$ vertices, which is the graph such that for all $v\neq w$, $\{v,w\}$ is an edge of $K_n$.

Definition 2.13   $K_{k,\ell}$ will be the complete bipartite graph on $k+\ell$ vertices, which is the graph $(V\dot{\cup} W,E)$ such that $V$ and $W$ have $k$ and $\ell$ elements respectively, and $E=\{\{v,w\}\,:\,v\in V, w\in W\}$.

Definition 2.14   The distance between any two vertices is the length of the shortest path between them. The distance is infinite if no such path exists.

Definition 2.15   The diameter of a graph is the longest distance in the graph.

Definition 2.16   A graph is connected if there is a path between any two vertices.

Definition 2.17   The complement of a graph $G=(V,E)$ is the graph $\overline{G}=(V,\overline{E})$, where $E\cap \overline{E}=\emptyset$, and $E\dot{\cup}\overline{E}$ is the set of all $\binom{n}{2}$ pairs of vertices of $G$.

Remark 2.18   Notice that we have the following: $\overline{C_4}=2K_2$, $\overline{C_5}=C_5$, $\overline{P_3}=P_3$.

Exercise 2.19   If $G\cong \overline{G}$ then $n \equiv 0, 1 \mod 4$.

Definition 2.20   The girth of a graph is the length of the shortest cycle.

Definition 2.21   A tree is a connected graph with no cycles.

Remark 2.22   A tree has infinite girth.

Exercise 2.23   A tree with $n$ vertices has $n-1$ edges.

Exercise 2.24   Are the two graphs from the Petersen's graph handout isomorphic?

Theorem 2.25 (Handshake theorem)   $\sum_{v\in V} \deg(v)=2\vert E\vert$.

Theorem 2.26   If $G$ is a regular graph of degree $r$, and girth$(G)\geq 5$, then $n\geq r^2+1$.

In what cases is this bound tight, i.e. $n=r^2+1$? If $r=1$, then $K_2$ satisfies $n=r^2+1$. For $r=2$, $C_5$ satisfies this equation. For $r=3$, we have Petersen's graph. For $r=7$ there is a graph of degree $r$, girth 5, and $n=50$ vertices called the ``Hoffman-Singleton graph.''

Theorem 2.27 (Hoffman-Singleton)   If a regular graph of degree $r$ with $n=r^2+1$ vertices and girth at least $5$ exists then $r\in\{1,2,3,7,57\}$.

Remark 2.28   We have named such graphs with $r\in\{1,2,3,7\}$. It is not known whether such a graph with $r=57$ exists. It is, however, known that if such a graph exists, it cannot be quite as nice as the smaller ones: its automorphism group will not act transitively on its vertices, i.e., not all vertices will be equivalent under automorphisms (self-isomorphisms) of the graph (Aschbacher).

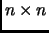
Definition 2.29   The adjacency matrix, $A_G=[a_{ij}]$, of a graph, $G$, is the $n\times n$ matrix such that $a_{ij}=1$ if $\{i,j\}$ is an edge of $G$, and 0 otherwise, where $n$ is the number of vertices.

Remark 2.30   Note that the diagonal and therefore the trace of the adjacency matrix is zero.

Theorem 2.31   If a graph is $r$-regular, then $r$ is an eigenvalue of its adjacency matrix.

Proof. The all-ones vector is an eigenvector for the adjacency matrix with eigenvalue $r$. $\qedsymbol$

Remark 2.32   $A_G$ is symmetric. Recall that this and the spectral theorem imply that it is diagonalizable over $\mathbb{R}$ with an orthonormal eigenbasis.

Exercise 2.33   If $G$ is a connected regular graph, then the multiplicity of $r$ as an eigenvalue is one (it is a simple eigenvalue).

Exercise 2.34   If $G$ is a regular graph of degree $r$ then the multiplicity of $r$ as an eigenvalue is the number of connected componenets of $G$.

Exercise 2.35   If $G$ is a regular graph and $\lambda$ is an eigenvalue of $G$ (i.e., an eigenvalue of $A_G$) then $\vert\lambda\vert\leq r$.

Exercise 2.36   If $G$ is a connected regular graph of degree $r$ then $-r$ is an eigenvalue if and only if $G$ is bipartite.