Extremal Set Theory

Theorem 0.10 (Dijen K. Ray-Chaudhuri, Richard M. Wilson)   Let $A_1,\dots,A_m\subseteq\{1,\dots,n\}$ be a set system satisfying

1. uniformity, i.e. $\vert A_i\vert=k$ for every $i$,
2. $s$ sizes of intersections, i.e. $\vert A_i\cap A_j\vert\in\{\ell_1,\dots,\ell_s\}$ for every $i\neq j$.

Then $m\leq \binom{n}{s}$.

Remark 0.11   For non-uniform set systems the above bound is tight. Simply take all sets of size at most $s$.

Remark 0.12   The original proofs were more involved and considered matrices of size $\binom{n}{s}\times\binom{n}{s}$. The matrix $M=(m_{i,j})_{m\times n}$, where $m_{i,j}=1$ if $j\in A_i$ and 0 otherwise, is called an incidence matrix of $A_1,\dots,A_m$.

Ray-Chaudhuri and Wilson used so-called higher incidence matrices for their proof.

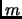
Definition 0.13   Inclusion Matrices. The $s$-inclusion matrix of the set system $A_1,\dots,A_m\subset [n]$ (where $[n]=\{1,\dots, n\}$) is an $m\times {n\choose s}$ matrix $M_s=(m_{i,j}^{(s)})$ is defined as follows: $i$ ranges from $1$ to $m$, $j$ ranges through the subsets of $[n]$ of size $s$, and $m_{i,j}^{(s)}=1$ if $j\subseteq A_i$, and 0 otherwise.

Ray-Chaudhuri and Wilson proved that $M_s$ has full row rank, i.e. $\mathop{\rm rk}\nolimits (M_s)=m$, by showing that $M_sM_s^t$ is a non-singular matrix.