


Next: Hypergraphs
Up: Discrete Math, 5th day,
Previous: Discrete Math, 5th day,
Notation:
![$ [k]=\{1,2,\ldots,k\}$](img1.gif) ;
;
![$ [k]^n=\{(x_1,\ldots,x_n) : x_i\in[k]\}$](img2.gif) .
.
Definition 5.1
A subset
![$ L\subseteq [k]^n$](img3.gif)
with
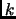
elements is called a
combinatorial line if we can arrange the elements in
an order so that in every coordinate either all the entries
are the same or they form the sequence
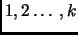
, in that order.
Note: A combinatorial line is a ``SET" in the game ``SET."
The converse is not true. (why?)
Theorem 5.2 (Hales-Jewett, 1963)
For all
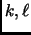
there exists an
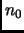
such that for all

and
any
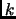
-coloring of
![$ [\ell]^n$](img9.gif)
, there exists a combinatorial line in one color.
Note: This theorem implies Van der Waerden's theorem:
Theorem 5.3 (Van der Waerden, 1927)
For any
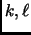
there exists

such that for all
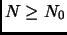
,
if we color
![$ [N]$](img12.gif)
with
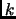
colors, then there is an

-term
arithmetic progression in one color.
The idea is to let
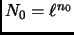 , and to associate with every number
in
, and to associate with every number
in ![$ [N]$](img12.gif) the digits in its expansion in the base-
the digits in its expansion in the base- number system.
Then any combinatorial line would correspond to an arithmetic progression.
(But not conversely. Why?)
number system.
Then any combinatorial line would correspond to an arithmetic progression.
(But not conversely. Why?)
Recall Szemerédi's Theorem, which is the ``density version'' of
van der Waerden's Theorem:
Theorem 5.4 (Szemerédi, 1975)
For all
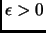
and

there exists

such that for all

, if
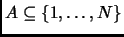
and

then
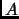
contains an

-term arithmetic progression.
The density version of the Hales-Jewett Theorem is:
Theorem 5.5 (Furstenberg-Katznelson)
For all
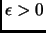
and all

there exists
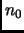
such that for
all

, if
![$ A\subseteq [\ell]^n$](img21.gif)
and
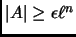
,
then
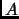
contains a combinatorial line.




Next: Hypergraphs
Up: Discrete Math, 5th day,
Previous: Discrete Math, 5th day,
Laszlo Babai
2004-06-27
![]() , and to associate with every number
in
, and to associate with every number
in ![]() the digits in its expansion in the base-
the digits in its expansion in the base-![]() number system.
Then any combinatorial line would correspond to an arithmetic progression.
(But not conversely. Why?)
number system.
Then any combinatorial line would correspond to an arithmetic progression.
(But not conversely. Why?)
