- (a)
- A hypergraph is a pair
 , where
, where 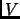 is
a set of vertices and
is
a set of vertices and  is a set of edges, an edge simply
being a subset of
is a set of edges, an edge simply
being a subset of 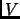 .
.
- (b)
- A hypergraph is called
 -uniform, if every edge has
-uniform, if every edge has  vertices.
vertices.
 .
.
Extremal set theory is concerned with problems of the following type:
determine (or estimate) the maximum number of edges of a hypergraph
satisfying certain conditions. We have seen some examples of this
already in graph theory, for instance the Mandel-Turán Theorem
and the Kovári-Sós-Turán Theorem. There are many more
that deal with hypergraphs. Ruzsa and Szemerédi, in examining the
combinatorial roots of Roth's Theorem on 3-term arithmetic progressions,
were lead to the following natural problem in extremal set theorey:
Question: What is the maximum number of edges of a ![]() -uniform
hypergraph satisfying the following two conditions:
-uniform
hypergraph satisfying the following two conditions:
Note that the maximum possible number of edges in a 3-uniform hypergraph
is
![]() , the total number of triples of vertices.
Condition (C1) already forces a lower (uadratic) rate of growth:
, the total number of triples of vertices.
Condition (C1) already forces a lower (uadratic) rate of growth:
![]()
Hint. For every pair of vertices there is at most one edge containing them; and every edge contains 3 pairs of vertices.
When we add condition C2, the rate of growth of the number of edges
drops even further, below quadratic:
We will see next time that this implies Roth's theorem (i.e.,
Szemerédi's theorem for ![]() ):
):
Roth's Theorem. Given
![]() there exists
there exists ![]() such that
for all
such that
for all ![]() , if
, if
![]() and
and
![]() , then
, then
![]() contains a 3-term arithmetic progression.
contains a 3-term arithmetic progression.
![]()