Because neither ![]() nor
nor
![]() ever fall to zero as
ever fall to zero as
![]() approaches infinity, the boundary spectrum
approaches infinity, the boundary spectrum
![]() will always have non-zero magnitude . Also, due to the
will always have non-zero magnitude . Also, due to the ![]() factor,
factor,
![]() is infinitely high near
is infinitely high near
![]() , and is
thus not integrable. Thus, it is not possible to discuss what
fraction of the boundary spectrum falls below the Nyquist frequency
for a given Gaussian attenuation. Rather, it only makes sense to
discuss the Nyquist criterion in relation to the Gaussian attenuation
itself. The relevant attribute of the Gaussian function is its width,
since this gives an indication of the range of frequencies which pass
through the measurement process. As the Gaussian function is always
positive, we must contrive some measure of its width. A common
engineering practice is to measure the ``Full Width Half Max''-- the
horizontal width of the function's graph at half of its maximum
height. For a Gaussian with standard deviation
, and is
thus not integrable. Thus, it is not possible to discuss what
fraction of the boundary spectrum falls below the Nyquist frequency
for a given Gaussian attenuation. Rather, it only makes sense to
discuss the Nyquist criterion in relation to the Gaussian attenuation
itself. The relevant attribute of the Gaussian function is its width,
since this gives an indication of the range of frequencies which pass
through the measurement process. As the Gaussian function is always
positive, we must contrive some measure of its width. A common
engineering practice is to measure the ``Full Width Half Max''-- the
horizontal width of the function's graph at half of its maximum
height. For a Gaussian with standard deviation ![]() , the the FWHM
is
, the the FWHM
is
![]() [KK68]. As the measurement attenuation Gaussian
has standard deviation
[KK68]. As the measurement attenuation Gaussian
has standard deviation ![]() , its FWHM is
, its FWHM is
![]() .
.
One plausible way relate the boundary thickness to the Nyquist rate is
to set the FWHM of the Gaussian function in frequency space to equal
the range of frequencies which satisfy the Nyquist criterion. If we
specify that the distance between data sample points is one unit (that
is, the length of a voxel's edge is one), then the Nyquist frequency
is ![]() radians per sample, and the range of frequencies which
satisfy the Nyquist criterion are from
radians per sample, and the range of frequencies which
satisfy the Nyquist criterion are from ![]() to
to ![]() . Then we have:
. Then we have:
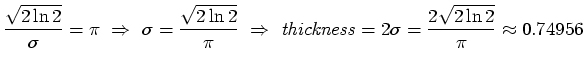 |
(33) |
It may seem that this boundary thickness will not be large enough to be detected by the histogram volume, if at any given location on the object surface only about one voxel can fit within the boundary region. However, we are helped by the fact that significant objects in a dataset tend to have large surface areas, and that the surfaces tend to take on a variety of orientations and positions relative to the sampling grid. To some extent this was illustrated with Figure 4.2 in the discussion of histogram volume formation.
At this point, however, we are also equipped to make a more
quantitative probabilistic argument. If an object measured in a
volume dataset has surface area ![]() , the boundary region surrounding
the object will have a volume approximately equal to
, the boundary region surrounding
the object will have a volume approximately equal to ![]() ,
since the boundary thickness is
,
since the boundary thickness is ![]() . Assuming that the dataset
sample points are distributed evenly throughout the volume inside the
boundary region, the amount of the boundary region volume gives the
approximate number of sample points within the boundary region. Thus,
if the Gaussian attenuation in frequency space has a standard deviation
. Assuming that the dataset
sample points are distributed evenly throughout the volume inside the
boundary region, the amount of the boundary region volume gives the
approximate number of sample points within the boundary region. Thus,
if the Gaussian attenuation in frequency space has a standard deviation
![]() , we can compute an approximate number of hits along the the
curves in the histogram volume:
, we can compute an approximate number of hits along the the
curves in the histogram volume:
| (34) |