


Next: Bandlimiting and thickness in
Up: Bandlimiting and the ``thickness''
Previous: Bandlimiting and the ``thickness''
Our goal here is to show the relationship between the boundary's
frequency content and its thickness, and how this relationship effects
our ability to record the presence of the boundary in the histogram
volume. The Fourier transform is an important part of this analysis,
and because there are variety of possible definitions for the
transform, we state the particular definitions being used here:
We will use the following to model the data value as a
function of position within a boundary region:
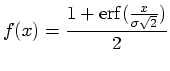 |
(24) |
Recall from Section 5.2 that the ``thickness'' of a
boundary is defined to be 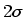 . Setting
. Setting
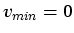 and
and
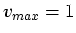 in the the formula for
in the the formula for 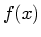 given in Section 5.1
produces Equation A.3. Any other values for the variables
given in Section 5.1
produces Equation A.3. Any other values for the variables
 and
and 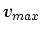 represent some scaling or shifting of the
boundary, and the Fourier transform is not meaningfully changed by
these operations.
represent some scaling or shifting of the
boundary, and the Fourier transform is not meaningfully changed by
these operations.
To find the Fourier transform of the 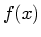 given above, we could
simply apply the definition of the Fourier transform to
given above, we could
simply apply the definition of the Fourier transform to 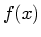 , and
then reduce the resulting expression. We can avoid this labor,
however, by exploiting a useful property of the transform under
integration, expressed here with
, and
then reduce the resulting expression. We can avoid this labor,
however, by exploiting a useful property of the transform under
integration, expressed here with
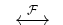 pointing to the two
expressions which are transforms of each other:
pointing to the two
expressions which are transforms of each other:
 |
(25) |
This states, in terms of a function 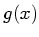 and its Fourier transform
and its Fourier transform
 , how to find the transform of an integral if we already know
the transform of the function being integrated. Aside from a ``DC''
term
, how to find the transform of an integral if we already know
the transform of the function being integrated. Aside from a ``DC''
term
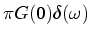 (which we will henceforth ignore18),
when we integrate a function, the corresponding transform is divided
by
(which we will henceforth ignore18),
when we integrate a function, the corresponding transform is divided
by 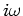 . We will use
Equation A.4 to find the transform of
. We will use
Equation A.4 to find the transform of 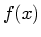 because
doing so will bring us directly in contact with the attenuation in
frequency space caused by the bandlimiting inherent in the
measurement.
because
doing so will bring us directly in contact with the attenuation in
frequency space caused by the bandlimiting inherent in the
measurement.
In order to exploit the property expressed in
Equation A.4, we find the derivative of 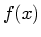 :
:
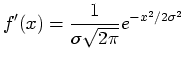 |
(26) |
By our choice of 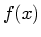 ,
, 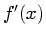 is a normalized Gaussian function
with standard deviation
is a normalized Gaussian function
with standard deviation 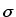 . Its Fourier transform is[KK68]:
. Its Fourier transform is[KK68]:
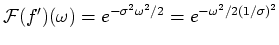 |
(27) |
Thus the transform of a Gaussian function is another Gaussian
function, and there is an exact reciprocal relationship between their
standard deviations. While the standard deviation in 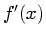 is
is 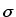 ,
in
,
in
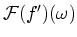 it is
it is 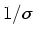 . Having
. Having 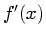 and its
transform
and its
transform
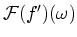 , we can now use
Equation A.4 to state the transform of the
measured boundary function:
, we can now use
Equation A.4 to state the transform of the
measured boundary function:
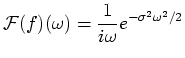 |
(28) |
It is possible to utilize the same process to find the transform
of the un-blurred boundary function, which represents the boundary prior
to the measurement process. This is the so-called Heaviside step
function 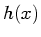 :
:
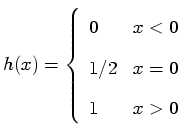 |
(29) |
By definition, the derivative of the step function is the delta
function
 . The Fourier transform of the
delta function is trivial to compute:
. The Fourier transform of the
delta function is trivial to compute:
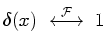 |
(30) |
Then by again using Equation A.4 we can find the
transform of the step function:
 |
(31) |
Since we know from Fourier theory that the spectrum of the convolution
of two functions is exactly the product of the two functions' spectra,
we see from the expression for
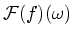 (Equation A.7) that the spectrum of the measured boundary
is the product of the spectrum of the step function (
(Equation A.7) that the spectrum of the measured boundary
is the product of the spectrum of the step function (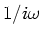 ) times a
Gaussian function
) times a
Gaussian function
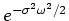 . Thus,
. Thus,
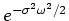 is
precisely the attenuation in frequency caused by the bandlimiting in
the measurement process. We can now state the relationship between
measured boundary thickness and bandlimiting:
is
precisely the attenuation in frequency caused by the bandlimiting in
the measurement process. We can now state the relationship between
measured boundary thickness and bandlimiting:
The boundary thickness will be 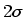 when the bandlimiting due to
measurement is equivalent to multiplication in frequency space by a
Gaussian function with standard deviation
when the bandlimiting due to
measurement is equivalent to multiplication in frequency space by a
Gaussian function with standard deviation 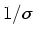 .
.
Footnotes
- ... ignore18
- The
DC (direct current) component of the Fourier transform represents the
average value of the function. Since all the relevant characteristics
of the boundary's Fourier transform are in terms of non-zero
frequencies, the DC component is not important for this analysis.



Next: Bandlimiting and thickness in
Up: Bandlimiting and the ``thickness''
Previous: Bandlimiting and the ``thickness''
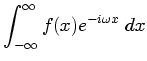
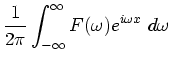
![]() given above, we could
simply apply the definition of the Fourier transform to
given above, we could
simply apply the definition of the Fourier transform to ![]() , and
then reduce the resulting expression. We can avoid this labor,
however, by exploiting a useful property of the transform under
integration, expressed here with
, and
then reduce the resulting expression. We can avoid this labor,
however, by exploiting a useful property of the transform under
integration, expressed here with
![]() pointing to the two
expressions which are transforms of each other:
pointing to the two
expressions which are transforms of each other:
![]() :
:
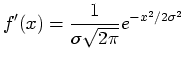
![]() :
:
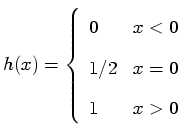
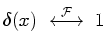

when the bandlimiting due to measurement is equivalent to multiplication in frequency space by a Gaussian function with standard deviation
.