


Next: Opacity functions of data
Up: Opacity function generation
Previous: Opacity function generation
Mathematical boundary analysis
In order to develop a method for opacity function generation that uses
our boundary model and the information stored in the histogram volume,
we need to look at the equation used to describe the ideal
boundary data value as a function of position, as plotted in
Figure 3.4:
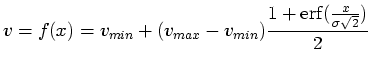 |
(6) |
In its current form, the ideal boundary gets its characteristic shape
from the
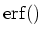 function. We define this important function and
plot it in Figure 5.1.
function. We define this important function and
plot it in Figure 5.1.
 |
(7) |
Figure 5.1:
The error function,
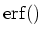
![\begin{figure}
\centering {
\psfrag{erfx}[bc]{\raisebox{8pt}{$y = \operatorname...
...pace{4pt}$x$}
\epsfig {figure=eps/erf.eps, width=0.5\columnwidth}}
\end{figure}](img83.gif) |
Note in Figure 5.1 that since
 is centered
around the origin, the boundary function
is centered
around the origin, the boundary function 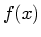 is also centered
around where position
is also centered
around where position 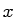 is zero. There are two essential
differences between
is zero. There are two essential
differences between 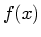 and
and
 . First, in
. First, in 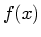 the
argument of
the
argument of
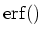 is scaled by
is scaled by
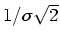 . The
. The  parameter
controls the thickness, or spread, of the boundary. For large
parameter
controls the thickness, or spread, of the boundary. For large  ,
the argument of
,
the argument of
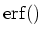 is reduced, and the boundary is stretched out
more. The boundary is much narrower and sharper with a small
is reduced, and the boundary is stretched out
more. The boundary is much narrower and sharper with a small 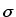 .
Second,
.
Second,
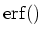 's range has been shifted and scaled so that the range
of
's range has been shifted and scaled so that the range
of 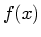 is between
is between  and
and 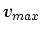 . As
. As 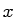 approaches
negative infinity,
approaches
negative infinity,
 approaches
approaches 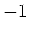 , and
thus
, and
thus 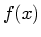 approaches
approaches  . Conversely, as
. Conversely, as 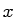 approaches
positive infinity,
approaches
positive infinity, 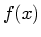 approaches
approaches 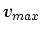 . At
. At 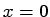 , the middle
of the boundary,
, the middle
of the boundary, 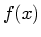 is half-way between
is half-way between  and
and 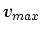 .
.
The first and second derivatives of  are as follows:
are as follows:
Our choice of boundary parameterization means that 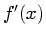 is a
normalized Gaussian, with
is a
normalized Gaussian, with 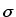 being the usual standard deviation.
being the usual standard deviation.
Figure 5.2:
Relationship between thickness and the boundary function. The
thickness of material boundaries is defined to be 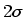 , which extends
from one extremum in
, which extends
from one extremum in 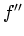 to the other. The middle of the boundary
is defined to be where
to the other. The middle of the boundary
is defined to be where 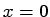 .
.
 |
Since the Gaussian has inflection points at 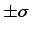 , this is where
, this is where
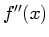 attains its extrema. The same positions can serve as
(somewhat artificial) delimiters for the extent of the boundary. We
define the ``thickness'' of the boundary to be
attains its extrema. The same positions can serve as
(somewhat artificial) delimiters for the extent of the boundary. We
define the ``thickness'' of the boundary to be 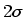 .
Figure 5.2 shows how the the definition of thickness
roughly accounts for the region in which the data value transitions
between the values on either side of the boundary.
.
Figure 5.2 shows how the the definition of thickness
roughly accounts for the region in which the data value transitions
between the values on either side of the boundary.
The equations for 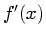 (Equation 5.3) and
(Equation 5.3) and 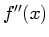 (Equation 5.4) look very similar because of the special
derivative properties of
(Equation 5.4) look very similar because of the special
derivative properties of 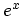 . In fact, the only difference between
. In fact, the only difference between
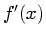 and
and 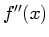 is a scaling factor
is a scaling factor
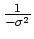 and the
position
and the
position 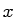 :
:
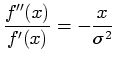 |
(10) |
This is intriguing because it means there is a way to infer the position
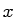 along a boundary knowing just
along a boundary knowing just 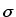 and the first and second
derivatives.
and the first and second
derivatives. 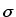 can be recovered if the extremal values of
can be recovered if the extremal values of 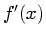 and
and
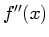 are known. Recall from Figure 5.2 that
are known. Recall from Figure 5.2 that
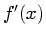 has its maximum at 0, and that
has its maximum at 0, and that 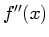 has a maximum at
has a maximum at 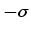 and a minimum at
and a minimum at 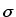 . This gives us two different ways of calculating
. This gives us two different ways of calculating 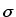 .
.
Knowing 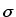 , one can then recover position from
, one can then recover position from 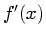 and
and 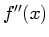 with
Equation 5.5:
with
Equation 5.5:
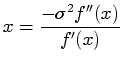 |
(12) |
Section 3.4 described the ability to transform
the first and second derivatives as functions of position into
functions of data value. That transformation takes on special
importance in light of Equation 5.7. 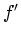 and
and 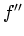 are
functions of position in that equation, but there is no reason why
they couldn't also be functions of data value. In that case, we would
have a way to map from data value back to position along a boundary.
Since our goal is to produce an opacity function which makes the
middle of boundaries opaque, this information is exactly what is
necessary for opacity function generation.
are
functions of position in that equation, but there is no reason why
they couldn't also be functions of data value. In that case, we would
have a way to map from data value back to position along a boundary.
Since our goal is to produce an opacity function which makes the
middle of boundaries opaque, this information is exactly what is
necessary for opacity function generation.
Fortunately, the histogram volume contains that information. The
histogram volume was created by recording the position-independent
relationship between the data value and its derivatives. In that
case, the position that was ``projected out'' in the histogram
formation was the 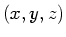 position within the volume. Now, having
created the histogram volume, in the next section we will analyze it
in order to re-create ``position'' information with
Equation 5.7. This time, the ``position'' in question is
actually a signed distance to the nearest boundary, which will be
extremely helpful in the creation of opacity functions.
position within the volume. Now, having
created the histogram volume, in the next section we will analyze it
in order to re-create ``position'' information with
Equation 5.7. This time, the ``position'' in question is
actually a signed distance to the nearest boundary, which will be
extremely helpful in the creation of opacity functions.



Next: Opacity functions of data
Up: Opacity function generation
Previous: Opacity function generation
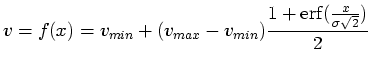

![]() are as follows:
are as follows:

![]() (Equation 5.3) and
(Equation 5.3) and ![]() (Equation 5.4) look very similar because of the special
derivative properties of
(Equation 5.4) look very similar because of the special
derivative properties of ![]() . In fact, the only difference between
. In fact, the only difference between
![]() and
and ![]() is a scaling factor
is a scaling factor
![]() and the
position
and the
position ![]() :
:
![]() and
and ![]() are
functions of position in that equation, but there is no reason why
they couldn't also be functions of data value. In that case, we would
have a way to map from data value back to position along a boundary.
Since our goal is to produce an opacity function which makes the
middle of boundaries opaque, this information is exactly what is
necessary for opacity function generation.
are
functions of position in that equation, but there is no reason why
they couldn't also be functions of data value. In that case, we would
have a way to map from data value back to position along a boundary.
Since our goal is to produce an opacity function which makes the
middle of boundaries opaque, this information is exactly what is
necessary for opacity function generation.
![]() position within the volume. Now, having
created the histogram volume, in the next section we will analyze it
in order to re-create ``position'' information with
Equation 5.7. This time, the ``position'' in question is
actually a signed distance to the nearest boundary, which will be
extremely helpful in the creation of opacity functions.
position within the volume. Now, having
created the histogram volume, in the next section we will analyze it
in order to re-create ``position'' information with
Equation 5.7. This time, the ``position'' in question is
actually a signed distance to the nearest boundary, which will be
extremely helpful in the creation of opacity functions.