


Next: The transformation from position
Up: Mathematical foundations
Previous: Directional derivatives along the
Studying  ,
, 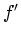 , and
, and 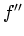 in a boundary
in a boundary
Even though the first and second directional derivatives are
quantities defined in three dimensions, the significant relationship
between them can be reduced to a one dimensional case,
because we only care about the value and its derivatives as we move
along the gradient direction. Thus, in analyzing the relationship
between  ,
, 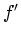 , and
, and 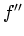 , it suffices to study a one dimensional
sampling perpendicular to the surface. Figure 3.4
, it suffices to study a one dimensional
sampling perpendicular to the surface. Figure 3.4
Figure 3.4:
Ideal boundary analysis. The
data value and its first and second derivatives are sampled along
a short segment which passes through an object boundary
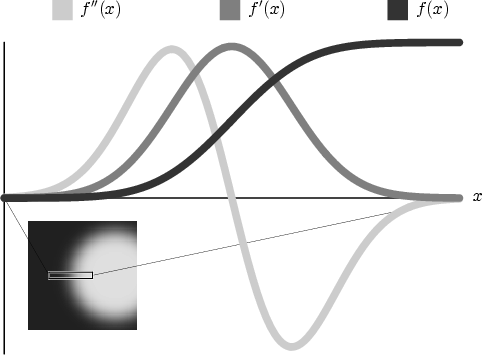 |
analyzes one segment of a slice from the synthetic cylinder dataset.
Shown are plots of the data value, and the first and second
derivatives, as we move across the cylinder's boundary. The direction
of the gradient obviously varies throughout the volume, but the
observed relationship between  and its directional derivatives is
constant, because the boundary is assumed uniform everywhere. Note
that at the mid-point of the boundary, the first derivative is at a
maximum, and the second derivative has a zero-crossing. Because of
blurring, the boundary is spread over a range of positions, but the
maximum in
and its directional derivatives is
constant, because the boundary is assumed uniform everywhere. Note
that at the mid-point of the boundary, the first derivative is at a
maximum, and the second derivative has a zero-crossing. Because of
blurring, the boundary is spread over a range of positions, but the
maximum in 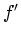 and/or the zero-crossing in
and/or the zero-crossing in 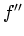 provides a way to
define an exact spatial location of a boundary. Indeed, two edge
detectors common in computer vision, Canny
[Can86] and Marr-Hildreth [MH80], use the
provides a way to
define an exact spatial location of a boundary. Indeed, two edge
detectors common in computer vision, Canny
[Can86] and Marr-Hildreth [MH80], use the 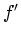 and
and 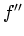 criteria, respectively, to find edges.
criteria, respectively, to find edges.



Next: The transformation from position
Up: Mathematical foundations
Previous: Directional derivatives along the
![]() ,
, ![]() , and
, and ![]() , it suffices to study a one dimensional
sampling perpendicular to the surface. Figure 3.4
, it suffices to study a one dimensional
sampling perpendicular to the surface. Figure 3.4
