


Next: Studying , , and
Up: Mathematical foundations
Previous: Boundary model
Directional derivatives along the gradient
Although it was suggested in Section 1.2 that
isosurfaces are not always sufficient for visualizing objects in real
world volume data, the method presented in this thesis still
indirectly employs them as an indicator of object shape.
Figure 3.2:
Isosurfaces tend to conform to object shape. For a cylindrical
object (a) with a soft boundary, a small patch of an isosurface
(b) is shown within the boundary, together with a line segment
(c) which follows the gradient direction, perpendicular to the
isosurface patch and to the object boundary.
![\begin{figure}
\psfrag{a}[l]{\hspace{3pt}(a)}
\psfrag{b}[l]{\hspace{3pt}(b)}
...
...ng {
\epsfig {figure=eps/isofrag.high.eps, width=0.5\textwidth} }
\end{figure}](img33.gif) |
That is, based on the mathematical property that the gradient vector
at some position always points perpendicular to an isosurface through
that position, we use the gradient vector as a way of finding the
direction which passes perpendicularly through the object boundary.
Figure 3.2 demonstrates, for a simple cylindrical object
with a soft boundary, how a line segment along the gradient direction
lies perpendicular to a patch of the boundary isosurface, and how the
isosurface patch conforms to the shape of the boundary. However, in
real datasets, the isosurfaces don't always perfectly conform to the
local shape of the underlying object. But on average, over the
whole volume, the gradient vector does tend to point perpendicular to
the object boundary. Therefore, our approach will be to rely on the
statistical properties of the histogram to provide the overall picture
of the boundary characteristics throughout the entire volume.
The directional derivative of a scalar field  along a vector
along a vector
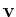 , denoted
, denoted
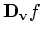 , is the derivative of
, is the derivative of
 as one moves along a straight path in the
as one moves along a straight path in the
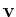 direction.
This thesis studies
direction.
This thesis studies  and its derivatives along a path which is
normal to the object boundary -- moving along the gradient direction
-- in order to create an opacity function. Because the direction
along which we're computing the directional derivative is always
that of the gradient, we employ a mild abuse of notation, using
and its derivatives along a path which is
normal to the object boundary -- moving along the gradient direction
-- in order to create an opacity function. Because the direction
along which we're computing the directional derivative is always
that of the gradient, we employ a mild abuse of notation, using 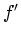 and
and 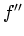 to signify the first and second directional derivative along
the gradient direction, even though these would be more properly
denoted by
to signify the first and second directional derivative along
the gradient direction, even though these would be more properly
denoted by
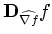 and
and
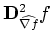 , where
, where
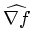 is
the gradient direction. We treat
is
the gradient direction. We treat  as if it were a function of
just one variable, keeping in mind that the axis along which we
analyze
as if it were a function of
just one variable, keeping in mind that the axis along which we
analyze  always follows
always follows
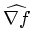 , which constantly
changes orientation depending on position.
Figure 3.3 shows how the gradient direction changes
with position to stay normal to the isosurfaces of a simple object.
, which constantly
changes orientation depending on position.
Figure 3.3 shows how the gradient direction changes
with position to stay normal to the isosurfaces of a simple object.
Figure 3.3:
The gradient direction 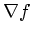 (c) changes with position in
the data (a), but it maintains its perpendicular orientation
with respect to the isosurfaces (b).
(c) changes with position in
the data (a), but it maintains its perpendicular orientation
with respect to the isosurfaces (b).
![\begin{figure}\setcounter {subfigure}{0}\setlength {\figsz}{0.30\columnwidth}\...
...$]{
\epsfig {figure=eps/graddemo-vecs.eps,
width=\figsz}}
}
}
\end{figure}](img39.gif) |



Next: Studying , , and
Up: Mathematical foundations
Previous: Boundary model
![\begin{figure}
\psfrag{a}[l]{\hspace{3pt}(a)}
\psfrag{b}[l]{\hspace{3pt}(b)}
...
...ng {
\epsfig {figure=eps/isofrag.high.eps, width=0.5\textwidth} }
\end{figure}](img33.gif)
![\begin{figure}
\psfrag{a}[l]{\hspace{3pt}(a)}
\psfrag{b}[l]{\hspace{3pt}(b)}
...
...ng {
\epsfig {figure=eps/isofrag.high.eps, width=0.5\textwidth} }
\end{figure}](img33.gif)
![]() along a vector
along a vector
![]() , denoted
, denoted
![]() , is the derivative of
, is the derivative of
![]() as one moves along a straight path in the
as one moves along a straight path in the
![]() direction.
This thesis studies
direction.
This thesis studies ![]() and its derivatives along a path which is
normal to the object boundary -- moving along the gradient direction
-- in order to create an opacity function. Because the direction
along which we're computing the directional derivative is always
that of the gradient, we employ a mild abuse of notation, using
and its derivatives along a path which is
normal to the object boundary -- moving along the gradient direction
-- in order to create an opacity function. Because the direction
along which we're computing the directional derivative is always
that of the gradient, we employ a mild abuse of notation, using ![]() and
and ![]() to signify the first and second directional derivative along
the gradient direction, even though these would be more properly
denoted by
to signify the first and second directional derivative along
the gradient direction, even though these would be more properly
denoted by
![]() and
and
![]() , where
, where
![]() is
the gradient direction. We treat
is
the gradient direction. We treat ![]() as if it were a function of
just one variable, keeping in mind that the axis along which we
analyze
as if it were a function of
just one variable, keeping in mind that the axis along which we
analyze ![]() always follows
always follows
![]() , which constantly
changes orientation depending on position.
Figure 3.3 shows how the gradient direction changes
with position to stay normal to the isosurfaces of a simple object.
, which constantly
changes orientation depending on position.
Figure 3.3 shows how the gradient direction changes
with position to stay normal to the isosurfaces of a simple object.
![\begin{figure}\setcounter {subfigure}{0}\setlength {\figsz}{0.30\columnwidth}\...
...$]{
\epsfig {figure=eps/graddemo-vecs.eps,
width=\figsz}}
}
}
\end{figure}](img39.gif)