


Next: Directional derivatives along the
Up: Mathematical foundations
Previous: Mathematical foundations
Boundary model
The methods presented in this thesis make the task of volume rendering
surfaces more intuitive and less labor intensive than previous
methods. The algorithm is based on the computation of boundary
characteristics in a volume and using this information to guide the
user towards opacity function settings which readily display the
boundaries. Towards that end, a mathematical model has been chosen
for what constitutes an ideal boundary. We now describe the boundary
model upon which the techniques of this thesis are based.
We assume that at their boundary, objects have a sharp, discontinuous
change in the physical property measured by the values in the dataset.
In MRI this property might be density of hydrogen nuclei, in CT and EM
it is radio-opacity of the tissue. Also, we assume that the data is
band-limited prior to sampling, but not with the usual Nyquist
criterion. Rather, the measurement process is assumed to have a
Gaussian frequency response, which effectively blurs the sharp edges
with a Gaussian filter.
Figure 3.1:
The ideal physical boundary (a) is convolved with a Gaussian
filter (b) representing the frequency response of the measurement
process, producing the measured boundary prior to sampling (c)
which exhibits the shape of the
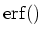 function.
function.
![\begin{figure}\setcounter {subfigure}{0} \centering {
\mbox{
\subfigure[]{ \...
...]{ \epsfig {file=eps/idealberf.eps, width=0.27\columnwidth}}
}
}
\end{figure}](img32.gif) |
Figure 3.1 shows a step function representing an ideal
boundary prior to measurement, the Gaussian filter which performs the
band-limiting by blurring, and the resulting measured boundary (prior
to sampling). The resulting curve (Figure 3.1(c))
happens to be the integral of the Gaussian kernel, which is called the
error function, notated ``
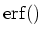 ''[KK68].
Actual measurement devices necessarily band-limit, so they always blur
boundaries somewhat. Their frequency response is never exactly a
Gaussian function, however, since this requires infinite support, and
infinitely high frequencies cannot be measured. Although certain
mathematical properties of the Gaussian function are exploited later,
the inexact match of real-world sampling to the Gaussian ideal has not
been found to severely limit application of the techniques presented here. A
final assumption made for the purposes of this analysis is that the
blurring is isotropic, that is, uniform in all directions. Again, the
algorithms presented in this thesis will often work even if a given
dataset doesn't have this characteristic, but results may be improved
if it is pre-processed to approximate isotropic blurring. Having
previously assumed that objects are made of material which attains the
same data value everywhere in their interior, this is effectively
equivalent to assuming that the boundaries of objects will be uniform
over their entire surface. The consequences of these various
assumptions will be evident when histogram volume calculation is
discussed in Chapter 4.
''[KK68].
Actual measurement devices necessarily band-limit, so they always blur
boundaries somewhat. Their frequency response is never exactly a
Gaussian function, however, since this requires infinite support, and
infinitely high frequencies cannot be measured. Although certain
mathematical properties of the Gaussian function are exploited later,
the inexact match of real-world sampling to the Gaussian ideal has not
been found to severely limit application of the techniques presented here. A
final assumption made for the purposes of this analysis is that the
blurring is isotropic, that is, uniform in all directions. Again, the
algorithms presented in this thesis will often work even if a given
dataset doesn't have this characteristic, but results may be improved
if it is pre-processed to approximate isotropic blurring. Having
previously assumed that objects are made of material which attains the
same data value everywhere in their interior, this is effectively
equivalent to assuming that the boundaries of objects will be uniform
over their entire surface. The consequences of these various
assumptions will be evident when histogram volume calculation is
discussed in Chapter 4.



Next: Directional derivatives along the
Up: Mathematical foundations
Previous: Mathematical foundations
![\begin{figure}\setcounter {subfigure}{0} \centering {
\mbox{
\subfigure[]{ \...
...]{ \epsfig {file=eps/idealberf.eps, width=0.27\columnwidth}}
}
}
\end{figure}](img32.gif)
![\begin{figure}\setcounter {subfigure}{0} \centering {
\mbox{
\subfigure[]{ \...
...]{ \epsfig {file=eps/idealberf.eps, width=0.27\columnwidth}}
}
}
\end{figure}](img32.gif)