Homework, material covered

Class 18, Tue 12-03  
Inclusion-Exclusion. The Derangement problem. Independence of random variables. Planar graphs: Kuratowski's Theorem.
Problems due Thursday, Dec 5: 17.1, 17.3, 17.4B, 17/7B, 17.14B, 17.38, 17.39, 17.43B, 17.44B

18.1 DO (DeMorgan's Identities) Let $A_1,\dots,A_k\subseteq\Omega$. Then $$ \overline{\bigcup_{i=1}^k A_i} = \bigcap_{i=1}^k \Abar_i $$ and $$ \overline{\bigcap_{i=1}^k A_i} = \bigcup_{i=1}^k \Abar_i $$

18.2 Inclusion-Exclusion Principle. Let $A_1,\dots,A_k\subseteq\Omega$ be events and let $B$ denote the complement of their union. Then $$P(B) = S_0 - S_1 + S_2 - + \dots + (-1)^k S_k$$ where $S_t$ denotes the sum of the probabilities of the $t$-wise intersections of the $A_i$. ($S_0=1$.) For instance, for $k=3$ the formula takes the form $$P(B)= S_0 - S_1 + S_2 - S_3 = 1-\left(P(A_1)+P(A_2)+P(A_3)\right)+ \left(P(A_1\cap A_2)+P(A_1\cap A_3)+P(A_2\cap A_3)\right) - P(A_1\cap A_2\cap A_3) $$

The number of terms in the definition of $S_t$ is $\binom{n}{t}$.

18.3 REVIEW the proof via indicator variables.

18.4 DO   Bonferroni's inequalities (truncated Inclusion-Exclusion)

18.5 Derangement problem (also called the "Hat-checker problem")   Determine the probability $p_n$ that a random permutation of the set $[n]$ is fixed-point-free.   The answer is $$ p_n = \sum_{k=0}^n \frac{(-1)^k}{k!} $$ 18.6 DO   Prove this formula. Use Inclusion-Exclusion.

18.7 DO   Prove:   $p_n \to 1/\eee$.   In fact, this is a rapid convergence:   $|p_n - 1/\eee| < 1/(n+1)!$

18.10 REVIEW the concept of independence of random variables (see FPS).

18.11 DO   Every sublist of a list of independent random variables is independent.

18.12 DO   A list of indicator variables is independent if and only if the corresponding events are independent.

18.13 DO   If $X_1,\dots,X_k$ are independent random variables then   $E\left(\prod X_i\right) = \prod E(X_i)\,$.

18.15 DEF   A Kuratowski graph is a topological $K_5$ or a topological $K_{3,3}$.

18.16 Kuratowski's Theorem   A graph is planar if and only if it does not contain a Kuratowski subgraph.

18.17 REVIEW the concept of "good characterization" (Edmonds, 1968)

18.18 DO   Find a graph that is not planar and has no cycle shorter than $100$.

18.19 DO   (a) Find a Kuratowski subgraph of the Petersen graph.   (b) Show that Petersen's graph does not contain a topological $K_5$.

18.20 DO   Prove: If a connected graph $G$ has $m\le n+2$ edges then $G$ is planar.

Class 17, Tue 11-26  
Calculus review. Extremal graph theory. The probabilistic method. Planar graphs. Collisions, hash functions. Universal families of hash functions. Birthday paradox.

17.1 HW (4 points, dur Thu, Dec 5) Let $a_n, b_n > 0$ and $a_n\to\infty$. Prove: if $a_n=\Theta(b_n)$ then $\ln a_n \sim \ln b_n$.

17.2 REVIEW FROM CALCULUS   For all $x\in\rrr$, $$ \lim_{n\to\infty} \left(1+\frac{x}{n}\right)^n = \eee^x $$ In particular, $(1 + 1/n)^n \to \eee$ and $(1-1/n)^n \to 1/\eee$.

17.3 HW (4 points, due Thu, Dec 5)   Find a sequence $a_n$ such that $a_n\to 1$ but $(a_n)^n \to\infty$. Define your sequence in a way as to make these statements about your sequence as easy to prove as possible. No proof required.

17.4 HW (4 points, due Thu, Dec 5)   Prove: $\eee^x-1\sim x$ as $x\to 0$.

17.5 Bonus (4 points, due Thu, Dec 5)   Prove:    $\displaystyle{n^{1/n}-1 \sim \frac{\ln n}{n}} \,.$

17.6 HW (4 points)   For every $n$ find a triangle-free graph $G$ with $\Omega(n^2)$ edges. Make the ratio $m/n^2$ converge to a constant $c >0$. Make $c$ as large as possible; state its value. No proof required.   WARNING. Typo in this problem fixed 12-1 at 4:30pm. The typo was "$m/n$" instead of the intended "$m/n^2$".

17.7 Bonus (8 points, due Thursday, Dec 5)   Let $G$ be a $C_4$-free graph (no 4-cycles). Prove:   $m = O(n^{3/2})$.   Hint. Count the paths of length 2 in $G$ in two ways.

17.8 THEOREM. Every graph $G$ with $m$ edges has a bipartite subgraph with $\ge m/2$ edges.

17.9a HW (7 points) Give a probabilistic proof of Theorem 17.8 as follows. Color each vertex of $G$ red/blue at random (flipping a fair coin). What is the expected number of red-blue edges?

17.9b Remark. Note that the proof outlined in Exercise 17.9a shows the existence of an object without constructing the object. This is the essence of the probabilistic method championed especially by Paul Erdös (1913-1996).

17.9c DO   Give an algorithmic proof of Theorem 17.8.

17.10a DEF   A Hamilton cycle in a graph is a cycle of length $n$ (it passes through all vertices). The graph is Hamiltonian if is it has a Hamilton cycle.

17.10b DO   Prove that the dodecahedron is Hamiltonian.

17.10c DO   Prove that the Petersen graph is NOT Hamiltonian.   -- No elegant proof is known. You can greatly cut down on the number of cases by proving that all paths of length 3 are equivalent under automorphisms (self-isomorphisms).

17.11 HW (5 points) Prove: If $k\ell$ is odd then $\grid(k,\ell)$ is not Hamiltonian. (One-line proof.)

17.12 Greedy graph coloring algorithm
Let $G$ be a graph with $V(G)=[n]$. "Colors" are integers $\ge 1$.

    for $i=1$ to $n$
          assign the least available color to $i$
    end(for)
"Available color" for vertex $i$ means a color that has not been used to color any neighbor $j$ of $i$ ($j < i$).

17.13 DO (Greedy coloring is good)  Show that the greedy coloring algorithm will use at most $1+\max\deg$ colors, where $\max\deg$ denotes the maximum degree of the vertices of $G$.

17.14 Bonus (greedy coloring is bad) (6 points, due Thursday, Dec 5) For every even value $n$ find a bipartite graph $G$ with $n$ vertices such that the greedy graph coloring algorithm uses $n/2$ colors.

17.15 DEF   A plane drawing of a graph is a representation of the vertices by points in the plane and the edges by arcs (continuous curves) without unwanted intersections (i.e., the only point of intersection of two arcs should be their shared endpoint). A graph is planar if if has a plane drawing.

17.16a DO   If $G$ is planar and $H\subseteq G$ then $H$ is planar.

17.16b DO   Show that all trees are planar.

17.17 DO   (a) Show that $K_4$ is planar. (b) Show that $K_5-e$ is planar for any $e\in E(K_5)$. (c) Show that $K_{2,3}$ is planar. (d) Show that $K_{3,3}-e$ is planar for any $e\in E(K_{3,3})$.

17.18 THEOREM   (a) If $G$ is a planar graph and $n\ge 3$ then $m\le 3n-6$.   (b) If $G$ is a triangle-free planar graph and $n\ge 3$ then $m\le 2n-4$.

17.19 Bonus (5+6 points) (a) Prove that the inequality $m\le 3n-6$ in 17.18 (a) is tight for all $n\ge 3$, i.e., $(\forall n\ge 3)$ there exists a planar graph with $m=3n-6$ edges.   (b) Prove that the inequality $m\le 2n-4$ in 17.18 (b) is tight for all $n\ge 3$, i.e., $(\forall n\ge 3)$ there exists a triangle-free planar graph with $m=2n-4$ edges.

17.20 HW (2+2 points)   Use Theorem 17.18 to prove that $K_5$ and $K_{3,3}$ are not planar.

17.21 HW (4 points)   Use Theorem 17.18 to prove that every planar graph has a vertex of degree $\le 5$.

17.22 HW (7 points) Use 17.21 to prove that every planar graph is 6-colorable.

17.23 STUDY the history of the 4-COLOR THEOREM: Every planar graph is 4-colorable.

17.24 DEF   Consider a function $f : A\to B$. Let $x,y\in A$, $x\neq y$. We say that $x$ and $y$ collide under $f$ if $f(x)=f(y)$. The number of collisions of $f$, $\coll(f)$, is the number of those pairs $\{x,y\}$ that collide.

17.25 DO   Let $A, B$ be non-empty sets, $|A|=n$, $|B|=k$. Let $f:A\to B$ be a function. (a)   $0\le \coll(f)\le \binom{n}{2}$.   (b)   $\coll(f)= \binom{n}{2}$ if and only if $f$ is a constant function, i.e., $|\range(f)|=1$.

17.26 Bonus (8 points)   Let $A, B$ be non-empty sets, $|A|=n$, $|B|=k$. Let $f : A\to B$ be a function. Prove: $$ \coll(f) \ge \frac{n(n-k)}{2k}\,.$$ Make your proof short and elegant. Show all your work!

17.27 DEF (Universal families of hash functions)   Let $\calF=(f_1,\dots,f_m)$ be a list of functions $f_i:A\to B$. We say that $\calF$ is a universal family of $A\to B$ hash functions if for all $x,y\in A$, if $x\neq y$ then $$ P_{i\in [m]} (f_i(x)=f_i(y)) \le \frac{1}{|B|} $$ where the probability is with respect to the uniform distrbution over $[m]$. (The sample space is $[m]$.)   Note that the $f_i$ do not need to be distinct in this definition.
This concept was introduced by Larry Carter and Mark Wegman in 1979.

17.28 HW (6 points) Let $A$, $B$ be non-empty sets. Recall that $B^A$ denotes the set of all functions $f:A\to B$. Prove:   $B^A$ is a universal family of $A\to B$ hash functions.

17.29 HW (5 points) Let $A$, $B$ be non-empty sets, $|A|=n$, $|B|=k$. Let $\calF=(f_1,\dots,f_m)$ be a universal family of $A\to B$ hash functions. Prove:   $$ E_{i\in [m]}(\coll(f_i)) \le \frac{n(n-1)}{2k} $$

17.30 DO   Compare the right-hand sides of the equations in problems 17.26 and 17.29. Observe that universal families of hash functions are asymptotically optimal in the following sense. Assume $k=o(n)$ as $n\to\infty$. Then $$ \frac{n(n-k)}{2k} \sim \frac{n(n-1)}{2k} $$ so the expected number of collisions of $f\in\calF$ is asymptotically not worse than the minimum possible number of collisions.

17.31 DO   Let $U$, $B$ be non-empty sets and let $\calF=(f_1,\dots,f_m)$ be a universal family of $U\to B$ hash functions. Let $A\subseteq U$ be a non-empty subset and let $g_i$ denote the restriction of $f_i$ to $A$. (So the domain of $g_i$ is $A$, and for $x\in S$ we set $g_i(x) := f_i(x)$.) Then $(g_1,\dots,g_m)$ is a universal family of $A\to B$ hash functions.

17.32 MOTIVATION   The significance of the preceding exercise is that our data set $A$ tends to be an unpredictable and dynamically changing subset of a fixed, much larger set $U$ which we call the "universe." For instance, $A$ could consist of identifying information of each employee of a large organization. Each record could include the name, date and place of birth, mother's maiden name, etc. -- an alphanumerical string of possibly 30 or more characters. The universe would be the set of all strings of the given length, so it could have size $34^{30}$ while we might have $|A|=10^5$. We need to create unique short codes for the employees. We could select a codomain $B$ of size $|B|\approx |A|$ and try to use a hash function $h: U\to B$, hoping that $h$ restricted to $A$ would have few collisions. This will not work with a single function $h$ but random selection from a universal family $\calF$ of $U\to B$ hash functions will achieve the goal. Additionally we need that each function in $\calF$ have a short description that permits the function to be easily computed. So the set $\calF=B^U$ is out of the question; the description length of most functions in $B^U$ is at least $\log |B^U|= |U|\log |B|\ge|U|$. Instead, we shall see that we can make the description length logarithmic in $|U|$, using a little number theory (matrices modulo $p$).

17.33 MATRICES mod $p$   Let $p$ be a prime number. Let $\zzz_p$ denote the set of residue classes mod $p$. Let $\zzz_p^{r\times s}$ denote the set of $r\times s$ matrices over $\zzz_p$.

17.34 DO   Prove:   $|\zzz^{r\times s}| = p^{rs}$.

17.35 LINEAR MAPS mod $p$   For $\zzz^{r\times 1}$ we simply write $\zzz_p^s$ and call the elements of this set column vectors of dimension $r$. Let $M\in \zzz_p^{r\times s}$ and $x\in \zzz_p^s$. Then the matrix product $Mx$ is defined (review matrix multiplication) and $Mx\in \zzz_p^r$. We call the function $x\mapsto Mx$ a linear function over $\zzz_p$ and we write $M : \zzz_p^s \to \zzz_p^r$.

17.36 Bonus (Linear maps as hash functions, 7 points)   Let $U =\zzz_p^m$ and $B=\zzz_p^{\ell}$. Let $\calF=\zzz^{\ell\times m}$. Prove that $\calF$ is a universal family of $U\to B$ hash functions.

17.37 REMARK   In this example, we have $|U|=p^m$ while the description length of each function in the family $\calF$ is $m\ell\log p=m\log |B|$. This is linear in $m$ (as opposed to exponential, as in $p^m$). The members of this family are efficiently computable (by matrix multiplication).

17.38 HW (7+2 points, due Thu, Dec 5) Let $B$ be a random $k$-subset of $[n]$ (so $|B|=k$) and let $C$ be a random $\ell$-subset of $[n]$.   (a) Determine $E(|B\cap C|)$. Your answer should be a very simple closed-form expression in terms of $k,\ell$, and $n$.   (b) What is the size of the sample space for this experiment?

17.39 HW (due Thu, Dec 5, 5 points) Let $0 \le a_i \le 1$. Prove:   $\prod_{i=1}^k (1-a_i) \ge 1 - \sum_{i=1}^k a_i\,.$

17.40 DO   Prove:   $(\forall x\in\rrr)(\eee^x \ge 1+x)$

17.41 DO   Let $p(n,k)$ denote the probability that a random function $f : [k]\to [n]$ is an injection (i.e., $\coll(f)=0$). Prove: $$ p(n,k) = \frac{n(n-1)\cdots (n-k+1)}{n^k} = \prod_{i=1}^{k-1}\left(1 - \frac{i}{n}\right)\,. $$

17.42 (Little-omega notation) Let $a_n,b_n$ be sequences of real numbers. We say that $b_n$ is little-omega of $a_n$ and write $b_n =\omega(a_n)$ if $a_n = o(b_n)$, i.e., $a_n/b_n \to 0$.

17.43 (Birthday paradox, asymptotic version) (bonus, due Thursday, Dec 5, 10+10+14 points)

Let $k(n)$ be a function of $n$ and $n\to\infty$. Prove:
(a) If $k(n) = o(\sqrt{n})$ then $\lim_{n\to\infty} p(n,k) = 1$
(b) If $k(n) = \omega(\sqrt{n})$ then $\lim_{n\to\infty} p(n,k) = 0$
(c) If $k(n) = \Theta(\sqrt{n})$ then $p(n,k)$ is bounded away from 0 and 1. In other words, $(\forall c_1,c_2 > 0)(\exists c_3,c_4 > 0) (\exists n_0)(\forall n > n_0)(c_1\sqrt{n} \le k(n) \le c_2\sqrt{n} \implies c_3 \le p(n,k(n)) \le c_4)$
Do not use inequalities other than those stated in these notes.

17.44 (Bell numbers) (Bonus, due Thu, Dec 5, 10 points) Let $B(n)$ denote the $n$-th Bell number (the number of partitions of $[n]$). Prove:   $\ln B(n) \sim n\ln n$. Use Exercises 5.36 and 5.38. Do not use inequalities other than those stated in these notes.

Class 16, Thu 11-21  
Sum of squares of binomial coefficients. Inequalities between various means: harmonic, geometric, arithmetic, quadratic. Expected value, indicator variables. Expected number of successes of a sequence of Bernoulli trials. Positively/negatively correlated, uncorrelated pair of random variables. Variance of a random variable. Cauchy-Schwarz inequality. Covariance of a pair of random variables. Variance of a sum of random variables.
Due Tuesday, 11-26. Also due on Tuesday:  15.7, 15.8, 15.10.

16.1 THEOREM ("Vandermonde's Identity")   $\displaystyle{\sum_{k=1}^n \binom{n}{k}^2 = \binom{2n}{n}}$
The identity was known to 14th century Chinese mathematician Zhu Shijie. See Wikipedia for the history and generalizations.

16.2 DO   Combinatorial proof. We have a set $S$ of $2n$ balls, $n$ of them red, $n$ of them blue. Let $N$ denote the number of $n$-subsets of this set of balls. (1) By definition, $N=\binom{2n}{n}$. (2) Let $A$ be a set of $n$ balls (among $S$). We count the sets $A$ in another way. Let $N_k$ denote the number of those $n$-sets of balls among which we have $k$ red balls. Then $N=\sum_{k=0}^n N_k$. Now there are $\binom{n}{k}$ ways to select $k$ red balls and $\binom{n}{n-k}$ ways to select $n-k$ blue balls, so $N_k = \binom{n}{k}\cdot \binom{n}{n-k}=\binom{n}{k}^2$.

16.3 DO   Algebra proof. Consider the identity $(1+x)^{2n}=(1+x)^n\cdot (1+x)^n$. Expand each side by the Binomial Theorem. Compare the coefficient of $x^n$ on each side.

16.4 DO   Let $X:\Omega\to\rrr$ be a random variable. Prove:   $\min X \le E(X) \le \max X$. Discussion: $E(X)$ is a weighted average of the values of $X$.

16.5 DEF   Let $x_1,\dots, x_n\in\rrr$. The arithmetic mean of $x_1,\dots,x_n$ is $A(x_1,\dots,x_n)=(1/n)\sum_{i=1}^n x_i$.
The quadratic mean of $x_1,\dots,x_n$ is $Q(x_1,\dots,x_n)=\left(A(x_1^2,\dots,x_n^2)\right)^{1/2}= \displaystyle{\sqrt{\frac{1}{n}\cdot\sum_{i=1}^n x_i^2}}$
Let $x_i\ge 0$. The geometric mean of $x_1,\dots,x_n$ is $\left(\prod_{i=1}^n x_i\right)^{1/n}$
Let $x_i > 0$. The harmonic mean of $x_1,\dots,x_n$ is $$H(x_1,\dots,x_n)=\frac{1}{A(1/x_1,\dots,1/x_n)} =\frac{n}{\sum_{i=1}^n \frac{1}{x_i}}$$

16.6 THEOREM   Let $x_i > 0$. Then   $H \le G \le A \le Q$

In solving the special cases below, do not refer to the general case.

16.7 HW (3 points)   Let $x_1, x_2 \ge 0$. Prove: $G(x_1,x_2)\le A(x_1,x_2)$.

16.8 HW (4 points)   Let $x_1,\dots, x_4 \ge 0$. Use 16.7 to prove $G(x_1,\dots,x_4)\le A(x_1,\dots,x_4)$.

16.9 Bonus (4 points)   Let $x_1,\dots, x_3 \ge 0$. Use 16.8 to prove   $G(x_1,x_2,x_3)\le A(x_1,x_2,x_3)$.

16.10 Bonus (4 points)   Prove the inequality $G\le A$ for $n=2^k$ variables and then, using this, for any number of variables. Follow these instructions, do not give the proof via convexity/concavity.

16.11 Bonus (4 points) Prove:   $A(x_1,\dots,x_n)\le Q(x_1,\dots,x_n)$.   Give a direct proof, do not use Cauchy-Schwarz. (2 lines)

16.12 HW (4 points) Let $x_i > 0$. Prove:   $H(x_1,\dots,x_n)\le G(x_1,\dots,x_n)$.   Use the inequality $G\le A$. (One-line proof.)

16.13 HW (How crowded is the bus on average?   8 points) All students of a rural college live in dormitory $D$ at a considerable distance from campus ($C$). The college operates an express bus between $D$ and $C$. There are $n$ students, and on a given day, all of them travel from $D$ to $C$ on the bus. The bus makes $\ell$ rounds during the day. The college president wishes to know how crowded the bus is. She hires two pollsters to find out. The first pollster asks every student, how crowded their bus was (number of students traveling, including the student being interviewed). Then the pollster averages these numbers over the $n$ students, and reports this "traveler average" to the president. The second pollster asks the driver, how many students were on each of the $\ell$ rides from $D$ to $C$, averages those numbers and reports this "driver average" to the president. (We ignore the rides back to the dorm in this exercise.) Prove: the traveler average is always greater than or equal to the driver average. (People on average travel on more crowded buses than the average size of the crowd on a bus.) Set up an exact model, name your variables, express the two averages in terms of your variables, and prove the inequality.

16.14 DO   A car travels on a road that has $k$ segments of equal length. On segment number $i$ the speed of the car if $v_i$. Show that the average speed of the car over the trip is $H(v_1,\dots,v_k)$.

16.15 REVIEW Finite Probability Spaces (FPS) handout, Section 7.7 "Random variables, expected value, indicator variables, Bernoulli trials."

16.16 DEF Expected value (FPS 7.7.2)   Let $X:\Omega\to \rrr$ be a random variable. Recall that its expected value is $\sum_{a\in\Omega} X(a)P(a).$

16.17 DO (FPS 7.7.3)   $E(X) = \sum_{r\in\rrr} r\cdot P(X=r)$.   Note that the event "$X=r$" is the same as $\{a\in\Omega\mid X(a)=r\}$. In yet other words, it is $X^{-1}(r)$.
For the proof, for each $r$, combine all those terms in Def. 16.15 for which $X(a)=r$.   Note that while the number of terms seems infinite, the actual number is the size of the range of $X$. (The rest is zero. Why?)

16.18 DEF   An indicator variable is a $(0,1)$-valued random variable.

16.19 DO (FPS 7.7.9)   There is a bijection between events and indicator variables. The indicator of event $A\subseteq\Omega$ is the variable $\vt_A$ defined by $\vt_A(a)=1$ if $a\in A$ and $\vt_A(a)=0$ of $a\notin A$. This is the same concept as the characteristic function (Def. 2.30). Review characteristic functions.

16.21 DO (FPS 7.7.11)   $E(\vt_A) = P(A)\,.$   Hint. 16.17.

16.22 DEF   "Bernoulli trial" is another name for indicator variables. A value of 1 is called "success" and a value of 0 is called a "failure" of the trial. If $X$ is a Bernoulli trial with probability $p$ of success then $E(X)=p$ according to the preceding exercise.

16.23 DO   Show that the expected number of successes in a sequence of $n$ Bernoulli trials with probability $p$ of success is $np$.   Use Ex. 16.17. Assume the Bernoulli trials are independent.
Proof. (Explain each step!) Let $X$ denote the number of successes. Then $P(X=k) = \binom{n}{k}p^k(1-p)^{n-k}$, and therefore $$E(X)=\sum_{k=0}^n k\binom{n}{k}p^k(1-p)^{n-k} = np\sum_{k=1}^n\binom{n-1}{k-1}p^{k-1}(1-p)^{n-k}=np(p+(1-p))^n = np\,.$$

Note: This was an unintuitive technical proof. Next, we give an intuitive proof of a much stronger result.

16.24 DO   Let $X$ denote the number of successes in a sequence of $n$ Bernoulli trials, where the $i$-th trial has probability $p_i$ of success. Show that $E(X) = \sum_{k=1}^n p_k$. For this result to hold, the Bernoulli trials do not need to be independent.
Proof. Let $Y_i$ denote the $i$-th Bernoulli trial. (Recall that $Y_i$ is the indicator of success of the $i$-th trial.) Then $X=\sum_{i=1}^n Y_i$. (Why?) Now use the Linearity of Expectation (FPS 7.7.6, 7.7.7) and Ex. 16.21.

16.25 WARNING. Events have probability; they do not have expected value. Random variables have expected value; they do not have probability.

16.26 HW (3 points) Let $\vt_A$ and $\vt_B$ denote the indicator variables of events $A$ and $B$, respectively. Prove that $\vt_A\cdot\vt_B=\vt_C$ for some event $C$. Describe $C$ as a very simple expression in terms of $A$ and $B$. No proof required.

16.27 HW (6 points) What is the expected number of Aces in a poker hand? Show all your work. Make sure you give a clear definition of the random variables you introduce; that definition will account for half the credit.   Hint: indicator variables.

16.28 HW (6 points) FPS 7.7.16 (expected number of runs of $k$ heads in a sequence of $n$ coin flips).

16.29 HW (5+2 points) FPS 7.7.22 (marbles in cups)

16.30 HW (8 points) FPS 7.7.18 (Club of 2000)

16.31 STUDY the uniform Erdös--Rényi model of random graphs, FPS Section 7.5.

16.32 HW (8 points) FPS 7.5.2 (c) (probability that vertices 1 and 2 have the same degree)

16.33 STUDY FPS Section 7.8 (variance, covariance, Chebyshev's Inequality)

16.34 DEF   The variance of the random variable $X$ is $\var(X) = E((X-E(X))^2)$

16.35 DO   Prove:   $\var(X) = E(X^2)-(E(X))^2$

16.36 DEF   The covariance of random variables $X$ and $Y$ is $\cov(X,Y)=E(XY) - E(X)E(Y)$.

16.37 DEF   We say that the random variables $X$ and $Y$ are positively (negatively) correlated if $\cov(X,Y)$ is positive (negative, resp.). We say that $X$ and $Y$ are uncorrelated if $\cov(X,Y)=0$.

16.38 DO   Let $X$ be a Bernoulli trial with probability $p$ of success. Prove:   $\var(X)=p(1-p)$.

16.39 Bonus (12 points, due Tue, Dec 3) FPS 7.8.17(b) (number of Aces and number of Spades in a poker hand are uncorrelated)

16.40 STUDY FPS Section 7.9 (independence of a pair of random variables)

16.41 HW (6 points) FPS 7.9.4 (uncorrelated does not imply independent)

16.42 HW (5 points) Read FPS 7.8.17(a) (Aces vs. Spades). Prove: the number of Aces and the number of Spades in the poker hand are NOT independent.

16.43 HW (5 points) Let $X$ denote the number of successes in a sequence of $n$ Bernoulli trials where the $i$-th trial has probability $p_i$ of success. Determine $\var(X)$. Your answer should be a simple formula involving summation (not a closed-form expression).

16.44 HW (1+8+4 points, due Tue, Dec 3) FPS 7.8.21 (variance of the number of triangles). Show all your work.

16.45 Bonus (12 points, due Tue, Dec 3) FPS 7.8.22(a) (strongly negatively correlated events)

Class 15, Tue 11-19  
Asymptotic notation: little-oh, big-Oh, big-Omega, big-Theta notation. Finite probability spaces: random variables, expected value, indicator variables.
Due Thursday, 11-21. Also due Thursday:  14.4, 14.11, 14.13, 14.21, 14.26.

15.1 DO   Study the instructor's Discrete Mathematics Lecture Notes, Chapter 2: Asymptotic notation.

15.2 HW (1+4 points) Prove that the big-Oh relation is transitive:   If $a_n=O(b_n)$ and $b_n=O(c_n)$ then $a_n=O(c_n)$.   The first relation means $(\exists C_1, n_1)(\forall n > n_1)(|a_n|\le C_1|b_n|)$. We call $C_1$ the "hidden constant" and $n_1$ the "hidden threshold" in this definition. (a) State the analogous definitions for the two other relations, with hideen constants $C_2$ and $C_3$ and hidden thresholds $n_2$ and $n_3$.   (B) Give a simple expression for the smallest possible hidden constant $C_3$ in terms of $C_1$ and $C_2$ and the smallest possible hidden threshold $n_3$ in terms of $n_1$ and $n_2$.

15.3 HW (5 points) Find sequences $a_n, b_n >0$ such that $a_n = \Theta(b_n)$ but $\lim_{n\to\infty} a_n/b_n$ does not exist. The example should be simple and easy to verify. No proof required.

15.4 HW (5 points) Assume $L=\lim_{n\to\infty} a_n/b_n$ exists. Prove: If $L \neq 0$ and $L\neq \pm\infty$ then $a_n = \Theta(b_n)$. State the hidden threshold and the hidden constants.   Note that there are two hidden constants in the definition of the $\Theta$ relation: the relation means $(\exists C, c > 0)(\exists n_0)(\forall n >n_0)(c|b_n|\le |a_n|\le C|b_n|)\,$.

15.5 DEF (polynomial growth)   The sequence $a_n$ is said to grow polynomially if $(\exists c, k, n_0)(\forall n > n_0)(|a_n|< cn^k)$.   Note that this is an upper bound.

15.6 DEF (exponential growth)   The sequence $b_n$ is said to grow exponentially if $(\exists c > 0, C > 1, n_0)(\forall n > n_0)(|a_n|> cC^n)$.   Note that this is a lower bound.

15.7 HW (6 points, due Tuesday) Let $a_n > 1$. Prove:  $a_n$ grows polynomially if and only if $\ln a_n = O(\ln n)$.

15.8 HW (4 points, due Tuesday) Let $b_n > 1$. Prove:  $b_n$ grows exponentially if and only if $\ln b_n = \Omega(n)$.

15.9 HW (3 points) Prove: $\ln n = \Theta(\log_2 n)$.

15.10 HW (3+3 points, due Tuesday) Let $a_n = n^{\log_2 n}$. Prove: (a) $a_n$ does not grow polynomially (it grows faster)   (b) $a_n$ does not grow exponentially (it grows slower).

15.11 DO   Study the Finite Probability Spaces (FPS) handout, Section 7.7 "Random variables, expected value, indicator variables, Bernoulli trials."

15.12 HW (3+2+4+4 points) Let us roll two dice. The first one shows the number $X$, the second one the number $Y$. (So $1\le X,Y \le 6$.) Determine (a) $E(X)$   (b) $E(X+Y)$   (c) $E(X^2)$   (d) $E(XY)$.   Show all your work. Express your answers as fractions in their simplest form (like $9/5$ if you get $18/10$). Do not use electronic devices.

Class 14, Thu 11-14  
Walks in graphs. Finite probability spaces. Independence of events.

14.1 DEF (walk) A walk of length $k$ from vertex $x$ to vertex $y$ in a graph $G$ is a sequence $v_0,\dots,v_k$ of vertices such that $v_0=x$, $v_k=y$, and $(\forall i)(1\le i \le k \implies v_{i-1}\sim v_i)$.

14.2 DO   Let $x,y\in V(G)$. Prove: If there exists a walk from $x$ to $y$ then there exists a path between $x$ and $y$. In fact, every shortest walk from $x$ to $y$ is a path (has no repeated vertices).

14.3 DO   Use 14.2 to give a straightforward proof of the transitivity of accessibility.

14.4 HW (9 points, due Thursday) Draw all non-isomorphic 7-vertex trees. State how many non-isomorphic trees you got.   Avoid the two kinds of mistakes: drawing two isomorphic trees and missing a tree. You lose 2 points for each mistake.

14.5 DO   Study the Finite Probability Spaces (FPS) handout.

14.6 DO   Exercises FPS 7.1.2-7.1.10 (union bound), 7.2.2.

14.7 HW (2+2 points) FPS 7.1.5 (d3) (d4)

14.8 HW (4 points) FPS 7.1.6 (b1).   You need to base your proof on formula (7.3) and not on an intuitive understanding of the meaning of the variable $X_i\,$.

14.9 HW (4 points) FPS 7.1.6 (c3).

14.10 Bonus (5 points) FPS 7.1.6 (c4).

14.11 HW (1+2+3+2 points) FPS 7.2.3

14.12 DO   FPS 7.2.4 (Theorem of Complete Probability)

14.13 HW (2+6+2 points, due Thursday) FPS 7.2.5 (Probability of causes)

14.14 DO   FPS 7.3.2.

14.15 HW (3 points) FPS 7.3.4 (independence of complement)

14.16 DO   FPS 7.3.5 (independence of trivial event)

14.17 HW (2 points)   FPS 7.3.6 (die)

14.18 HW (4 points)   FPS 7.3.7 (prime-size uniform space)

14.19 HW (5 points)   FPS 7.3.8 (lower bound on the size of the sample space)

14.20 DO   FPS 7.3.10   (positive/negative correlation reflected in conditional probability)

14.21 HW (8 points, due Thursday) FPS 7.3.11 (correlation of divisibility by 2 and 3). For 5 points partial credit, solve the problem for $n=25, 26$ and $29$.

14.22 HW (3 points) FPS 7.3.12 (inclusion vs. independence)

14.23 HW (3 points) FPS 7.3.13 (union, intersection independent)

14.24 DO   FPS 7.4.3 (independence of complement)

14.25 DO   FPS 7.4.4 (independence of trivial event)

14.26 HW (3+3 points, due Thursday) FPS 7.4.5 (independence of intersection, union)

14.27 Bonus (4 points) FPS 7.4.6 (lower bound on the size of the sample space)

14.28 HW (1+6 points) FPS 7.4.7 (pairwise but not fully independent events)

14.29 HW (4 points) FPS 7.4.8 (a) (intersection of 3 events)

14.30 Bonus (3 points) FPS 7.4.8 (b) (intersection of 3 events)

Class 13, Tue 11-12  
Trees. Induction on graphs. Independence number. Chromatic number.
Due Thursday, November 14. Recall that the following problems are also due on Thursday: 12.47(B), 12.53, 12.54, 12.55, 12.56(B), 12.57(B).

13.1 DEF   A tree is a connected, cycle-free graph.

13.2(a) DEF: The star graph $\star_n$ with vertex set $V=\{v_0,\dots,v_{n-1}\}$ has edge set $E=\{\{v_0,v_i\}\mid 1\le i\le n-1\}$. (One central vertex is adjacent to all other vertices, and no two of those other vertices are adjacent.)
13.2(b) Examples of trees: the path $P_n$ and the star graph are trees.

13.3 THEOREM.   A tree with $n\ge 1$ vertices has $m=n-1$ edges.

The proof is based on the following two lemmas.

13.4a DEF   A pendant vertex is a vertex of degree 1. (WARNING: in class I called such a vertex a "dangling vertex" but the official term is "pendant vertex.")

13.4b Pendant Vertex Lemma.  If a tree has $n\ge 2$ vertices then it has a pendant vertex.

13.5 NOTATION. Let $G=(V,E)$ be a graphs and $v\in V$. Then $G-v$ is that graph we obtain by deleting $v$ from $V$ and deleting all edges incident with $v$ from $E$. So $G-e$ has $n-1$ vertices and $m-\deg(v)$ edges. (DO: Verify!)

13.6 DO Lemma.   Let $G$ be a connected graph with a pendant vertex $v$. Then $G-v$ is connected.

13.7 Proof of Theorem 3.3 based on Lemmas 13.4 and 13.6. Let $T$ be a tree with $n\ge 1$ vertices. We show by induction on $n$ that $m=n-1$. The base case: If $n=1$ then $m=0$. For the inductive step, assume $n\ge 2$ and the Theorem it true for all trees with $n' < n$ vertices (Inductive Hypothesis). Our input is a tree $T$ with $n\ge 2$ vertices. Let $v$ be a pendant vertex of $T$ - such a vertex exists by Lemma 13.4. Let $T'=T-v$.
Claim. $T'$ is a tree.
Indeed, (a) $T'$ is cycle-free (because $T'$ is a subgraph of $T$, and $T$ is cycle-free). Moreover, $T'$ is connected by Lemma 13.6. This proves the Claim.
Now, $T'$ has $n'=n-1$ vertices and $m'=m-1$ edges. By the Inductive Hypothesis, $m'=n'-1$. Therefore $m-1 = =m' = n'-1 = (n-1)-1$. Adding 1 to the each side of this equation we get $m=n-1$, the desired conclusion. QED

What is left to prove is Lemma 13.4. (13.6 is a DO exercise.) For the proof of 13.4 we use exercise 13.11 below.

13.8 DEF   A maximal path in a graph is a path that cannot be extended to a longer path. A maximum path is a longest path.

13.9 DO   Every maximal path in a graph is maximum. -- The converse is false, as the next exercise asserts.

13.10 HW (4 points) Find a tree $T$ and a maximal $P$ in $T$ such that $P$ is not a maximum path in $T$. Make your tree as small as possible.

13.11 HW (1+3 points) Let $P$ be a maximum path in a tree with $n\ge 2$ vertices. Prove that (a) $P$ has length $\ge 1$ and (b) the endpoints of $P$ have degree 1 in $T$.

13.12 DO   Use 13.11 to prove Lemma 13.4. This completes all details of the proof of Theorem 13.3.

13.13 DEF   Let $H=(W,F)$ be a subgraph of $G=(V,E)$. We say that $H$ is a spanning subgraph of $G$ if $V=W$ (we may delete edges but we cannot delete vertices). A spanning subgraph that is a tree is called a spanning tree.

13.14 HW (3 points) Count the spanning subgraphs of the graph $G$. Your answer should be a very simple formula in terms of the basic parameters $n,m$ of $G$. No proof required.

13.15 THEOREM.   A graph $G$ has a spanning tree if and only if $G$ is connected.

13.16 DO   Necessity is clear. Prove sufficiency: Every connected graph has a spanning tree.   -- Hint. Give an algorithmic proof: "grow" a subtree in $G$. While your subtree is not spanning, show that you can add an edge.

13.17 NOTATION   Let $G=(V,E)$ be a connected graph and $e\in E$. Then $G-e$ denote the subgraph with $V(G-e)=V$ and $E(G-e)=E(G)$ (we delete the edge $e$ but do not delete any vertices). So $G-e$ is a spanning subgraph.

13.18 DO   Let $G$ be a connected graph and let $e\in E(G)$. Then $G-e$ is connected if and only if $e$ belongs to a cycle.   Hint. For the sufficiency, use prove and use Exrcise 13.20 below.

13.19 DEF   Let $G$ be a graph and $s,t\in V(G)$. A walk of length $k$ from $s$ to $t$ is a sequence of vertices, $v_0,v_1,\dots,v_k$, such that $v_0=s$, $v_k=t$, and $(\forall i)(1\le i\le k \implies v_{i-1}\sim v_i)$. ($s$ is the start vertex of the walk and $t$ is the terminus of the walk.)

13.20 DO   Prove: vertex $t$ is accessible from vertex $s$ in the graph $G$ if and only if there exists a walk from $s$ to $t$.   Hint. Prove and use the next exercise.

13.21 DO   A shortest walk from $s$ to $t$ defines a path connecting $s$ to $t$: If $s=v_0,\v_1,\dots,v_k=t$ is a shortest $s\to t$ walk then the subgraph $H$ with $V(H)=\{v_0,\dots,v_k\}$ and $E(H)=\{\{v_{i-1},v_i\}\mid 1\le i\le k\}$ is a path connecting $s$ to $t$.

13.22 DO   Use 13.20 to give a simple proof of transitivity of accessibility.

13.23 HW (4 points) Let $G$ be a connected graph and $H$ a minimal connected spanning subgraph of $G$. This means that $H$ is a connected spanning subgraph of $G$ but for any $e\in E(H)$, the graph $H-e$ is disconnected. Prove: $H$ is a spanning tree.   Do not use Theorem 13.15.

13.24 DO   Use 13.23 to give an alternative proof of Theorem 13.15.

13.25 DO   Prove: A graph is a tree if and only if there is a unique path between each pair of vertices.

13.26 DO   Prove: up to isomorphism, there are exactly 2 trees with 4 vertices: the path $P_4$ and the star graph $\star_4$ (see DEF 13.2(a)). - What "up to isomorphism" means is that every 4-vertex tree is isomorphic either to $P_4$ or to $\star_4$.

13.27 DO   The number of spanning trees of $K_4$ is $16$. Out of these, $4$ are isomorphic to $\star_4$ and $12$ are isomorphic to $P_4$ (prove!).

13.28 DO   Prove: the number of spanning trees of $K_5$ is $125$. -- Hint. First, find all 5-vertex trees up to isomorphism. There are only three.

13.29 CAYLEY's formula.   The number of spanning trees of $K_n$ is $n^{n-2}$.

13.30 DO   For a bijective proof, look up Prüfer's code.

13.31 DO   Let $d_1,\dots,d_n$ be the degrees of the vertices of a tree with $n$ vertices. Prove:   $\sum_{i=1}^n d_i = 2n-2$.   Hint: Handshake Theorem.

13.32 DO   Let $d_1,\dots,d_n$ be positive integers such that $\sum_{i=1}^n d_i = 2n-2$. Prove: the number of trees with vertex set $V=[n]$ such that $\deg(i)=d_i$ is $$ \frac{(n-2)!}{\prod_{i=1}^n (d_i-1)!}$$ Hint. Careful induction on $n$.   Understand this formula even if you don't prove it. Prove it if you are shooting for an A or A- in the course.

13.33 DO   (multinomial theorem) Generalize the Trinomial Theorem (Exercise 12.3) to $k$ terms: find the expansion of $(x_1+\dots +x_k)^n$: $$ (x_1+\dots +x_k)^n = \sum_{\substack{i_1,\dots,i_k\ge 0\\ \sum_j{i_j}=n}} a(i_1,\dots,i_k) x_1^{i_1}\cdots x_k^{i_k} $$ where the coefficient $a(i_1,\dots,i_n)$ is the multinomial coefficient (DO: review Theorem 9.12). $$ a(i_1,\dots,i_k) = \binom{n}{i_1,\dots,i_k} = \frac{n!}{\prod_{j=1}^k i_j!} $$

13.34 Bonus (5 points, due Tuesday) Use Exercise 13.32 to prove Cayley's formula. The proof should be just one line.

13.35 DO   A connected graph has $m\ge n-1$ edges.   Hint: Use Theorem 13.15 (existence of a spanning tree).

13.36 HW (5 points, due Tuesday) Prove: If the graph $G$ has $k$ connected components then it has at least $n-k$ edges.

13.37 DEF   An independent set in a graph $G=(V,E)$ is a subset $S\subseteq V$ such that there are no edges joining vertices in $S$, i.e., $(\forall x,y\in S)(x\not\sim y)$. The size of the largest independent set is called the independence number of $G$. It is denoted $\alpha(G)$ ($\alpha$ is the first letter of the Greek alphabet, called "alpha").

13.38 DO   $\alpha(K_n)=1$ and $\alpha(\overline{K_n})=n$.

13.39 DO   Prove:   $\alpha(P_n)=\lceil n/2\rceil$

13.40 HW (due Tuesday, 5 points)   Prove:   $\alpha(C_n)=\lfloor n/2\rfloor$.   Give an elegant proof of the upper bound.
Hint. To prove the upper bound, you only need to prove for every independent set $A\subseteq V(C_n)$ the inequality $|A|\le n/2$. (Why is this sufficient?) - Imagine a fairy is sitting at each node of $A$ and a dwarf sitting on each edge of $C_n$. So there are $n$ dwarfs and $|A|$ fairies. Initially each fairy has two chocolate bars. The fairy gives one chocolate bar to each dwarf sitting next to her (on the two edges incident with her node). Now the fairies have no chocolate bars left, all the chocolate bars are held by the dwarfs. How many chocolate bars does each dwarf have?

13.41 Bonus (5 points, due Tuesday) Prove: If $G$ is a regular graph of degree $\ge 1$ then $\alpha(G) \le n/2$.

13.42 DO   A subset of an independent set is an independent set. (Note: this includes the fact that the empty set is independent!)

13.43 HW (2+6 points, due Tuesday) Count the independent sets in $P_n$. (Don't forget to include the empty set in your count.) Let $z_n$ denote this number. (a) List the values $z_n$ for $n\le 4$. No proof required. (b) Discover a pattern, make a conjecture, prove it. (Work out part (a) carefully; if you make a mistake there, you will miss the pattern.) Give $z_n$ a very simple expression in terms of a familiar sequence.

13.44 DO   If $A$ is an independent set in $G$ then $A$ is a clique in $\Gbar$.

13.45 DEF   A maximal independent set in the graph $G=(V,E)$ is an independent set that cannot be extended. In other words, it is a subset $A\subseteq V$ such that (a) $A$ is independent and (b) if $A\subseteq B\subseteq V$ and $B$ is independent then $B=A$.
A maximum independent set

13.46 HW (5 points, due Tuesday) Let $m(G)$ denote the size of the smallest maximal independent set of the graph $G$. Determine $m(C_n)$.

13.47 HW (5 points, due Tuesday) For every $n\ge 2$ find the maximum possible value of $\alpha(G)/m(G)$ where the maximum is taken over all graphs with $n$ vertices. For each $n$ you need to exhibit a graph which attains this maximum value.

13.48 Bonus (5 points, due Tuesday) Determine $\alpha(\grid(k,\ell))$. Give elegant, short proofs of the lower as well as of the upper bounds. Avoid cumbersome counting.

13.49 DEF   A coloring of the vertices of a graph $G$ is a function $f: V(G)\to C$ where $C$ is a set to which we refer as the set of "colors." A legal coloring is a coloring of the vertices such that adjacent vertices get different colors. In other words, the coloring $f$ is legal if $(\forall x,y\in V(G))(x\sim y \implies f(x)\neq f(y))$. The graph is $k$-colorable if a set $C$ of size $k$ suffices for a legal coloring. The chromatic number $\chi(G)$ is the smallest $k$ such that $G$ is $k$-colorable. ($\chi$ is the Greek letter chi, pronounced "khi".)

13.50 DO   $G$ is $k$-colorable if and only if $k\ge \chi(G)$.

13.51 DO   The chromatic number of $G$ is the smallest value $k$ such that $V(G)$ has a partition into $k$ independent sets.

13.52 DO   $1\le \chi(G)\le n$.

13.53 DO   $\chi(K_n)=n$ and $\chi(\overline{K_n})=1$.

13.54 DO   If $\chi(G)=n$ then $G$ is the complete graph. If $\chi(G)=1$ then $G$ is the empty graph ($\overline{K_n}$).

13.55 DO   $\chi(P_n)=2$ if $n\ge 2$.  $\chi(P_1)=1$.

13.56 DO   Let $n\ge 3$. $\chi(C_n)=2$ if $n$ is even and $\chi(C_n)=3$ if $n$ is odd.

13.57 HW (6 points, due Tuesday) Let $\Delta(G)=\max_{v\in V(G)}\deg(v)$ denote the maximum degree of the graph $G$. Prove:   $\chi(G) \le 1+\Delta(G)$.

13.58 HW (4 points, due Tuesday) The chromatic number is often much smaller than the upper bound $1+\Delta(G)$ in the preceding exercise. For every even value of $n\ge 2$ find a graph $G$ with $n$ vertices such that $\Delta(G)=n/2$ and $\chi(G)=2$.

13.59 HW (4 points, due Tuesday)   $\alpha(G)\cdot \chi(G) \ge n$.

13.60 HW (4 points, due Tuesday) Show that for every $n\ge 2$ there is a graph $G$ such that $\alpha(G)\cdot \chi(G) \ge n^2/4.$

13.61 Bonus (7 points, due Tuesday) Prove: If $G$ is triangle-free then $\chi(G) \le 1+2\sqrt{n}$.

13.62 DEF   A clique of size $k$ in a graph is a complete subgraph with $k$ vertices. (A clique of size 3 is a triangle.)

13.63 DO   If $G$ contains a clique of size $k$ then $\chi(G)\ge k$.

This observation raises the question, is it possible for a graph to have no large cliaues yet have large chromatic number? The surprising answer is "yes." We begin addressing this question in the next two problems.

13.64 HW (1+4 points) A clique of size $k$ in a graph is a complete subgraph with $k$ vertices. (A clique of size 3 is a triangle.) (a) Find the smallest triangle-free graph that is not 2-colorable.   (b) Find the smallest graph without a 4-clique that is not 3-colorable. - Give a nice drawing for each question. (A hand drawing suffices.) For (a), no proof is required. For (b), prove that your graph is not 3-colorable.

13.65 Bonus (6 points, due Tuesday) Construct a triangle-free graph which is not 3-colorable. Let your graph have 11 vertices and admit a placement of the vertices in the plane so as to admit a 5-fold rotational symmetry. This means that if we rotate the plane by $2\pi/5$ (72 degrees) then the graph turns into itself. (For instance you can put the vertices of $C_5$ in the plane this way, and also the vertices of the Petersen graph shown in the first picture in Exercise 12.53.) Draw a nice picture (by hand). Prove that your graph is not 3-colorable.

13.66 CH   For every $k$ there exists a triangle-free graph that is not $k$-colorable.

13.67 DEF   A bipartite graph is a 2-colorable graph.

13.68 DO   A graph is bipartite if and only if the set of vertices is the union of two independent sets.

13.69 DO   The cycle $C_n$ is bipartite if and only if $n$ is even.

13.70 DO   The grid graphs are bipartite.

13.71 HW (5 points) Every tree is bipartite. -- Prove this by induction on $n$. Use the Pendant Vertex Lemma (Exercise 13.4).

13.72 DO   A bipartite graph has no odd cycles.

13.73 THEOREM (characterization of bipartite graphs)  A graph is bipartite if and only if it has no odd cycles.

13.74 DO: prove this theorem. The necessity is trivial (Exercise 13.72). For the sufficiency, note that it suffices to prove it separately for each connected component. So WLOG we may assume the graph is connected. Now use a spanning tree.

13.75 DEF   The complete bipartite graph $K_{r,s}$ $(r,s\ge 1)$ has $n=r+s$ vertices; each of the first $r$ vertices is adjacent to each of the last $s$ vertices. The are no other edges, so the set of the first $r$ vertices is independent, and so is the set of the last $s$ vertices.

13.76 DO   $K_{r,s}$ has $m=rs$ edges.

13.77 DO   $K_{r,s}$ is bipartite.

13.78 DO   Every bipartite graph is a spanning subgraph of a complete bipartite graph.

13.79 DO   The star graph is a complete bipartite graph:   $\star_n \cong K_{1,n-1}$.

13.80 Bonus (6 points, due Tuesday) The union $G\cup H$ of the graphs $G=(V,E)$ and $H=(W,F)$ is the graph $(V\cup W, E\cup F)$. Prove:   $\chi(G\cup H)\le \chi(G)\cdot\chi(H)$.

13.81 Bonus (4 points, due Tuesday) Prove: If $K_n$ is the union of $k$ bipartite graphs then $k \ge \log_2 n$.

13.82 HW (2+5 points, due Tuesday) Prove: (a) $K_4$ is the union of two trees.   (b) If $K_n$ is the union of $k$ trees then $k\ge n/2$.

Class 12, Thu 11-7  
Binomial Theorem proved. Trinomial Theorem. Graph Theory: basic concepts. Adjacency, degree. Handshake Theorem. Incidence, incidence matrix, proof by Accountant's principle. Subgraph, complement. Isomorphism. Paths, cycles, cliques. Grid graph. Accessibility, connected components. Triangle-free graphs. Counting monotone functions.
Due Tuesday, November 12. Recall that problems 11.2, 11.3, 11.9, 11.11, 11.12, 11.13, 11.16, 11.26, 11.27, 11.30, 11.37 are also due on Nov 14.

12.1 Bonus (5 points) Prove: $(\forall k\ge 0)(\forall n)(k! \mid n(n+1)\dots(n+k-1))$. In words: $k!$ divides the product of any $k$ consecutive integers.   The essence of the proof is one line, complete proof two lines. Proofs that take more than 4 lines get diminishing credit.

12.2 DO   Review the proof of the Binomial Theorem given in class, based on counting permutations with repeated items.

12.3 HW (5 points) State and prove the Trinomial Theorem: the expansion of $(x+y+z)^n$ as a sum of the form $$ \sum_{\substack{i,j,k \ge 0 \\ i+j+k = n}} a(i,j,k)\cdot x^iy^jz^k $$ where the coefficients $a(i,j,k)$ are positive integers. It is clear that each expansion term is of the form $x^i y^j z^k$ where the exponent are nonnegative integers that add up to $n$. The question is, how many times $x^i y^j z^k$ will occur as an expansion term; this number is the coefficient $a(i,j,k)$. Your job is to determine the number $a(i,j,k)$. Your answer should be a simple expression in terms of $i,j,k,n$. The expression will involve factorials. Indicate the idea of the proof.

12.4 HW (4 points) Count the terms in the Trinomial Theorem. Your answer should be a simple expression in terms of $n$.

12.5 DEF   A graph $G$ consists of a set of vertices (singular: vertex) together with an irreflexive, symmetric relation called adjacency and denoted $\sim_G$. So if vertices $i$ and $j$ are adjacent, we write $i\sim_G j$ or simply $i\sim j$ if the graph in question is clear from the context. If $i\sim j$, we say that the pair $e=\{i,j\}$ is an edge. In this case we also say that $i$ and $j$ are joined by the edge $e$. We write $G=(V,E)$ where $V$ is the set of vertices and $E$ is the set of edges. We also write $V(G)$ and $E(G)$ for the set of vertices and edges of $G$, respectively. Adjacent vertices are also called neighbors, and the number of neighbors of vertex $x\in V$ is called the degree of $x$, denoted $\deg_G(x)$ or simply $\deg(x)$.

12.6 NOTATIONAL CONVENTION.   Most of the time in this course we write $n=|V|$ (number of vertices) and $m=|E|$ (number of edges).

12.7 DO   $0\le m\le \binom{n}{2}$

12.8 HW (3 points) Count the graphs on a given set of $n$ vertices $(n\ge 0).$ Your answer should be a very simple expression in terms of $n$. No proof required.

12.9 HW (4 points) Count the graphs on a given set of $n$ vertices $(n\ge 0)$ with a given number $m$ of edges $(m\ge 0)$. Your answer should be a rather simple expression in terms of $n$ and $m$. No proof required.

12.10 DO (Handshake Theorem)   $\sum_{x\in V} \deg(x) = 2m$.

12.11 DO Corollary.   The number of vertices of odd degree is even.

12.12 DEF The complete graph on a given set of $n$ vertices is the graph where each pair of vertices is adjacent, so $m=\binom{n}{2}$. The generic notation for the complete graph on $n$ vertices is $K_n$. This notation does not specify the set of vertices; unless otherwise specified, we may take $V=[n]$.   A complete graph is also called a clique and $K_n$ is called an $n$-clique.

12.13 DEF The path of length $n-1$, denoted $P_n\,$ $(n\ge 1)$, has $n$ vertices and $n-1$ edges that join consecutive pairs vertices. If we take $V=[n]$ and $E=\{\{1,2\},\{2,3\},\{3,4\},\dots,\{n-1,n\}\}$, we get $P_n$. 12.14 DO   Note that $P_1=K_1$ has just one vertex and no edges. Note also that $P_2 = K_2$ has two vertices, joined by an edge.

12.15 DEF The cycle of length $n$, denoted $C_n\,$, $(n\ge 3)$, has $n$ vertices and $n$ edges. It can be defined by taking the path $P_n$ and joining the two vertices of degree 1. So if we take $V=[n]$ and $E=\{\{1,2\},\{2,3\},\{3,4\},\dots,\{n-1,n\},\{n,1\}\}$, we get $C_n$.
$C_n$ is also called an $n$-cycle. A 3-cycle is also called a triangle.

12.16 DO   Note that a cycle has at least 3 vertices. Note also that $C_3 = K_3$.

12.17 DEF   We say that vertex $i$ is incident with edge $e$ if $i\in e$.

12.18 DEF The incidence matrix of the graph $G=(V,E)$ is an $n\times m$ $(0,1)$ matrix (every entry is zero or one) where the rows correspond to the vertices and the columns correspond to the edges. The entry in row $i$ and column $e$ is 1 if vertex $i$ is incident with edge $e$, and zero otherwise.

12.19 HW (4 points) Write down the incidence matrix of each of the following graphs: $K_4$, $P_5$, $C_5$.

12.20 DO   (a) The sum of row $i$ in the incidence matrix is $\deg(i)$.   (b) The sum of each column in the incidence matrix is 2.

12.21 DO   Use the preceding exercise to prove the Handshake Theorem. Use the Accountant's Principle: If you add up each row sum in a matrix, or you add up each column sum, you get the same number (namely, the sum of all entries of the matrix).

12.22 DEF   The complement of the graph $G=(V,E)$ is the graph $\Gbar=(V,R')$ where for $i\neq j\in V$, adjacency is defined by $i\sim_{\Gbar} j \iff i\not\sim_G j$.

12.23 DO   (a) $m_G + m_{\Gbar} = \binom{n}{2}$. (Here $m_G$ denotes the number of edges of the graph $G$.)   For each vertex $i\in V(G)$ we have $\deg_G(i)+\deg_{\Gbar}(i) = n-1$.

12.24 DEF   The empty graph is defined as $(V,\emptyset)$ (it has no edges). It is the complement of the complete graph.

12.25 DEF   The graph $H=(W,F)$ is a subgraph of the graph $G=(V,E)$ if $W\subseteq V$ and $F\subseteq E$.

12.26 HW (5 points) Count the subgraphs of $K_n$. This will not be a closed-form expression but a simple summation of a simple expression. Explain the terms of your formula (what does each term count?). No proof beyond this explanation is required.

12.27 DEF (isomorphism)   Let $G=(V,E)$ and $H=(W,F)$ be graphs. An isomorphism from $G$ to $H$ is a bijection $f : V\to W$ that preserves the adjacency relation, i.e., $(\forall i,j\in V)(i\sim_G j \iff f(i)\sim_H f(j))$. We say that the graphs $G$ and $H$ are isomorphic if there exists and isomorphism between them. If this is the case, we write $G\cong H$.

12.28 DO   Prove: Isomorphism (the relation of being isomorphic) is an equivalence relation among graphs: (a) $G\cong G$   (b) if $G\cong H$ then $H\cong G$   (c) if $G\cong H$ and $H\cong K$ then $G\cong K$.

12.29 DO   If $G\cong H$ then $n_G=n_H$ and $m_G=m_H$. In words: isomorphic graphs have the same number of vertices and the same number of edges.

12.30 DO   Isomorphism preserves the degrees of the vertices. More precisely, if $G=(V,E)$ and $H=(W,F)$ and $f:V\to W$ is a $G\to H$ isomorphism then $(\forall i\in V)(\deg_G(i)=\deg_H(f(i))$.

12.31 HW (4 points) Find two non-isomorphic graphs with 4 vertices each and with the same number of edges. Minimize the number of edges of your graphs. Prove that they are not isomorphic.

12.32 DO All cliques with $n$ vertices are isomorphic.

12.33 DEF Every graph that is isomorphic to $P_n$ is called a path of length $n$. Every graph that is isomorphic to $C_n$ is called a cycle of length $n$ (or an $n$-cycle). Every 3-cycle is called a triangle.

12.34 HW (1+5 points) (a) Count the triangles in $K_n$. Your answer should be a very simple formula; no proof required.   (b) Count the $k$-cycles in $K_n$ (i.e., count the subgraphs of $K_n$ that are isomorphic to $C_k$). Your answer should be a simple closed-form expression; binomial coefficients and factorials are permitted primitives. Explain your formula. Check that your formula gives the correct answer for $k=3$.

12.35 DEF A graph is regular if each vertex has the same degree. The graph is $d$-regular if each vertex has degree $d$.

12.36 DO   $K_n$ is $(n-1)$-regular. The empty graphs are regular of degree $0$. The cycles are regular of degree $2$. The paths of length $\ge 2$ are not regular.

12.37 DO   Prove: if $G$ is $d$-regular then $\Gbar$ is $(n-d-1)$-regular.

12.38 DO   If two regular graphs are isomorphic, they must have the same degree.

12.39 HW (5 points) Find two regular graphs of the same degree that have the same number of vertices but are not isomorphic. Make your graphs as small as possible (smallest number of edges). Prove that your graphs are not isomorphic.

12.40 DEF   We say that vertex $j$ is accessible from vertex $i$ if there is a path between them.

12.41 HW (connected components) (7 points) Prove: the accessibility relation is an equivalence relation on $V(G)$. Reflexivity follows by having a path $P_1$ between $i$ and $i$. Symmetry is clear (go the same path backwards). Your job is to prove transitivity. This is less obvious than it seems. Can you think of an alternative characterization of accessibility that will make transitivity immediate? -- The equivalence classes are called connected components.

12.42 DEF   A graph $G$ is self-complementary if $G \cong \Gbar$.

12.43 DO   Prove that $P_4$ and $C_5$ are self-complementary.

12.44 HW (4 points) Prove: if $G$ is self-complementary then $n\equiv 0$ or $1 \pmod 4$.

12.45 DEF   A graph is triangle-free if it has no triangles. For instance, $C_n$ is triangle-free for $n\ge 4$.

12.46 DO   Let $G$ be a triangle-free graph. Let $i,j\in V(G)$. Prove: if $i\sim j$ then $\deg(i)+\deg(j)\le n$.

12.47 Bonus (due Thursday, 6 points) Prove: If $G$ is triangle-free then $m\le n^2/4$.   Hint. Induction on $n$. For the inductive step, remove a pair of adjacent vertices. Use the preceding exercise.

12.48 DEF   The $k\times\ell$ grid graph $\grid(k,\ell)$ has $k\ell$ vertices arranged in a $k\times\ell$ grid; vertical (North/South) and horizontal (East/West) neighbors are adjacent. More precisely, $V=[k]\times[\ell]$ and vertices $(i_1,j_1)$ and $(i_2,j_2)$ are adjacent if $|i_1-i_2|+|j_1-j_2|=1$.

12.49 DO   If $k,\ell \ge 2$ then every vertex in $\grid(k,\ell)$ has degree 2, 3, or 4; exactly four vertices have degree 2 (the four corners).

12.50 HW (4 points) Determine the number of edges of $\grid(k,\ell)$. Your answer should be a formula of the form $ak\ell+bk+c\ell+d\,$; your job is to determine the coefficients $a,b,c,d$. (The coefficients are constants, they do not depend on $k$ or $\ell$.) Prove your answer.

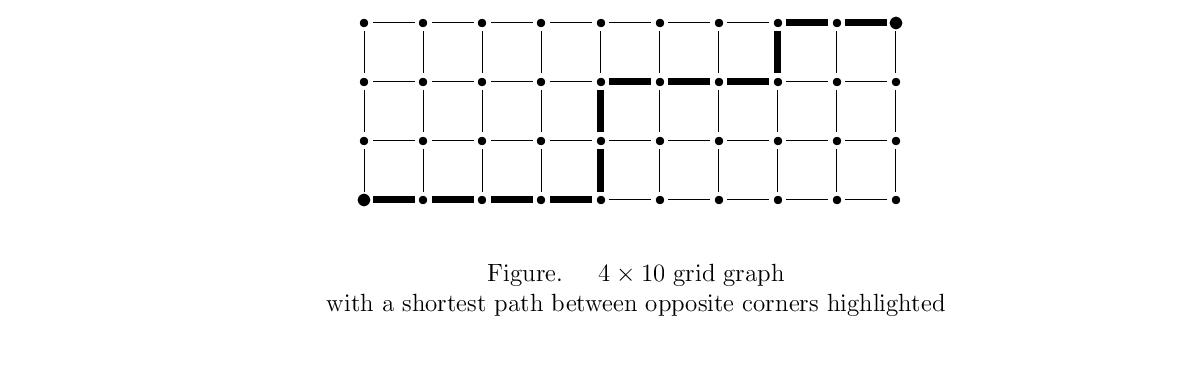
12.51 DO   The length of any shortest path between two opposite corners of $\grid(k,\ell)$ is $k+\ell-2$. (See Figure below.)

12.52 HW ("Manhattan walk problem," 5 points) Count the shortest paths from the bottom left corner to the top right corner of $\grid(k,\ell)$. Your answer should be a very simple formula involving binomial coefficients. Give a bijective proof of your answer.

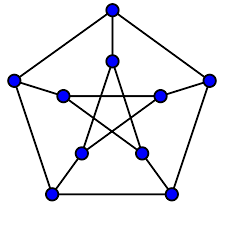
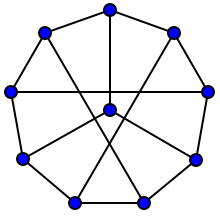
12.53 HW (5 points, due Thursday) Each graph in the images below has 10 vertices and is regular of degree 3. Are they isomorphic? Prove your answer.

12.54 HW (4 points, due Thursday) How many ways can we distribute $n$ identical chocolate bars to $k$ children so that each child receives at least 2 chocolate bars? In other words, count the integer solutions to the equation $\sum_{i=1}^k w_i = n$ under the constraint $(\forall i)(w_i\ge 2)$. Your answer should be a simple formula involving binomial coefficients. Give a very simple proof by reduction to a problem we have already solved.

12.55 HW (4+4 points, due Thursday) Let $n,k\ge 0$. Note: $[0]$ is the empty set.   A function $f:[n]\to [k]$ is monotone increasing if $(\forall x,y\in [n])(x\ge y \implies f(x)\ge f(y))$. It is strictly increasing if $(\forall x,y\in [n])(x > y \implies f(x) > f(y))$.
(a) Count the strictly increasing functions $[n]\to [k]$. Give a one-line solution.)   (b) Count the monotone increasing functions $[n]\to [k]$. Give a very simple bijective solution using part (a).
Your answer to each question should be a simple formula involving binomial coefficients.

12.56 Bonus (5 points, due Thursday) Prove: if the graph $G$ is disconnected (not connected) then $\Gbar$ is connected.

12.57 Bonus (6+1 points, due Thursday) (a) Prove: if both the graph $G$ and its complement are triangle-free then $n\le 5$. (b) Show that this bound is tight. What does this mean?

Class 11, Tue 11-5  
Infinitude of primes. Primes in arithmetic progressions. Inequalities for binomial coefficients. Counting, "stars and bars." Limits. Asymptotic equality. Prime Number Theorem, Stirling's formula.
Due Thursday, November 7, along with 10.35 and 10.38.

11.1 THEOREM (Euclid, 300 BCE)   There are infinitely many primes.
Proof by contradiction: assume $S=\{p_1,\dots,p_k\}$ is the set of all primes. Let $P=\prod_{i=1}^k p_i$. Let $q$ be a prime divisor of $P+1$. So $P\equiv -1 \pmod q$. But $q\in S$ (because $S$ contains all primes), so $q\mid P$ and therefore $P\equiv 0\pmod q$. Therefore $-1\equiv 0 \pmod q$, so $q\mid 1$, a contradiction. QED

11.2 Bonus (5 points, due Tuesday) Prove that there are infinitely many primes $p\equiv -1 \pmod 4$.

11.3 Bonus (5 points, due Tuesday)   Prove: if $p$ is an odd prime and $(\exists x)(x^2\equiv -1 \pmod p)$ then $p\equiv 1\pmod 4$.
Hint. Fermat's little Theorem.

11.4 CH   Prove that there are infinitely many primes $p\equiv 1 \pmod 4$.

11.5 DO   Consider the arithmetic progression $a, a+d, a+2d, \dots$ where $d\neq 0$. Prove: if $\gcd(a,d)\neq 1$ then there is at most one prime number in the progression.

The converse is one of the most remarkable results in number theory.

11.6 THEOREM (Dirichlet, 1837)   If $d > 0$ and $\gcd(a,d)=1$ then there are infinitely many primes $p\equiv d \pmod a$.

11.7 HW (5 points) Let $1\le k \le n/2$. Prove: $$ \binom{n}{k-1} < \binom{n}{k} $$

11.8 HW (3 points) Let $n\ge 0$. Prove: $$ \binom{2n}{n} \le 4^n $$ Hint. Look at the sum of row number $2n$ in Pascal's triangle.

11.9 HW (4 points, due Tuesday) Let $n\ge 0$. Prove: $$ \binom{2n}{n} \ge \frac{4^n}{2n+1} $$ Hint. Two preceding exercises.

11.10 HW (2 points) Let $1\le k\le n$. Prove: $$ \binom{n}{k} \le \frac{n^k}{k!} $$

11.11 HW (4 points, due Tuesday) Let $1\le k\le n$. Prove: $$ \binom{n}{k} \ge \left(\frac{n}{k}\right)^k $$

11.12 (Bonus, 3 points, due Tuesday) For $n\ge 0$, prove: $\displaystyle{n! \ge \left(\frac{n}{\eee}\right)^n}$. Use the power series expansion $\displaystyle{\eee^x =\sum_{k=0}^{\infty} \frac{x^k}{k!}} \,.$   (One-line proof.)

11.13 (Bonus, 3 points, due Tuesday) Let $1\le k\le n$. Prove: $$\binom{n}{k} \le \left(\frac{\eee n}{k}\right)^k $$

11.14 FACT (Euler's identity)   $1+\eee^{i\pi} = 0$
connects the five most important numbers ($0,1,\pi,\eee, i=\sqrt{-1}$)
This follows from Euler's identity $\eee^{it}=\cos t + i\sin t\,$ $(t\in\rrr)$

11.15 (Stars and bars) How many ways can we distribute $n$ identical choclate bars among $k$ kids? Equivalently, count the integer solutions of the equation $\sum_{i=0}^k x_i = n$ under that constraint $x_i\ge 0$.
Solution (bijective).   The "stars and bars" trick gives a bijection between the solutions to the problem and the strings of length $n+k-1$ over the binary alphabet $\{*,|\}$ consisting of $n$ stars and $k-1$ bars, so the number is $\binom{n+k-1}{n} = \binom{n+k-1}{k-1}$.

11.16 HW (5 points, due Tuesday) Count the integer solutions of the equation $\sum_{i=0}^k y_i = n$ under that constraint $y_i\ge 1$ (each kid gets at least one chocolate bar).

11.17 DEF Let $(a_n \mid n\in \nnn)$ be a sequence. We say that this sequence is eventually non-zero if $a_n\neq 0$ for all sufficiently large $n$, i.e., if $(\exists n_0)(\forall n > n_0)(a_n\neq 0)$.

11.18 DEF We say that $\lim_{n\to\infty} a_n = L$ if $(\forall \epsilon > 0)(\exists n_0)(\forall n > n_0)(|a_n - L| <\epsilon)$. (Here $a_n$, $L$, and $\epsilon$ are real numbers, $n,n_0\in\nnn$.) Alternative notation: $a_n\to L$.

11.19 HW (4 points) Give an analogous definition for the statement $\lim_{n\to\infty} a_n = \infty$. Specify the universe for each variable.

11.20 HW (3 points) Find a sequence $(c_n\mid n\in\nnn)$ such that $c_n \to \infty$ but $(\forall k)(c_{2k+1} < c_{2k})$ .

11.21 DEF (asymptotic equality)   Let $(a_n)$, $(b_n)$ be eventually non-zero sequences of real numbers (Def 11.17). We write that $a_n\sim b_n$ and say that the sequence $(a_n)$ is asymptotically equal to the sequence $(b_n)$ if $$ \lim_{n\to\infty} \frac{a_n}{b_n} = 1. $$ The LaTeX for $a_n\sim b_n$ is   $\texttt{\$a_n \sim b_n\$}$

11.22 HW (4 points) Prove that asymptotic equality is an equivalence relation among eventually non-zero sequences.

11.23 Note: no sequence is asymptotically equal to the all-zero sequence $(0,0,0,\dots)$. Not even itself.

11.24 DO   (a) $n^2+n \sim n^2$.   (b) $3z^7+10z^6-10^{10^{10}}z^4+8z^2-73z+89 \sim 3z^7$   (c) More generally, every polynomial is asymptotically equal to its leading term: if $f(x)=c_kx^k+c_{k-1}x^{k-1}+\dots + c_1x+c_0$ where $c_k\neq 0$ then $f(x)\sim c_k x^k$.

11.25 DO   If $a_n\sim b_n$ and $x_n\sim y_n$ then $a_n x_n \sim b_n y_n$ and $a_n/x_n \sim b_n/y_n$.

11.26 HW (2+5 points, due Tuesday) (a) Prove: $\lim_{n\to\infty} (\sqrt{n+1}-\sqrt{n}) = 0$.   (b) Prove: there exist real numbers $a,b$ such that $\sqrt{n+1}-\sqrt{n} \sim an^b$.   Find $a,b$.

11.27 HW (Bonus, 5 points, due Tuesday) True or false: If $a_n, b_n, x_n, y_n > 0$ and $a_n\sim b_n$ and $x_n\sim y_n$ then $a_n+x_n \sim b_n+y_n$. Give a clear answer and prove it.

11.28 DO   If $a_n, b_n > 0$ and $a_n\sim b_n$ then $\sqrt{a_n} \sim \sqrt{b_n}$.

11.29 HW (4 points) Find sequences $a_n, b_n$ such that $a_n, b_n \to \infty$ and $a_n\sim b_n$ but $2^{a_n} \not\sim 2^{b_n}$.

11.30 HW (4+6 points, due Tuesday) Let $a_n, b_n > 1$. Consider the following statement: $a_n \sim b_n \implies \ln a_n \sim \ln b_n$.
(a) Prove that this statement is false.   (b) Prove that the statement becomes true if we assume that $a_n$ and $b_n$ are bounded away from 1, i.e., $(\exists c > 0)(a_n, b_n > 1+c_n)$.

11.31 Notation: prime counting function.   Let $\pi(x)$ denote the number of primes $\le x$. For instance, $\pi(10)=4$, $\pi(100)=25$, $\pi(1)=0$, $\pi(\pi)=2$ (verify!).

11.32 PRIME NUMBER THEOREM (Jacques Hadamard and Charles de la Vallée Poussin, 1896) $$ \pi(x) \sim \frac{x}{\ln x} $$

11.33 DO   The PNT can be equivalently restated as follows.   Let us pick an integer $k$ at random from $[x]$. Then the probability that $k$ is prime is $$ \frac{\pi(x)}{x} \sim \frac{1}{\ln x} $$ (We are using the naive notion of probability: number of good cases divided by the number of all cases.)

11.34 HW (3 points) Estimate the probability that a random $100$-digit integer is prime. We permit leading zeros, so more precisely we are picking a positive integer with at most 100 digits (in decimal). Give your estimate in the form $1/N$ where $N$ is an integer. Assume that $10^{100}$ is large enough for the Prime Number Theorem to give a good approximation.

11.35 HW (3 points) Prove: there exist real numbers $a,b$ such that $\binom{n}{5} \sim a n^b$. Find $a,b$.

11.36 Stirling's formula   $\displaystyle{n! \sim \left(\frac{n}{\eee}\right)^n\sqrt{2\pi n}}$

11.37 HW (5 points, due Tuesday) Prove: there exist real numbers $a,b,c$ such that $\binom{2n}{n}\sim a n^b c^n$. Find $a,b,c$. Use Stirling's formula.

Class 10, Thu 10-31  
Median. All modules in $\zzz$ are cyclic -- proof. Applications: Greatest common divisor of a set of numbers, least common multiple of a set. Counting.
The homework problems are due Tuesday, November 5, including 9.1B, 9.5, 9.17, 9.21B, 9.26.

REMINDER. The default for each problem is that you have to prove your answer. The only exceptions are those where it is expressly stated that proof is not required.

10.1 HW ((2+2)+4+3+4B points) The median of an odd number of real numbers is the number in the middle: if the numbers are $a_0 \le a_1 \le \dots \le a_{2k}$ then their median is $a_k$. If the numbers are not given in increasing order, we first sort them. For instance, MEDIAN$(3, 5, 3, 9, 5) =$ MEDIAN$(3, 3, {\mathbf{5}}, 5, 9)= 5$.
Let us consider a class of $n=2k+1$ students who are graded on two sets of assignments. (E.g., ordinary and bonus problems.) Student $S_i$ gets $a_i$ points on the first set of assignments and $b_i$ points on the second; these are nonnegative real numbers. The total score of student $S_i$ is $c_i := a_i + b_i$. Let MEDIAN$(a_1,\dots,a_n)=A$, MEDIAN$(b_1,\dots,b_n)=B$, MEDIAN$(c_1,\dots,c_n)=C$. Assume $A,B > 0$.
(a1) Give an example with $n=5$ where $C > A+B$ and (a2) another example with $n=5$ where $C < A+B$.
(b) Prove:   $A+B\le 2C$.
(c) Prove that the inequality $A+B\le 2C$ is tight for every odd $n\ge 3$.
(d) (Bonus) Determine $\sup \frac{C}{A+B}$ where the supremum is taken over all sets of data with a fixed odd number $n\ge 3$ of students.

10.2 DO   Review the definition of greatest common divisor of a pair of integers. (It is not necessarily greatest by magnitude!)

10.3 DEF (greatest common divisor of a set of numbers)   Let $S\subseteq\zzz$. We say that $d$ is a greatest common divisor of $S$ if
(i) $d$ is a common divisor, i.e., $(\forall x)(x\in S \implies d\mid x)$
(ii) $d$ is a common multiple of all common divisors, i.e., $(\forall e)((\forall x)(x\in S\implies e\mid x)\implies e\mid d)$
Note that the statement in the middle, $$(\forall x)(x\in S\implies e\mid x)$$ means that $e$ is a common divisor of the elements of $S$.

10.4a NOTATION   Let $\Div(S)$ denote the set of common divisors of $S$. So $(\forall e)(e\in\Div(S) \iff (\forall x)(x\in S \implies e\mid x)).$

10.4b DO   How does this notation fit with our earlier notation $\Div(a)$ for the set of divisors of the number $a$ and $\Div(a,b) = \Div(a)\cap \Div(b)$ for the set of common divisors of $a$ and $b$? Verify that $\Div(a)=\Div(\{a\})$ and $\Div(a,b)=\Div(\{a,b\})$ where on the left-hand side we use the old notation and on the right-hand side we use the new notation. This means there is no conflict between the two notations, and we can continue to use both.

10.5 DO   Verify that $d$ is a greatest common divisor of the set $S$ if and only if
(i)   $d\in \Div(S)$
(ii)   $(\forall e)(e\in\Div(S) \implies e\mid d)$

10.6 HW (3+4 points) (a) Determine $\Div(\zzz)$.   (b) Determine $\Div(\emptyset)$.

10.7 DO   Let $R\subseteq S\subseteq \zzz$. Prove: $\Div(R) \supseteq \Div(S)$

10.8 DO   Let $R,S\subseteq\zzz$. Prove: $\Div(R\cup S) = \Div(R)\cap\Div(S)$

10.9 HW (3 points) Give an example of two sets $R,S\subseteq\zzz$ such that $\Div(R\cap S)\neq \Div(R)\cup \Div(S)$. Make $|R|+|S|$ as small as possible.

10.10 DO   Prove: $d$ is a greatest common divisor of $S$ if and only if $\Div(S) = \Div(d)$.

10.11a DEF   For $S\subseteq \zzz$, a finite linear combination of $S$ is a linear combination of a finite subset of $S$. For instance, if $P$ is the set of prime numbers then for all values $x,y,z\in \zzz$, the number $5x + 13y + 29z$ is a finite linear combination of $P$.

10.11b NOTATION   $\zzz[S]$ denotes the set of all finite linear combination of $S$ (with integer coefficients).

10.11c DO   $0$ is always a member of $\zzz[S]$, even if $S$ is the empty set. (Why?)

10.12 DO   Let $S\subseteq \zzz$. Prove: if $d\in\Div(S)$ and $d\in \zzz[S]$ then $d$ is a greatest common divisor of $S$.

10.13 COMMENT   We shall study the existence and uniqueness of greatest common divisors. We start with the easier question: uniqueness.

10.14 DO (gr.c.d. unique up to sign) Prove: if $d$ is a greatest common divisor of $S$ then a number $x$ is a greatest common divisor of $S$ if and only if $x =\pm d$.

10.15 NOTATION (gcd) If $d$ is a greatest common divisor of $S$ then we write $\gcd(S)=|d|$. According to the preceding exercise, $\gcd(S)$ is unique.

10.16 COMMENT   Next we show the existence of a greatest common divisor. Simultaneously, we also prove the generalization of Bézout's Lemma for sets of numbers. We use Ex. 8.43 (every module in $\zzz$ is cyclic). Review DEF 8.42 (module).

10.17 DO   Prove: for all $S\subseteq\zzz$, the set $\zzz[S]$ is a module.

10.18 DO   Prove the following.
THEOREM (existence of greatest common divisor and Bézout's Lemma).
Every set $S\subseteq\zzz$ has a greatest common divisor and this greatest common divisor is a finite linear combination of $S$.
Hint. 10.17 says $\zzz[S]$ is a module. So, by Theorem 8.43, $\zzz[S]$ is a cyclic module, i.e., $(\exists k)(\zzz[S]=k\zzz$. This $k$ is our suspect. Use Ex. 10.12 to show that $k$ is indeed a greatest common divisor of $S$.

10.19 HW (2+4 points) Determine (a) $\gcd(\zzz)$   (b) $\gcd(\emptyset)$.

10.20 HW (7 points) Let $R=\{p^2-1 \mid p\text{ is a prime number and } p\ge 19\}$. Determine $\gcd(R)$.

10.21 DEF (least common multiple of a set of numbers)   Let $S\subseteq \zzz$. We say that $m$ is a least common multiple of $S$ if
(i) $m$ is a common multiple, i.e., $(\forall x)(x\in S \implies x\mid m)$
(ii) $m$ is a common divisor of all common multiples, i.e., $(\forall n)((\forall x)(x\in S\implies x\mid n)\implies m\mid n)$
Note that the statement in the middle, $$(\forall x)(x\in S\implies x\mid n)$$ means that $n$ is a common multiple of the elements of $S$.

10.22 NOTE that this definition is the dual of DEF 10.3: we switch the two sides of each divisibility relation in the definition (divisor becomes multiple and vice versa).

10.23 DO (uniqueness up to sign) Prove: if $m$ is a least common common multiple of $S$ then a number $y$ is a least common multiple of $S$ if and only if $y = \pm m$.

10.24 NOTATION (lcm) If $m$ is a least common multiple of $S$ then we write $\lcm(S)=|m|$. According to the preceding exercise, $\lcm(S)$ is unique.

10.25 DO   Prove: the set of common multiples of $S$ is the set $$ \bigcap_{a\in S} a\zzz\,.$$ For the case $S=\emptyset$, reconcile your answer with DEF 10.26.

10.26 DEF (empty intersection) To make sense of problem 10.25 for the case when $S=\emptyset$, we need to define the intersection of an empty family of sets. The fewer sets we intersect, the bigger the intersection; this suggests that the empty intersection should be the biggest of all. This requires that we specify a universe (the biggest set of all that we consider); in our case, the universe is $\zzz$. So for an empty family of subsets of $\zzz$ we define their intersection $\bigcap_{R\in\emptyset} R :=\zzz$. In general, the empty intersection will be the universe specified.

10.27 HW (5 points) Let $I$ be a set and for $i\in I$, let $M_i\subseteq \zzz$ be a module. Prove: $$ \bigcap_{i\in I} M_i $$ is a module.

10.28 DO (existence of lcm) Prove: every set $S\subseteq \zzz$ has a least common multiple.
Hint. According to 10.25, the set of common multiples is the intersection of the cyclic modules $a\zzz$ where $a\in S$. So this set itself is a module according to 20.27. But then it is cyclic, so there exists $\ell$ such that the set of common multiples of $S$ is $\ell\zzz$. This $\ell$ is our suspect. Verify that $\ell$ is indeed a least common multiple of $S$.

10.29 HW (3+4 points) Determine (a) $\lcm(\zzz)$   (b) $\lcm(\emptyset)$.

10.30 Bonus (4 points) Determine, which sets $S\subseteq\zzz$ satisfy $\lcm(S)=0$. Give a very simple characterization.

10.31 HW (5 points) Consider the system of simultaneous congruences described in Def. 8.28. Prove: if the system is feasible then the set of solutions is a residue class modulo $L$ where $L = \lcm(m_1,\dots,m_k)$.   In other words, if $x_0$ is a solution to the system then a number $y$ is a solution if and only if $y\equiv x_0 \pmod L$.   In particular, the solution is unique modulo $L$.

10.32 DO   Let $m_1,\dots, m_k > 0$. Prove: $\lcm(m_1,\dots,m_k)=\prod_{i=1}^k m_i$ if and only if the $m_i$ are pairwise relatively prime.

10.33 HW (4 points) Show that the preceding exercise becomes false if we replace the condition $m_1,\dots, m_k > 0$ by $m_1,\dots, m_k\ge 0$. Give a counterexample that has no repeated moduli (i.e., $m_i=m_j \implies i=j$). Give the smallest counterexample: make $\sum_{i=1}^k m_i$ as small as possible.

10.34 DO   (Computing gcd and lcm given the prime factorization)   Let $a,b$ be positive integers with prime factorizations $a=p_1^{k_1}\dots p_s^{k_s}$ and $a=p_1^{\ell_1}\dots p_s^{\ell_s}$ where $k_i, \ell_i \ge 0$. Then $\gcd(a,b)=\prod_{i=1}^s p_i^{\min(k_i,\ell_i)}$ and $\lcm(a,b)=\prod_{i=1}^s p_i^{\max(k_i,\ell_i)}\,$.
Example. Let $a=72$ and $b=300$. Then $a=2^3\cdot 3^2\cdot 5^0$ and $b=2^2\cdot 3\cdot 5^2$. Therefore $\gcd(a,b)=2^2\cdot 3\cdot 5^0 = 12$ and $\lcm(a,b)=2^3\cdot 3^2\cdot 5^2=1800$.

10.35 HW (5 points, due Thursday) Prove: if $a,b\in\zzz$ then $\gcd(a,b)\cdot \lcm(a,b)=|a|\cdot|b|$.   Use the preceding exercise. State a simple lemma relating the min and max functions.

10.36 STUDY the standard deck of 52 cards. They come in four suits called spades $\spadesuit$, clubs $\clubsuit$, hearts $\heartsuit$, and diamonds $\diamondsuit$. They come in 13 kinds, 2-10 and Jack, Queen, King, and Ace. So there is a card designated $7\clubsuit$ (7 of clubs) and another designed $Q\diamondsuit$ (Queen of diamonds). A poker hand is a set of 5 cards, so there are $\binom{52}{5}$ poker hands. (The orderx of the cards does not matter.) Various types of poker hands have names. For instance, a poker hand is called "4 of a kind" if it includes four cards of the same kind, for instance $K\diamondsuit$, $5\clubsuit$, $K\spadesuit$, $K\heartsuit$, $K\clubsuit$. A hand is a full house if it includes 3 of a kind and two of another kind, for instance $6\spadesuit$, $A\heartsuit$, $6\clubsuit$, $6\diamondsuit$, $A\spadesuit$.

10.37 DO   What is the probability that a random poker hand is 4 of a kind?   Give your answer as a rational number in canonical form (prime factorization). Show all your work. Do not use electronic devices or any calculation with numbers that have more than two digits.
Use the naive notion of probability: number of good cases divided by the number of all cases.
Solution. The number of all cases (the denominator) is $\binom{52}{5}$. We calculate the number of "good cases." There are 13 choices for what kind of card appears 4 times $13$. The fifth card is any of the remaining $4\cdot 12$ cards, so the total is $13\cdot 12\cdot 4$. The result is $$\frac{13\cdot 12\cdot 4}{\binom{52}{5}} = \frac{13\cdot 12\cdot 4\cdot 5\cdot 4\cdot 3\cdot 2} {52\cdot 51\cdot 50 \cdot 49 \cdot 48} = \frac{13\cdot 4}{52}\cdot \frac{12\cdot 4}{48} \cdot \frac{5\cdot 2}{50} \cdot\frac{3}{51}\cdot\frac{1}{49} = \frac{1}{5}\cdot \frac{1}{17}\cdot\frac{1}{49} = 5^{-1}\cdot 7^{-2}\cdot 17^{-1}.$$

10.38 HW (5+5 points, due Thursday)   What is the probability that a random poker hand (a) is a full house (b) has no two cards of the same kind?   Give your answers as rational numbers in canonical form (prime factorization). SHOW ALL YOUR WORK. Do not use electronic devices or any calculation with numbers that have more than two digits.
Use the naive notion of probability: number of good cases divided by the number of all cases.

Class 9, Tue 10-29  
Linear congruences. Counting permutations with repeated items. Multinomial coefficients. Binomial coefficients. Binomial Theorem. Identities for binomial coefficients, combinatorial and algebraic proofs.
The homework problems due Thursday, October 30, are   8.43 (Bonus), 9.9, 9.20.

9.1 Bonus (9 points, due Tuesday) Let $m\ge 1$. Prove that the Fibonacci numbers modulo $m$ are periodic, and the period is $\le m^2-1$. In other words, prove that $(\forall m\ge 1)(\exists k)(1\le k\le m^2-1\text{ and } (\forall i\ge 0)(F_i\equiv F_{i+k} \pmod m)$

9.2 DO   The linear congruence $9x\equiv 7 \pmod{21}$ has no solution. Here $x$ is a symbol for an unknown.
Proof by contradiction. Assume $x_0$ is a solution, so $x_0\in\zzz$ and $9x_0\equiv 7 \pmod{21}$. By Ex. 8.26, we infer that $9x_0\equiv 7 \pmod{3}$. But $9$ is divisible by $3$, so $9x_0\equiv 0 \pmod{3}$. By the transitivity of congruence mod $3$ it follows that $0\equiv 7 \pmod 3$, i.e., $3\mid 7$, which is false. This contradiction proves that our assumption that $(\exists x_0)$ was false, proving that there is no solution. QED

9.3 DO   Consider the linear congruence $ax\equiv b\pmod m$. Prove: If $\gcd(a,m) \nmid b$ then the congruence has no solution.
Hint. Follow the steps of the proof in the preceding exercise.

9.4 THEOREM   The congruence $ax\equiv b\pmod m$ has a solution if and only if $\gcd(a,m) \mid b$.

Note that the "only if" part (necessity) is the content of Ex. 9.3. The "if" part (sufficiency) is the next exercise.

9.5 HW (6 points, due Tuesday)   Consider the linear congruence $ax\equiv b\pmod m$. Prove: If $\gcd(a,m) \mid b$ then the congruence is feasible (has a solution).    Hint. Bézout.

9.6 DEF   We say that the integer $b$ is a multiplicative inverse of the integer $a$ modulo $m$ if $ab\equiv 1 \pmod m$. We denote the smallest non-negative multiplicative inverse of $a$ by $(a^{-1} \bmod m)$.   For instance, $13$ is a multiplicative inverse of $7$ modulo $10$ because $7\cdot 13 = 91 \equiv 1 \pmod{10}$. But $13$ is not the smallest; $(7^{-1} \bmod{10})=3$.

9.7 DO   Let $a,m\in \zzz$. (a) Then $a$ has a multiplicative inverse modulo $m$ if and only if $a$ and $m$ are relatively prime.
(b) The multiplicative inverse is unique modulo $m$. In fact, if $b$ is a multiplicative inverse of $a$ modulo $m$ then $(\forall c)((c\text{ is a multiplicative inverse of }a \bmod m) \iff c\equiv b\pmod m)$. In other words, the set of multiplicative inverses of $a$ is a residue class modulo $m$.
Hint for part (a). This follows immediately from Theorem 9.4.

9.8 DO   Find $(29^{-1} \bmod{37})$.
Solution. We need to solve the congruence $29x\equiv 1\pmod{37}$ and find the solution in the interval $1\le x\le 36$. We note that a solution exists because $\gcd(29,37)=1$. We start with this pair of congruences: $$\begin{align*} (1)&\quad& 37x &\equiv 0 \pmod{37}\\ (2)&\quad& 29x &\equiv 1 \pmod{37} \end{align*} $$

Then we apply Euclid's algorithm to the coefficient of $x$ until the coefficient becomes 1.
$$\begin{align*} (3)&\quad& 8x &\equiv -1 & \pmod{37} & \quad & \text{subtracted Eq (2) from Eq (1)}\\ (4)&\quad& 24x &\equiv -3 & \pmod{37} & \quad & \text{multiplied Eq (3) by 3}\\ (5)&\quad& 5x &\equiv 4 & \pmod{37} & \quad & \text{subtracted Eq (4) from Eq (2)}\\ (6)&\quad& 3x &\equiv -5 & \pmod{37} & \quad & \text{subtracted Eq (5) from Eq (3)}\\ (7)&\quad& 2x &\equiv 9 & \pmod{37} & \quad & \text{subtracted Eq (6) from Eq (5)}\\ (8)&\quad& x &\equiv -14 & \pmod{37} & \quad & \text{subtracted Eq (7) from Eq (6)}\\ \end{align*} $$

The conclusion is that if a solution exists, it must be $x\equiv -14\pmod{37}$ and therefore $x=23$. Since we know that a solution exists, and this is the only possibility, it follows that this is the solution. Checking is therefore not mandatory, but recommended in case an arithmetic error was made.
Checking: We need to verify that $23\cdot 29\equiv 1 \pmod{37}$. Noting that $23\equiv -14\pmod{37}$ and $29\equiv -8\pmod{37}$, we need to verify that $8\cdot 14\equiv 1 \pmod{37}$, i.e., $37 \mid 8\cdot 14 -1 = 111 = 3\cdot 37$.

Faster solution. We can speed up the procedure if we follow the spirit but not the letter of Euclid's algorithm, always choosing the linear combination that leads to the smallest coefficient. After Eq (3) continue as follows.
$$\begin{align*} (4')&\quad& 32x &\equiv -4 & \pmod{37} & \quad & \text{multiplied Eq (3) by 4}\\ (5')&\quad& 3x &\equiv -5 & \pmod{37} & \quad & \text{subtracted Eq (2) from Eq (4')}\\ (6')&\quad& 9x &\equiv -15 & \pmod{37} & \quad & \text{multiplied Eq (5') by 3}\\ (7')&\quad& x &\equiv -14 & \pmod{37} & \quad & \text{subtracted Eq (3) from Eq (6')}\\ \end{align*} $$
The first solution used 5 rounds of the while loop, the second made only three analogous rounds.

HW 9.9 (6 points) Solve the linear congruence $$18x\equiv 1 \pmod{79}$$ using the method discussed in class (applying Euclid's algorithm or variants of it to the coefficient of $x$). Your final answer should be a number $0\le x\le 78$. SHOW ALL YOUR WORK (each step you take in executing the algorithm). In each step you get a new congruence of the form $bx\equiv c \pmod{79}$ (the modulus never changes, the coefficients $b$ and $c$ change at each step). Number your equations and annotate your steps. Typical annotations would sound like this: "multiply Eq. (3) by (-5)," or "subtract Eq. (5) from Eq. (3)."

9.10 Counting equivalence classes: King Matthias' shepherd's principle.
The good King Matthias liked to demonstrate to his entourage of noblemen how smart his common people were. One day, walking in the pastures, he encountered a shepherd. The King asked if the shepherd knew how many sheep were in his herd. The shepherd bowed down, looked under his sheep's belly, then rose and answered "343, Sire." "How did you count them?" "Very simple, Sire. I just counted their legs, and then divided the number by 4."
The shepherd noticed that there was a natural equivalence relation on the set of legs: two legs are equivalent if they belong to the same sheep. His job was to count the equivalence classes. This was made possible by the fact that each equivalence class had the same size (four).
The general principle: If a set of $n$ elements is divided up into $k$ equivalence classes and each equivalence class has $N$ elements then $k=n/N$.

This simple observation is a remarkably useful counting tool.

9.11 Counting permutations with repeated elements. What is the number of strings of length 10 over the alphabet $\{A,B,C\}$ containing the letter $A$ 3 times, the letter $B$ twice, and the letter $C$ 5 times?
Solution. The set of 10 positions has $10!$ permutations. Let us apply these permutations to the string $s = AAABBCCCCC$. For instance, the permutation $\pi=(1\to 5, 2\to 2, 3\to 10, 4\to 8, 5\to 6, 6\to 1, 7\to 7, 8\to 4, 9\to 3, 10\to 9$ applied to $s$ produces the string $\pi(s) = CACCABCBCA$. Let us say that two permutations of the positions are equivalent if they result in the same string. Given a permutation $\pi$, we get the permutations equivalent to $\pi$ by first applying any permutation $\tau$ that does not change any letter, and then applying $\pi$. The number of such permutations $\tau$ is $3!2!5!$ (DO: why?), so this is the size of each equivalence class. Therefore the number in question is $\displaystyle\frac{10!}{3!2!5!}= \frac{10\cdot 9\cdot 8\cdot 7\cdot 6}{3!2!}= 10\cdot 9\cdot 4\cdot 7 = 2520$.

9.12 THEOREM. Let $n=k_1+\dots+k_s$ where $k_i\ge 0$. Let $\binom{n}{k_1,\dots,k_s}$ denote the number of strings of length $n$ over the alphabet $\{A_1,\dots,A_s\}$ where the multiplicity (number of occurrences) of $A_i$ is $k_i$. Then $$ \binom{n}{k_1,\dots,k_s} = \frac{n!}{\prod_{i=1}^s k_i!}\,.$$ This number is called a multinomial coefficient. DO: Prove this theorem using King Matthias' shepherd's principle.

9.13 TERMINOLOGY.   An $n$-set is a set of $n$ elements. A $k$-subset of a set $A$ is a $k$-set that is a subset of $A$.

9.14 DEF   Let $n,k\ge 0$. The binomial coefficient $\binom{n}{k}$ is the number of $k$-subsets of an $n$-set.

9.15 DO   (a) If $k > n$ then $\binom{n}{k}=0$.   (b) $\binom{n}{0}=\binom{n}{n}=1$. (c) If $0\le k\le n$ then $\binom{n}{k} = \binom{n}{n-k}$. (Give a bijective proof of (c).}

9.16 DO   (a) If $0\le k\le n$ then $$ \binom{n}{k} = \binom{n}{k,n-k} = \frac{n!}{k!(n-k)!} = \frac{n(n-1)\cdots (n-k+1)}{k!} \,.$$ Hint. Bijection between the set of $k$-subsets of an $n$-set and the strings of length $n$ consisting of $k$ copies of $A$ and $(n-k)$ copies of $B$. (b) For all $n,k \ge 0$ we have $$ \binom{n}{k} = \frac{n!}{k!(n-k)!} = \frac{n(n-1)\cdots (n-k+1)}{k!} \,.$$ (What you need to show is that this equality remains valid even is $k > n$.) In particular, $$\binom{n}{2}=\frac{n(n-1)}{2}, \quad \binom{n}{3}=\frac{n(n-1)(n-2)}{3}\,.$$

9.17 HW (Pascal's Identity, 4 points, due Tuesday) For $0\le k\le n$ prove: $$ \binom{n+1}{k+1} = \binom{n}{k+1} + \binom{n}{k}\,.$$ Give a bijective proof. Do not use the formula involving factorials.

9.18 DO   Use 9.15(b) and Pascal's identity to build Pascal's triangle, the infinite triangle consisting of the values of the binomial coefficients, with the $n$-th row being the sequence $\binom{n}{0}$, $\binom{n}{1},\dots, \binom{n}{n}$. Write down rows number $0,1,\dots,8.$

9.19 ART PROJECT   Write down the first 30 rows of the Pascal triangle mod 2. (All entries will be 0 or 1.) Observe the pattern.

HW 9.20 (6 points) Let $n\ge k\ge 0$. Prove the following identity by induction on $n$. $$ \sum_{s=k}^n \binom{s}{k} = \binom{n+1}{k+1}\,.$$ Use Pascal's identity and the fact that $(\forall m\ge 0)(\binom{m}{0}=\binom{m}{m}=1)$. &nbap; Do NOT use the explicit form of the binomial coefficients using factorials.   Note that you have to prove this for every $k$. For each $k$ you will have a different base case. Given $k$, what is the base case (smallest value of $n$ you have to consider)?

Bonus 9.21 (5 points, due Tuesday) Let $A\subseteq \zzz$ be an $n$-set. (a) Prove: $|A+A+A| \le \binom{n+2}{3}.$   (b) Prove that this upper bound is tight for every $n$.

9.22 DO   Note: $|A|=n=\binom{n}{1}$ and we have seen that $|A+A|\le \binom{n+1}{2}$. Detect any pattern? Guess the maximum size of $|A+A+A+A|$.

9.23 Binomial Theorem $$(x+y)^n = \sum_{k=0}^n \binom{n}{k} x^k y^{n-k}\,.$$ (To be proved later.) Example: $$ (x+y)^5 = x^5 + 5x^4y + 10x^3y^2 + 10 x^2y^3 + 5xy^4 + y^5\,$$

9.24 DO   Prove the following identity. $$ \sum_{k=0}^n \binom{n}{k} = 2^n\,. $$ Give (a) a combinatorial proof (counting subsets in two ways) and (b) an algebraic proof (use the Binomial Theorem). (Hint for (b): set $x=y=1$.)

9.25 DO   The number of even subsets of an $n$-set is $$ E_n=\binom{n}{0}+\binom{n}{2}+\binom{n}{4}+\dots$$ and the number of odd subsets is $$ O_n=\binom{n}{1}+\binom{n}{3}+\binom{n}{5}+\dots\,.$$ We have seen a combinatorial proof of the identity $E_n = O_n$ for $n\ge 1$. Give an algebraic proof.   Hint: $E_n-O_n = (1-1)^n$. (Why?) The right-hand side is $0$ for $n\ge 1$ but note also that for $n=0$ the right-hand side correctly evaluates to 1.

9.26 HW (3 points, due Tuesday) Evaluate the following expression. $$ \sum_{k=0}^{\infty} \binom{n}{k} (1/2)^k \,.$$ Your answer should be a very short formula (six symbols only). The proof should be less than one line: just state what case of the Binomial Theorem you are using, and state why this seemingly infinite sum is actually finite.

Class 8, Thu 10-24  
Cancellation law, complete set of residues, proof of Fermat's little Theorem, applications, splitting a congruence with composite modulus, system of simultaneous congruences, feasibility, Chinese Remainder Theorem, necessary vs. sufficient condition, module in $\zzz$, cyclic module, elegant alternative proof of the existence of a $\gcd$ and of Bézout's Lemma.
Homework due Tuesday, October 29. Remember that two Bonus problems assigned last Tuesday are also due 10-29 (7.7B, 7.8B).

8.1 DO REVIEW the definition of gcd (3.4 DEF). It is NOT the greatest in magnitude among the common divisors.

8.2 DO   Prove: If $a\mid bc$ and $\gcd(a,b)=1$ then $a\mid c$. Do not use the Fundamental Theorem of Arithmetic, just basic facts about the gcd.   Note: this is a special case of Exercise 6.16. Review the proof. (It uses Bézout's Lemma.)

8.3 HW (3 points) Prove: If $\gcd(a,b)=1$ then $\gcd(a,bc)=\gcd(a,c)$.   Use Exercise 8.2 to prove, in one line, that $\gcd(a,bc)\mid\gcd(a,c)$. Use only the definition of $\gcd$ (3.4 DEF) to prove that $\gcd(a,c)\mid\gcd(a,bc)$.

8.4 HW (4 points) Use Exercise 8.2 to prove: If $r,s\mid a$ and $\gcd(r,s)=1$ then $rs\mid a$.   (2 lines.) Do not use the Fundamental Theorem of Arithmetic.

  Hint. Solve the case $r=0$. If $r\neq 0$, use Ex. 8.2 to prove that $s\mid a/r$.

8.5 HW (2 points) (Cancellation law) Prove: If $ac\equiv bc \pmod m$ and $\gcd(c,m)=1$ then $a\equiv b \pmod m$.   (2 lines) State which previous exercise you are using.

8.6 HW (3 points) Prove: If $c\mid a$ and $c\mid b$ and $c\mid m$ and $c\neq 0$ then the following two statements are equivalent:
1.   $a\equiv b \pmod m$
2.   $a/c \equiv b/c \pmod{(m/c)}$

8.7 Bonus (4 points) Prove: If $c\mid a$ and $c\mid b$ and $c\neq 0$ and $a\equiv b \pmod m$ then $a/c\equiv b/c\pmod{(m/d)}$ where $d=\gcd(c,m)$.   (2 lines) Use Ex. 6.16.

8.8 HW (3 points) (splitting composite modulus) Let $m=rs$. Assume $\gcd(r,s)=1$. Prove that the following two statements are equivalent.
(a)   $a\equiv b \pmod m$
(b)   $a\equiv b \pmod r$ and $a\equiv b \pmod s$.
(2 lines) Use a previous exercise.

8.9 DEF (recall) A complete set of residues modulo $m$ is a set of integers that includes eactly one number from each residue class mod $m$.

8.10 DO   Let $m\ge 1$. Prove: a set $R$ of integers is a complete set of residues mod $m$ if and only if $|R|=m$ and the elements of $R$ are pairwise not congruent mod $m$.

8.11 HW (4 points) Let $m\ge 1$. Prove: if $\{r_0,\dots,r_{m-1}\}$ is a complete set of residues mod $m$ and $\gcd(a,m)=1$ then $\{ar_0,\dots,ar_{m-1}\}$ is also a complete set of residues mod $m$.

8.12 DO   Prove that the condition $\gcd(a,m)=1$ is not only sufficient but also necessary for the conclusion of the preceding exercise to hold. In other words, show that if $\gcd(a,m)\neq 1$ then $\{ar_0,\dots,ar_{m-1}\}$ is not a complete set of residues mod $m$.

8.13 Fermat's little Theorem (FlT) Let $p$ be a prime. Then $(\forall a)(a^p\equiv a \pmod p)$.

8.14 (FlT version 2) Let $p$ be a prime. If $\gcd(a,p)=1$ then $a^{p-1}\equiv 1 \pmod p$.

8.15 HW (4 points) Prove that the two versions of FlT are equivalent (each version follows from the other).

8.16 DO   Let $p$ be a prime. Prove: $\gcd(p, (p-1)!)=1$.

8.17 Proof of FlT version 2.   The numbers $0,1,2,\dots,p-1$ form a complete set of residues mod $p$. Therefore $0\cdot a, 1\cdot a, 2\cdot a,\dots, (p-1)\cdot a$ also form a complete set of residues mod $p$ (because $\gcd(a,p)=1$). Now $0 = 0\cdot a$, so the remaining $p-1$ members of each complete set of residues correspond to each other: there is a bijection $f: \{1,2,\dots,p-1\}\to \{1\cdot a,2\cdot a,\dots,(p-1)\cdot a\}$ such that $i \equiv f(i) \pmod p$. Therefore $\prod_{i=1}^{p-1} i \equiv \prod_{i=1}^{p-1} (ai) \pmod p$. In other words, $(p-1)! \equiv a^{p-1} (p-1)! \pmod p$. But $p$ is relatively prime to $(p-1)!$, so by the Cancellation Law (Ex. 8.5) we have $a^{p-1}\equiv 1 \pmod p$, as desired. QED

8.18 HW (4 points) Let $p$ be a prime. Prove: If $k,\ell \ge 1$ and $k\equiv \ell \pmod{(p-1)}$ then $(\forall a)(a^k\equiv a^{\ell}\pmod p)$.
This fact is used in the justification of the RSA Public Key Cryptosystem.

8.19 DO   If $\gcd(a,p)=1$ then the conclusion of 8.18 remains valid for $k,\ell \ge 0$.

8.20 NOTATION   Let $m \ge 1$. We write $(a \bmod m)$ to denote the smallest nonnegative remainder of $a$ modulo $m$. In other words, if $a = qm+r$ where $0\le r < m$ then we write $r=(a \bmod m)$.

8.21 DO   If $r=(a\bmod m)$ then $a\equiv r \pmod m$ and $0\le r\le m-1$.

8.22 DO   Compute $(3^{10^{10}} \bmod {17})$ without using any electronic devices.   Hint: We need to find $(10^{10} \bmod{16})$. This number is $0$ (DO: why?), so by Ex. 8.19, the answer is $3^0 =1$.

8.23 DO   Compute $(3^{10^{10}} \bmod {37})$ without using any electronic devices.   Solution. We need to find the value $x=(10^{10} \bmod{36})$. Since $36=4\cdot 9$, by Ex. 8.8 we need to find $(10^{10} \bmod{4})$ and $(10^{10} \bmod{9})$.
Now $(10^{10} \bmod 4)=0$ because $4\mid 2^{10}\mid 10^{10}$ and $(10^{10} \bmod 9)=1$ because $10\equiv 1 \pmod 9$ and therefore $10^{10}\equiv 1 \pmod 9$. So $x\equiv 0\pmod 4$ and $x\equiv 1\pmod 9$ and $0\le x \le 36$. DO:   $x=28$.
Now we need to calculate $y=(3^{28} \bmod 37)$.
$3^{27} = (3^3)^9 = (27)^9 \equiv (-10)^9 \pmod{37}$. Further, $(-10)^9=-10^9 =-(10^3)^3 =-1000^3$. Noting that $37\cdot 27=999$ we see that $1000\equiv 1 \pmod{37}$, so $3^{27}\equiv -1\pmod{37}$. So the final answer to our question is $y\equiv 3^{28}=3\cdot 3^{27}\equiv -3 \pmod{37}\equiv 34 \pmod{37}$.

8.24 HW (6 points)   Compute $(5^{10^{10}} \bmod {29})$ without using any electronic devices.   Make your calculations as easy as possible, doable on a small piece of paper. Show all your work!

8.25 HW (9 points)   Prove:   $(\forall a)(a^{13}\equiv a\pmod{91})$

8.26 HW (2 points)   Prove: if $a\equiv b \pmod m$ and $d\mid m$ then $a\equiv b \pmod d$.   What property of divisibility can we use for a very simple (one-line) proof?

8.27 TERMINOLOGY   When talking about a congruence $a\equiv b\pmod m$, we refer to $a$ as the left-hand side, $b$ the right-hand side, and $m$ the modulus. The plural of "modulus" is moduli.

8.28 DEF (system of simultaneous congruences)  Let $a_1,\dots,a_k,m_1,\dots,m_k\in\zzz$. Consider the following list of congruences. $$\begin{align*} x &\equiv a_1 \pmod{m_1}\\ x &\equiv a_2 \pmod{m_2}\\ &\vdots\\ x &\equiv a_k \pmod{m_k} \end{align*} $$ Such a list is called a "system of simultaneous congruences." The numbers $m_1,\dots,m_k$ are the moduli of the system. Here $x$ is an "unknown," which is just a symbol. We say that a number $x_0\in\zzz$ satisfies this system if $x_0$ satisfies each of congruences on the list, i.e., $(\forall i)(x_0\equiv a_i \pmod{m_i})$. Such a value $x_0$ is called a solution of the system. We also say "$x=x_0$ is a solution." Often we write $x$ for $x_0$, confounding a symbol for an unknown with a number, but the meaning should be clear from the context.
We call the system feasible if it has a solution and infeasible if it has no solution.

8.30 EXAMPLE   Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv 4 & \pmod{15}\\ x &\equiv -5 & \pmod{21}\\ x &\equiv 9 & \pmod{35} \end{align*} $$ This system is feasible because $x=79$ is a solution. (DO verify!)

8.31 Bonus (7 points) Prove: the value $x\in\zzz$ is a solution of the system in the preceding example if and only if $x\equiv 79 \pmod{105}$. In other words, the set of solutions of the system is $105\zzz+79$. What is the relation of the number $105$ to the moduli in this example?

8.32 EXAMPLE   Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv 4 & \pmod{15}\\ x &\equiv -5 & \pmod{21}\\ x &\equiv 19 & \pmod{35} \end{align*} $$ Claim. This system is infeasible.
PROOF BY CONTRADICTION. We use Ex. 8.26. Suppose for a contradiction that there is a solution, call it $x_0$. The second congruence implies $x_0\equiv -5 \pmod 7$ (because $7\mid 21$). The third congruence implies $x_0\equiv 19 \pmod 7$ (because $7\mid 35$). By the symmetry and transitivity of congruence mod $7$ we infer that $-5 \equiv 19 \pmod 7$, which means $7\mid 24$, which is false. Our assumption that the system is feasible has led to the false conclusion $7\mid 24$, proving that our assumption was wrong. (In other words, this conclusion contradicts our assumption.) This contradiction proves the Claim. QED

8.33 HW (5 points)   Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv 103 & \pmod{8}\\ x &\equiv -7 & \pmod{55}\\ x &\equiv 13 & \pmod{20} \end{align*} $$ Prove that this system is infeasible.

8.34 CHINESE REMAINDER THEOREM (CRT) Consider the system of simultaneous congruences in Def. 8.28. If the moduli $m_i$ are pairwise relatively prime (i.e., $(\forall i\neq j)(\gcd(m_i,m_j)=1)$) then the system is feasible.

8.35 EXAMPLE. Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv a & \pmod{8}\\ x &\equiv b & \pmod{55}\\ x &\equiv c & \pmod{63} \end{align*} $$ CRT guarantees that this system is feasible regardless of the values $a,b,c\in\zzz$. (DO verify that the moduli are pairwise relatively prime, i.e., $\gcd(8,55)=\gcd(8,63)=\gcd(55,63)=1$.)

8.36 COMMENT.   CRT gives a sufficient condition of feasibility: the condition that the moduli are pairwise relatively prime suffices for feasibility. It is not a necessary condition of feasibility: a system can be feasible even if the moduli are not pairwise relatively prime. We have seen such a system in Example 8.30. The following exercise expands this observation.

8.37 HW (4 points) Prove: $(\forall m_1,\dots,m_k)(\exists a_1,\dots,a_k)$ such that the system of simultaneous congruences in Def. 8.28 is feasible.   Your solution should be one line.

8.38 HW (4 points) Find $m_1,m_2,a_1,a_2\in\zzz$ such that the pair $x\equiv a_i \pmod{m_i}$ $(i=1,2)$ of simultaneous congruences is infeasible and the following conditions are met: $m_1, m_2 >0$,  $m_2 \nmid m_1$,  $m_1 \nmid m_2$ (neither of the two moduli is a divisor of the other), and $m_1+m_2$ is as small as possible subject to these conditions. Prove (in one line) that your system is infeasible. No proof of minimality is required.

8.39 DEF   Let $M\subseteq \zzz$. We say that $M$ is a module if $M\neq \emptyset$ and $M$ is closed under substraction. The latter means that $(\forall a,b)(a,b\in M \implies a-b\in M)$.

8.40 DO   If $M$ is a module then $0\in M$.
Proof. Let $a\in M$. (How do we know such $a$ exists?) Then $a-a\in M$. QED

8.41 EXAMPLES   $\zzz$ and $\{0\}$ are modules. The set of even numbers, $2\zzz$, is a module. )The set of odd numbers is NOT a module! Why?) More generally, for any $k\in\zzz$, the set $k\zzz$ is a module. (DO: verify!)

8.42 DEF   A cyclic module is a module of the form $k\zzz$ for some $k\in\zzz$. For instance $\zzz$ itself is a cyclic module $(k=1)$, the zero module $\{0\}$ is also cyclic $(k=0)$, the set of even numbers is a cyclic module $(k=2)$.

8.43 Bonus (due Thursday) (9 points) Prove the following result.
THEOREM. Every module is cyclic.
In other words, if $M$ is a module then $(\exists k)(M=k\zzz)$.
Hint. (1) Prove: if $a\in M$ then $-a\in M$. (2) Prove that $M$ is closed under addition. (3) Prove: if $a\in M$ then $a\zzz\subseteq M$. (4) We need to find $k$ such that $M=k\zzz$. Give a simple definition of a suspect (a value $k$ that you believe satisfies $M=k\zzz$). Use the Division Theorem (Ex. 1.13 in the Euclid's algorithm handout) to prove that your suspect is guilty as charged, i.e., $M$ is indeed equal to $k\zzz$.

8.44 HW (1+3 points) Let $a,b\in\zzz$ and $M=a\zzz+b\zzz$. Prove: (a) $a,b\in M$   (b) $M$ is a module.

8.45 HW (6 points) Let $a,b\in\zzz$. Use the preceding two exercises to give a strikingly elegant alternative proof of the fact that $\gcd(a,b)$ exists and is representable as a linear combination of $a$ and $b$ (Bézout's Lemma).
So your proof cannot assume the existence of a gcd. Review the definition of a greatest common divisor (3.4 DEF).
Hint. Combine the preceding two exercises to find your suspect (a value $d$ which you believe should be a greatest common divisor of $a$ and $b$). Use Ex. 4.14 to prove that $d$ is guilty as charged ($d$ is a greatest common divisor of $a$ and $b$ and is a linear combination of $a$ and $b$).

8.46 Bonus (2+3+3 points) Let $a,b,c$ be integers. (a) Define what it means that the integer $d$ is a greatest common divisor of $a,b,c$. Model your definition after Def. 3.4. (b) Prove that such $d$ exists. (c) Prove that $d$ is a linear combination of $a,b,c$, i.e., $d$ can be written in the form $d=ax+by+cz$ (Bézout's Lemma). Model your proof of (b) and (c) after the preceding exercise. The entire proof should take no more than a few lines.

Class 7, Tue 10-22   Direct sum. Fundamental Theorem of Equivalence Relations. Congruences.
Homework due Thursday, October 24. Remember that several problems assigned last Thursday are also due 10-24.

7.1 DEF (Direct sum) Let $A,B \subseteq \zzz$. We say that the set $C\subseteq \zzz$ is the direct sum of $A$ and $B$ if $(\forall c\in C)(\exists ! a\in A, b\in B)(a+b=c)$. We denote this circumstance by $C=A\oplus B$.   (Recall that $\exists!$ means "there exists a unique." Here both $a$ and $b$ are required to be unique.)

7.2 COMMENT. Note the difference between $A+B$ and $A\oplus B$. The former consists of the elements that can be written as $a+b$ where $a\in A$ and $b\in B$; the latter makes the additional statement that this representation is unique. So while $A+B$ always exists, $A\oplus B$ does not necessarily exist. If $A\oplus B$ exists then $A\oplus B=A+B$.

7.3 DO Let $A,B\subseteq \zzz$. Prove: $A\oplus B$ exists if and only if the following holds. $(\forall a,a'\in A)(\forall b,b'\in B)(a+b=a'+b' \implies a=a' \text{ and } b=b')$.
For example, if $A=\{2,3\}$ and $B=\{5,6,8\}$ then the sum $A+B = \{7,8,9,10,11\}$ is not a direct sum because of the collision $2+6=3+5$.

7.4 DO Let $A,B$ be finite subsets of $\zzz$. Recall that $|A+B|\le |A|\cdot |B|$. Prove: $A\oplus B$ exists if and only if $|A+B|=|A|\cdot |B|$.
For example, if $A=\{2,3\}$ and $B=\{3,5,8\}$ then $A+B=\{5,6,7,8,10,11\}$ is a direct sum: $A+B=A\oplus B$ because there are no collisions of the type $a+b=a'+b'$, as witnessed by the fact that $|A+B|=6=|A|\cdot |B|$.

7.5 NOTATION   $\nnn = \{0,1,2,\dots\}$ denotes the set of non-negative integers.

7.6 HW (5 points) Find $A, B\subseteq\nnn$ such that $|A|=100$ and $A\oplus B=\nnn$. Give a simple and clear definition of the sets $A$ and $B$ (less than one line total). No proof required.

7.7 Bonus (5 points, due Tuesday) Find two infinite sets $A, B\subseteq\nnn$ such that $A\oplus B=\nnn$. Give a clear definition of the sets $A$ and $B$ (less than one line each). No proof required.

7.8 Bonus: triomino problem (5 points, due Tuesday) The problem is listed in the Puzzle problem sheet on the course home page (click "texts" on the banner). Your proof must be short and convincing. Find an invariant of all configurations tileable by trominoes; and show that your invariant fails for the region to be tiled.

7.9 HW (4 points) Prove by induction on $k$:   If $a\equiv b\pmod m$ then $(\forall k\ge 0)(a^k\equiv b^k \pmod m)$.

7.10 (Partitions vs. equivalence relations)   Recall that a partition $\Pi=\{B_1,\dots,B_k\}$ of a set $A$ defines an equivalence relation $\sim_{\Pi}$ on $A$ by the rule that for $a,b\in A$ we write $a\sim_{\Pi} b$ if $a$ and $b$ belong to the same block of the partition, i.e., if $(\exists i)(a,b\in B_i)$.

7.11 DO (uniqueness of partition)   Prove: Different partitions define different equivalence relations. In other words, let $\Pi$ and $\Psi$ be two partitions of the set $A$. Prove: if $\sim_{\Pi} = \sim_{\Psi}$ then $\Pi = \Psi$.

7.12 Fundamental Theorem of Equivalence Relations Let $\sim$ be an equivalence relation on the set $A$. Then $\sim$ arises from a unique partition. In other words, $(\exists!\text{ partition }\Pi\text{ of }A)(\sim = \sim_{\Pi})$.

7.13 COMMENT   The uniqueness part of the statement is the content of Exercise 7.11. The non-trivial part is the existence.

7.14 DEF   The blocks of $\Pi$ are called the equivalence classes of the relation $\sim$.
With these classes in mind, we can informally summarize the Theorem as saying that equivalence relations classify.
This result is fundamental to understanding how intelligent beings create concepts such as numbers, colors, etc. Natural numbers arise from the observation that certain pairs of sets have a bijection between them, and this relation among sets is an equivalence relation. Members of one of its equivalence classes are "three trees," "three mountain peaks," "three birds," etc., giving rise to the number "3"; each equivalence class corresponds to a natural number. Colors arise from the relation among objetcs of having the same color, although, as usual in practical concept forming, there are bordeline (hard to classify) cases.

7.15 DO   REVIEW the proof of the Fundamental Theorem given in class. Here is the idea. For $a\in A$ let $[a]=\{b\in A\mid a\sim b\}$. We refer to this as the "candidate equivalence class of $A$." We need to prove that the candidate equivalence classes partition $A$ and that $\sim$ corresponds to that partition. The proof goes through a series of observations.
7.15(a)   $a\in [a]$ (by reflexivity)
7.15(b)   If $a\in [b]$ then $[a]\subseteq [b]$ (by transitivity)
7.15(c)   If $a\in[b]$ then $b\in [a]$ (by symmetry)
7.15(d)   If $b\in[a]$ then $[a]=[b]$ (from (b) and (c))
7.15(e)   $[a]$ and $[b]$ are either disjoint or equal (from (d))
7.15(f)   $\bigcup_{a\in A} [a] = A$ (from (a)).

7.16 DEF   Given an equivalence relation $\sim$ on the set $A$, a system of representatives is a set $C\subseteq A$ such that $C$ contains exactly one element of each equivalence class. in particular, $|C|=$ the number of equivalence classes.

7.17 DEF (residue classes)  We have seen that for fixed $m$, the relation $a\equiv b \pmod m$ (congruence modulo $m$) is an equivalence relation among the integers. The equivalence classes of this relation are called the modulo $m$ residue classes.

7.18 DEF A system of representatives of the modulo $m$ residue classes is called a complete set of residues modulo $m$.

7.19 DO   The mod 5 residue classes are $5\zzz$, $5\zzz+1$, $5\zzz+2$, $5\zzz+3$, $5\zzz+4$.

7.20 DO   Let $m\ge 1$ and let $r_0,\dots,r_{m-1}$ be a complete set of residues mod $m$. Then the residue classes are $m\zzz+r_0$, $m\zzz+r_1$, $\dots$, $m\zzz+r_{m-1}$.

7.21 DO   What are the residue classes modulo $0$? (There are infinitely many of them!)

7.22 DO   Prove: if $m\neq 0$ then the number of mod $m$ residue classes is $|m|$.

Class 6, Thu, 10-17   Prime property, Fundamental Theorem of Arithmetic, congruences

Homework due Tuesday, October 22. Remember that problems 5.11, 5.17, 5.18, 5.36, 5.37B, 5.38B are also due on the 22nd.

6.1 DEF   A prime number is a positive integer with exactly two positive divisors.

6.2 DO   Observe that the number $1$ is not a prime number because it has just $1$ positive divisor.

6.3 DEF   A prime factorization of an integer $n$ is an expression of $n$ as a product of primes: $n=p_1\cdots p_k$.

6.4 EXAMPLE   Here is a prime factorization of the number $120$.    $120=2\cdot 2\cdot 2\cdot 3\cdot 5$. So $120$ is a product of $5$ prime factors. Another way of writing $120$ as a product of prime factors is $120=5\cdot 2\cdot 2\cdot 3\cdot 2$. The second expression differs from the first only in the order in which the prime factors are listed. This is necessarily so; this uniqueness up to ordering is the main content of the Fundamental Theorem of Arithmetic.

6.5 FUNDAMENTAL THEOREM OF ARITHMETIC. (a) Every positive integer can be written as a product of primes.   (b) This factorization is unique, up to the order of the prime factors.
Note: Part (a) is easy. The essence of the theorem is part (b) (uniqueness).

6.6 DO   Prove part (a) of the theorem by induction on $n$, the number to be factored. --- Note that the theorem holds for $n=1$: the number $1$ is the empty product of primes. This is your base case. Your job is the inductive step.

We now restate the uniqueness in greater detail.

6.7 THEOREM (Uniqueness of prime factorization) Lett $p_1,\dots,p_k, q_1,\dots,q_{\ell}$ be primes such that $p_1\cdots p_k =q_1\cdots q_{\ell}$. Then $k=\ell$ and there exists a bijection $f:[k]\to [k]$ such that $p_i = q_{f(i)}$.

6.8 DEF   We say that the integer $z$ has the prime property if $|b|\neq 1$ and $(\forall a,b\in\zzz)(z\mid ab \implies (z\mid a \text{ OR } z\mid b))\,.$

6.9 DO   If $n\in\zzz$ has the prime property then $-n$ also has the prime property.

6.10 DEF   An integer $n$ is a composite number $n >1$ and $n$ is not a prime number. In other words, $n$ is composite if $n$ can be written as $n=ab$ where $a,b >1$. (What quantifier is hidden in the "can be written" statement? Write this definition as a properly quantified formula.)

6.11 DO   Prove: If $n$ is a composite number then $n$ does not have the prime property.

6.12 DO   Prove: $0$ has the prime property.

6.13 PRIME PROPERTY THEOREM   If $p$ is a prime number then $p$ has the prime property.

This theorem is at the heart of the proof of the Fundam. Thm. of Arithmetic. It connects two opposite views of prime numbers: the definition of prime numbers speaks of the divisors of the given number; the prime property speaks about its multiples. The connection between the two is not evident and will require what we learned about the greatest common divisor, namely, Bézout's Lemma.

6.14 DO   If the number $p$ has the prime property and $p\mid a_1\cdots a_k$ then $(\exists i)(p\mid a_i)$.   Prove this by induction on $k$.

6.15 DO   Prove part (b) of the Fund. Thm. of Arithm. based on the Prime Property Theorem. Use induction on $n$.

The proof of the Prime Property Theorem is based on the following lemma.

6.16 HW (4 points)   If $a\mid bc$ and $d=\gcd(a,b)$ then $a\mid dc$.   (Hint: Use Béout's Lemma. Your proof should be very short, perhaps two lines, in any case not more than four lines.)

6.17 HW (3 points)   Use the preceding exercise to prove the Prime Property Theorem.   (Not more than 3 lines.)

6.18 DEF (Congruence)   Let $a,b,m\in \zzz$. We say that $a$ is congruent to $b$ modulo $m$, notation: $a\equiv b\pmod m$, if $m\mid a-b$.

6.19 Examples   $29\equiv 8 \pmod 7$,   $24 \equiv -2 \pmod{13}$,   $999\equiv 0 \pmod{37}$. (Verify.)

6.20 HW (2 points) Prove:   $a^2 \equiv b^2 \pmod{a+b}\,.$

6.21 DO   $a\equiv b\pmod 2$ if and only if $a$ and $b$ have the same parity, i.e., either both $a$ and $b$ are even or both $a$ and $b$ are odd.

6.22 DO   $a\equiv 0 \pmod m \iff m\mid a$

6.23 DO   $(\forall a,b)(a\equiv b\pmod 1)$

6.24 DO   $a\equiv b\pmod 0$ if and only if $a=b$.

6.25 DO   Prove: day $k$ and day $\ell$ of the month fall on the same day of the week if and only if $k\equiv\ell \pmod 7$. (This partly explains the term "calendar arithmetic.")

6.26 HW (1+1+4 points Fix $m$. So the relation $a\equiv b\pmod m$ is a relation on $\zzz$. Prove: this relation is an equivalence relation. State what property of divisibility you use in verifying each item in the definition of equivalence relations.

6.27 HW (4 points) Prove: If $a\equiv x \pmod m$ and $b\equiv y \pmod m$ then $a+b\equiv x+y \pmod m$. State what property of divisibility you use.

6.28 HW (3 points) Prove: If $a\equiv b \pmod m$ then $ac\equiv bc \pmod m$. State what property of divisibility you use.

6.29 HW (4 points) Prove: If $a\equiv x \pmod m$ and $b\equiv y \pmod m$ then $ab\equiv xy \pmod m$. Do not use properties of divisibility; use instead the exercises above about congruences. State what you use at each step of the proof.

6.30 HW (2 points) Prove:   $x^2 \equiv x \pmod 2$.

6.31 HW (3 points) Prove:   $x^3 \equiv x \pmod 3$.

6.32 Bonus (5 points) Prove:   $x^5 \equiv x \pmod 5$.

NOTE. The preceding three exercises are special cases of Fermat's little Theorem (FlT). Do not use FlT, even if you know how to prove it. Instead, give simple direct proofs.

6.33 FERMAT'S LITTLE THEOREM   If $p$ is a prime number then $x^p\equiv x\pmod p\,.$   (To be proved later)

6.34 HW (3 points) Prove: if $x$ is odd then $x^2 \equiv 1 \pmod 8$.

6.35 HW (3 points) True or false: $(\forall x)(x^4\equiv x \pmod 4)$. Give a clear answer and prove it.

6.36 DO   If $x\equiv \pm1 \pmod m$ then $x^2\equiv 1 \pmod m$.

6.37 HW (3 points)   Disprove the converse of the preceding exercise. In other words, prove that the following statement is false:   $(\forall m,x)(x^2\equiv 1 \pmod{m} \implies x\equiv \pm 1\pmod m$)

6.38 HW (3 points) Let $p$ be a prime number. Prove: if $x^2\equiv 1\pmod p$ then $x\equiv \pm1 \pmod p$. State the result you use.

6.39 HW (4 points, due Thursday) Prove: If $a\equiv b\pmod m$ then $\gcd(a,m)=\gcd(b,m)$.

6.40 HW (3 points) Find the smallest positive integer $n$ such that $n\equiv 3\pmod 7$ and $n \equiv 4 \pmod{11}$. Describe how you found your answer. No proof required.

6.41 DEF   Let $p$ be an odd prime number (i.e., $p\neq 2$). Let $1\le n\le p-1$. We say that $n$ is a quadratic residue mod $p$ if $(\exists x)(x^2 \equiv n\pmod p$. The numbers $1\le n\le p-1$ that are not quadratic residues are called quadratic nonresidues mod $p$.

6.42 DO   Verify: the mod 7 quadratic residues are $1, 2, 4\,$; the quadratic nonresidues are all that remain: $3,5,6\,$.

6.43 Bonus (5 points, due Thursday) Let $p$ be an odd prime number. Prove that there exists a quadratic nonresidue mod $p$. Do not use any result we have not proved in class or in homework assignments.

6.44 HW (5+2 points, due Thursday) (a) Prove:   $\gcd(3x+8, 5x+1)$ is either 1 or 37. (Proof: one line.)   (b) Find the smallest positive value of $x$ such that the gcd is 37. Describe how you found it. No proof required.

Class 5, Tue, 10-15   Counting, decision trees, relations, equivalence relations, partitions

Homework due Thursday, October 17.

WARNING: HW problem 5.12a was added on 10-16 at 1:30pm. (The problem was stated in class.)

5.1 DO   Review why we use the conventions that the empty sum is zero and the empty product is 1. Examples of the latter: $0!=1$, $0^0=1$.

5.2 Notation   $[n] = \{1,2,\dots,n\}$

5.3 DO   The number of functions $f : [n]\to[k]$ is $k^n$.  Proof. We make $n$ independent $k$-ary decisions.

5.4 DO   The number of injections $f : [n]\to[k]$ is $k(k-1)\dots(k-n+1)$.   Remark. Note that this number is zero when $k < n$, as it should be by the Pigeon Hole Principle.

5.5 DO   An $[n]\to [n]$ injection is a bijection.

5.6 DO   The number of $[n]\to [n]$ bijections is $n!=n(n-1)\cdots 2\cdot 1$ ($n$-factorial). For instance, $5! = 5\cdot 4\cdot 3\cdot 2\cdot 1=120.$

5.7 HW (4 points) Four medals are distributed among $n$ athletes: 1 gold, 1 silver, 2 bronze. (No athlete gets more than one medal.) Determine the number of possible outcomes. No proof required. Your answer should be a very simple, closed-form expression.   "Closed form" means you can use basic functions (addition, multiplication, taking powers, factorials), but no summation symbols or dot-dot-dots are permitted.

5.8 DO   Review decision trees. Root, parent node, children. The root is the only node without a parent; all other nodes have exactly one parent. A leaf is a node with no children. The depth of the tree is the longest path from the root to a leaf. The root is at level 0, the children of the root are at level 1, the children of a level-$i$ node are no level $i+1$.

5.9 DO   Suppose the root has $k_1$ children; each child of the root has $k_2$ children, each node on level $i-1$ has $k_i$ children; the leaves are on level $d$ (the depth of the tree). The the number of leaves is $$\prod_{i=1}^d k_i\ .$$

5.10 HW (3+1+6 points) Count (a) the $[n]\to [2]$ surjections,   (b) the $[n]\to [n]$ surjections,   (c) the $[n]\to [n-1]$ surjections.
Each answer should be a simple closed-form expression. No proof required, but formulas that are too complicated will earn no credit.

5.11 Bonus (5 points, due Tuesday) Count the $[n]\to [3]$ surjections.   (Added 10-18 3:38pm) No proof required. Give simple formula.

5.12 DEF   A relation on a set $A$ is a predicate on the set $A\times A$, i.e., a function $R : A\to \{0,1\}$. For $R(a,b)=1$ we usually write $aRb$ and say that the pair $(a,b)$ is in the $R$ relation.

5.12a HW (4 points) Let $|A|=n$. How many relations are there on $A$? Your answer should be a simple formula. No proof required.

5.13 DEF   $R$ is reflexive if $(\forall a\in A)(aRa)$

5.14 DEF   $R$ is symmetric if $(\forall a,b\in A)(aRb\implies bRa)$

5.15 DEF   $R$ is transitive if $(\forall a,b,c\in A)((aRb \text{ and } bRc)\implies aRc)$

5.16 Examples of transitive relations: $<$ and $\le$ relations among real numbers, divisibility among integers, the "ancestor" relation among humans, the "sibling or equal" relation among humans.

5.17 HW (3 points)   Prove: The "sibling" relation among humans is not transitive.

5.18 HW (4 points, due Tuesday)   Count the reflexive relations on $[n]$. Your answer should be a simple closed-form expression. No proof required, but formulas that are too complicated will earn no credit.

5.19 DEF   A relation $R$ on the set $A$ is irreflexive if $(\forall a\in A)(\neg\, aRa)$ where $\neg$ is the negation symbol, so $\neg\, aRa$ means $aRa$ does not hold.

5.20 HW (3 points) Find a relation that is neither reflexive nor irreflexive. Make your set $A$ (on which the relation is defined) as small as possible. No proof required.

5.21 DEF   An equivalence relation is a relation that is reflexive, symmetric, and transitive.

5.22 Examples: "sibling or equal", similarity of triangles in the plane, voting in the same state.

5.23 DEF   Let $f:A\to B$ be a function. Define the relation $R_f$ on $A$ as follows. For $a,b\in A$ we say $aR_f b$ if $f(a)=f(b)$. The relation $R_f$ is called the kernel of the function $f$.

5.24 DO   Prove: the kernel of a function is an equivalence relation on the domain of the function.

5.25 DO   Prove: every equivalence relation is the kernel of some function. In other words, let $R$ be an equivalence relation on the set $A$. Prove that there exists a set $B$ and a function $f :A\to B$ such that $R = R_f$.

5.26 DEF   A partition of a set $A$ is a representation of $A$ as the union of non-empty disjoint sets. We write $\Pi=\{B_1,\dots,B_k\}$ for the partition $A=B_1\dot\cup\dots\dot\cup B_m$ where the dots indicate that these sets are pairwise disjoint. The $B_i$ are called the blocks of $\Pi$.

5.27 Example.   The set $[3]$ has 5 partitions: $\Pi_1=\{\{1,2,3\}\}$,   $\Pi_2=\{\{1,2\},\{3\}\}$,   $\Pi_3=\{\{1,3\},\{2\}\}$,   $\Pi_4=\{\{2,3\},\{1\}\}$,   $\Pi_5=\{\{1\},\{2\},\{3\}\}$.

5.28 DEF   A function $f:A\to B$ defines the partition $$\Pi_f = \{f^{-1}(b)\mid b\in \range(f)\}$$ of the domain of $f$.

5.29 DO   Verify that $\Pi_f$ is indeed a partition, i.e., $$A=\dot\bigcup_{b\in\range(f)} \ f^{-1}(b)\,.$$

5.30 DO   Prove: Given a partition $\Pi$ of the set $A$, there exists a set $B$ and a function $f:A\to B$ such that $\Pi = \Pi_f$.

5.31 DEF   Given a partition $\Pi=\{B_1,\dots,B_k\}$ of the set $A$, define the relation $R_{\Pi}$ as follows: for $a,b\in A$ we say that $a R_{\Pi} b$ if $(\exists i)(a,b\in B_i)$, i.e., $a$ and $b$ belong to the same block of the partition.

5.32 HW (4 points)   Prove: $R_{\Pi}$ is an equivalence relation.

5.33 DO   Prove: given a partition $\Pi$ of the set $A$, there exists a set $B$ and a function $f:A\to B$ such that $R_{\Pi}$ is the kernel of $f$, i.e., $R_{\Pi}=R_f$.

5.34 DEF   The $n$-th Bell number $B(n)$ is defined as the number of partitions of $[n]$.

5.35 DO   Verify: $B(0)=1$, $B(1)=1$, $B(2)=2$, $B(3)=5$.

5.36 HW (due Tuesday, 5 points) Prove:   $B(n)\le n^n\,.$ Give a very simple surjective solution: find a surjection that maps the set of $[n]\to [n]$ functions onto the set of partitions of $[n]$. Give a clear definition of your surjection. Do not prove that it is indeed a surjection.

5.37 Bonus (due Tuesday, 5 points) Prove:   $B(n)\le n!$
Find an injective solution: give an injection from the set of partitions of $[n]$ to the set of permutations of $[n]$. Give a clear definition of your injection. Do not prove that it is indeed an injection.
A solution to this problem does not earn you credit for 5.36; you need to separately execute the instruction in 5.36 to earn credit for that problem.

5.38 Bonus (due Tuesday, 6 points) Prove:   If $0\le k\le n$ then $B(n) \ge k^{n-k}$. Give an injective solution: assign a partition to each function $f:[n-k]\to [k]$ such that distinct functions don't collide (they are not assigned the same partition). Give a clear definition of your injection. Do not prove that it is indeed an injection.

Class 4, Thu, 10-10   Euclid's algorithm, Bézout's Lemma

Homework due Tuesday, October 15. Remember that problems 3.1 (Bonus) and 3.3 (HW) are also due on the 15th.

4.1 DO   Study the Euclid's algorithm handout.

4.2 DO   29 is a 2-digit number in base 10 and a 5-digit number in binary (base 2). How many digits does it have in base 3?

4.3 DO   Let $b$ be a positive integer with $n$ digits in base $t$. (a) Prove:   $t^{n-1} \le b \le t^n-1$.
(b) HW (3 points)   Prove:   $\displaystyle{n = \left\lceil \frac{\log (b+1)}{\log t} \right\rceil}$.
WARNING. There was a typo in the previously posted version of this problem: it erroneously had $\log b$ instead of $\log (b+1)$ in the numerator. Thank you to a student in class for pointing out the error. Fixed 10-13 9:20pm.
($\lceil x\rceil$ denotes the rounded-up value of $x$ and is called the "ceiling" of $x$. For instance, $\lceil 3.2\rceil=4$, $\lceil -3.2\rceil=-3$, $\lceil 3\rceil=3$.)

4.4 Discussion: Is Euclid's algorithm efficient?   We use the notation from the handout. $a$ and $b$ are non-negative integers and the task is to determine $\gcd(a,b)$. The values $a,b$ are fixed throughout the algorithm; the algorithm manipulates variables $A$ and $B$ (also non-negative integers).
Euclid's algorithm proceeds in rounds; each round is an execution of the while loop. The algorithm exits the while loop and terminates when $B=0$. The question is, how many times does the algorithm need to execute the while loop. We noted that the algorithm is guaranteed to terminate because the value $B$ is reduced in each round. But this only guarantees that the algorithm will take no more than $b$ rounds. If $b$ is an $n$-bit integer (has $n$ digits in binary) then $b\approx 2^n$ (more precisely, $2^{n-1}\le b < 2^n$), so taking $b$ rounds would be prohibitive even for numbers with 100 binary digits: the number of rounds would grow exponentially as a function of the bit-length of the input. Actually, Euclid's algorithm is very efficient, as the next exercise shows.

4.5 HW (6 points) Let $a, b$ be $n$-bit positive integers. Prove that Euclid's algorithm to determine $\gcd(a,b)$ terminates in at most $2n$ rounds.   Hint. Prove the following lemma: The number of bits of $B$ goes down by at least one in every other round. To show this, prove the following. If $B_k$ denotes the value of $B$ in round $k$ then $B_{k+2}\le B_k/2$.   Your solution should take just a few lines.

4.6 DEF: Fibonacci numbers.   The sequence of Fibonacci numbers is defined by the initial values $F_0=0$ and $F_1=1$ and the recurrence $F_n=F_{n-1}+F_{n-2}$ for $n\ge 2$. So the sequence begins with $0,1,1,2,3,5,8,13,21,34,55,89,\dots$.

4.7 DO   Review mathematical induction from your class notes. We discussed it in detail, both the principle and several examples. Use induction in the next exercises. Clearly state the Inductive Hypothesis, the inductive step, and the base cases.

4.8 HW (5 points)   Prove that consecutive Fibonacci numbers are relatively prime. In other words,   $(\forall n\ge 0)(\gcd(F_n, F_{n+1})=1)$.

4.9 Bonus (6 points)   Prove: $(\forall k,\ell\ge 0)(\gcd(2^k-1,2^{\ell}-1)=2^d-1$ where $d=\gcd(k,\ell))$.

4.10 CH   Prove: $(\forall k,\ell\ge 0)(\gcd(F_k, F_{\ell})=F_d$ where $d=\gcd(k,\ell))$.   The next exercise may be helpful.

4.11 Bonus (4 points)   Let $A$ denote the $2\times 2$ matrix $$A=\left(\matrix{0 & 1 \\ 1 & 1}\right) .$$ Determine $A^n$. Prove your answer.

4.12 DEF   Let $a,b\in\zzz$. We say that the integer $c$ is a linear combination of $a$ and $b$ with integer coefficients if $(\exists x,y\in\zzz)(c=ax+by)$. When speaking of integers, we shall omit the words "integer coefficients" and simply speak of linear combinations, with the tacit assumption that the coefficients are integers.

4.13 DO   Observe that the set of linear combinations of the integers $a$ and $b$ is the set $a\zzz + b\zzz$. "Observe" means you should argue that this is immediate from the definitions involved.

4.14 HW (4 points) Let $a,b\in\zzz$. Prove: if $d$ is a common divisor of $a$ and $b$ and $d$ can be written as a linear combination of $a$ and $b$ then $d$ is a greatest common divisor of $a$ and $b$. In other words, if $d\in \Div(a,b)\cap (a\zzz+b\zzz)$ then $d = \pm \gcd(a,b)$.

4.15 THEOREM ("Bézout's Lemma").   The $\gcd$ of two numbers can always be written as a linear combination of the two numbers. In other words, $(\forall a,b\in \zzz)(\exists x,y\in \zzz)(\gcd(a,b)=ax+by)$.

4.16 DO   Review the proof of Bézout's Lemma using Euclid's algorithm.

4.17 HW (5 points)  Solve the equation $7=56x+77y$ in integers $x,y$ using Euclid's algorithm. First write down each step of Euclid's algorithm that leads to the fact that $\gcd(77,56)=7$ and then follow the steps of Euclid's algorithm in reverse to represent $7$ as a linear combination of each pair $(A,B)$ of integers definded in each round of Euclid's algorithm. Follow the description of the algorithm in the handout.

4.18 STUDY (Golden ratio)   The positive solution to the equation $x^2-x-1=0$ is called the Golden ratio; its value is $\phi = (1+\sqrt{5})/2 = 1.6180339887\dots$.

4.19 Reward problem. (Your reward is the beauty of the fact and the solution; do not hand it in.) Take a regular pentagon. Let $a$ denote the length of a side and $b$ the length of a diagonal. Prove: $b/a = \phi$.

4.20 Bonus (proportion of consecutive Fibonacci numbers) (5 points) The limit $\lim_{n\to\infty} F_{n+1}/F_n$ exists, but I am not asking you to prove this. Prove: if this limit exists, its only possible value is the golden ratio.   Your proof should take no more than five lines. Proofs longer than 10 lines will not be accepted.

4.21 HW (-30 points if ignored)   If you have not aswered the questionnaire yet, do it by Tuesday.

Class 3, Tue, 10-8   Functions, collisions, greatest common divisor

3.1 Bonus (due Tue, 10-15) (5 points) The $8\times 8$ chessboard has 64 cells. It can be tiled by 32 dominoes (in many ways). A domino is either in a horizontal or in a vertical position and always covers two neighboring cells. Now remove two opposite corner cells from the chessboard. Prove that it is impossible to tile the remaining 62 cells by dominoes. Your proof must be an "AH-HA" proof (immediately convincing argument). If you write more than four lines, you are on the wrong track, do not hand it in. Do not look up the solution on the web.

3.2 HW Let $A, B$ be sets, $|A|=n$, $|B|=n-10$. Consider all functions $f : A\to B$.
(a) (6 points) What is the minimum possible number of collisions of $f$ (minimum over all choices of $f$) assuming $n\ge 20$ ?
(b) (Bonus) (5 points) Same, assuming $n\ge 11$ only.

3.2(c) In class.   Let $f : A\to B$ where $|A|=n$ and $|B|\ge 1$. What is the maximum possible number of collisions? Answer: the constant functions have the maximum number of collisions, namely, if $f$ is a constant function ($f(x)$ is the same value for all $x\in A$) then every pair of elements of $A$ collides. There cannot be more collisions than that. The number of pairs from $A$ is $n(n-1)/2$ (why?), so this is the maximum number of collisions.

3.3 HW (due Tue, 10-15) (6 points) Let $A\subset \zzz$ be a finite set of integers, $|A|=n$. Determine the maximum size of $|A+A|$ (maximum over all choices of the $n$-element set $A$). Your answer should be a simple function of $n$. To prove your answer, you need to give a matching lower and upper bound on this maximum.

3.4 DEF   The integer $d$ is a greatest common divisor (gr.c.d.) of the integers $a$ and $b$ if the following two statements hold.
(a)   $d$ is a common divisor, i.e., $d\mid a$ and $d\mid b$ (b)   $d$ is a common multiple of all common divisors, i.e., $(\forall e)((e\mid a \text{ and } e\mid b)\implies e\mid d)$.

3.5 NOTATION   We write $\Div(a)$ to denote the set of divisors of the integer $a$. For instance, $\Div(6)=\{\pm 1, \pm 2, \pm 3, \pm 6\}$. Notation: $\Div(a,b)=\Div(a)\cap\Div(b)$. This is the set of common divisors of $a$ and $b$.

3.6 DO   Verify: (a) $\Div(a)=\Div(-a)$   (b) $\Div(0)=\zzz$   (c) $\Div(a,a)=\Div(a)$   (d) $\Div(a,0)=\Div(a)$   (e) $\Div(a,b)=\Div(b,a)$   (f) $\Div(a,b)=\Div(a,-b)$

3.7 DO   Prove: $d$ is a gr.c.d. of $a$ and $b$ if and only if $\Div(a,b) = \Div(d)$

3.8 HW (Euclid's Lemma, modern version) (5 points) Prove:   $\Div(a,b)=\Div(a-b,b)$.

3.9 THEOREM (existence of gr.c.d.) Every pair of integers has a greatest common divisor.
Proof. Given $a,b\in\zzz$ we need to find $d\in\zzz$ such that $\Div(a,b)=\Div(d)$.
By 3.6(f) we may assume $a, b\ge 0$. We proceed by induction on $a+b$. We shall have infinitely many base cases, namely, those when $a=0$ or $b=0$. If $b=0$ then $d=a$ works by 3.6 (d). If $a=0$ we use (e) to swap $a$ and $b$ so now $b=0$ and we are done.
Assume now that $a,b >0$. The Inductive Hypothesis is that for any $a',b'\ge 0$ such that $a'+b' < a+b$ there exists $d$ such that $\Div(a',b')=\Div(d)$.
Again swapping $a$ and $b$ if necessary we may assume $a\ge b$. Now, by 3.8 (Euclid's lemma), we have $\Div(a,b)=\Div(a-b,b)$. Applying the Inductive Hypothesis to $a'=a-b$, $b'=b$ we see that there exists $d$ such that $\Div(a',b')=\Div(d)$. The reason we were able to use the Inductive Hypothesis is that $a'+b' = a < a+b$. So we conclude that $\Div(a,b)=\Div(a-b,b)=\Div(d)$. This completes the proof.

3.10 DO (ambiguity of gr.c.d)   (a) Prove that if $d$ is a gr.c.d. of $a$ and $b$ then $-d$ is also a gr.c.d.   (b) Prove: there are no other gr.c.divisors of $a$ and $b$.

3.11 CONVENTION   If $d$ is a gr.c.d. of $a$ and $b$ then we write $\gcd(a,b)=|d|$ (we select the nonnegative gr.c.d.)

3.12 DO   Prove: under this convention, $\gcd(a,a) = |a|$.

3.13 DO (Euclid's ancient lemma)   Prove:  $\gcd(a,b)=\gcd(a-b,b)$.

3.14 DO   Review induction.

Class 2, Thu 10-3   Sets, functions, divisibility

Unless otherwise stated, the universe of the quantifiers is $\zzz$, the set of integers. Posted 10-6 at 6:30pm. Problems 2.35 and 2.36 added 10-7 at 2am.

2.1 HW (3 points)   Find all sets $A\subseteq\zzz$ such that the following holds: $(\forall x)(x\in A \implies x=3)$

2.2 DO   Prove:  $(\forall a,b)((a\mid b \text{ and } b\mid a) \implies a = \pm b)$

2.3 DO   Which integers are divisible by all integers? In other words, find all values of $b$ such that   $(\forall a)(a\mid b)$.

2.4 In class:   $a\mid b \text{ and } a\mid c \implies a\mid b+c$.
As an example of the architecture of mathematics, we found that this property of divisibility follows from a basic property of arithmetic ("ground floor"): the distributivity of multiplication over addition.
Convention. In this statement we omitted the universal quantifier $(\forall a,b,c)$. This is the general convention: all free variables count as universally quantified. For instance, when we say "$a+b=b+a$ hold for integers," we mean that $(\forall a,b)(a+b=b+a)$.

2.5 DO   Prove:   $a\mid b \text{ and } a\mid c \implies a\mid b-c$.

2.6 HW (8 points)   Find all integers $x$ such that $x+5\mid x$. Prove that your list is correct (the values you list satisfy the condition) and complete (you found all values that satisfy the condition).

2.7 DEF (Cartesian product of sets)   $A\times B = \{(a,b)\mid a\in A, b\in B\}$

2.8 Facts:   Let $A, B$ be finite sets. $A\dot\cup B$ means the "disjoint union of $A$ and $B$," i.e., it is the union of $A$ and $B$ under the assumption that $A\cap B=\emptyset$.
With this notation we have $|A\dot\cup B|=|A|+|B|$ and $|A\times B|=|A|\cdot|B|$.
These are not theorems but essentially the definitions of addition and multiplication of numbers, inferred from operations with finite sets.

2.9 DEF   Let $A, B$ be sets. A function $f : A\to B$ with domain $A$ and codomain is an assignment of a unique value $f(a)\in B$ to each $a\in A$. (Formally we are talking about a subset $F\subseteq A\times B$ such that $(forall a\in A)(\exists! b)((a,b)\in F)$ and we write $f(a)$ to denote this unique $b$ associated with $a$. ($(\exists! b)$ reads "there exists a unique $b$.")

2.10 DEF   The range of $f$ is the set $\range(f) = \{f(a) \mid a\in A\}$.

2.11 HW (3 points)   Give an equivalent definition of the range in the form $\range(f) = \{b\in B \mid \text{ some property of } b\}$. You have to give a formal statement of the "property of $b$" that puts $b$ in the range of $f$. This statement will involve a quantifier.

2.12 DO   Note that the range is a subset of the codomain: $\range(f) \subseteq B$.

2.13 In class:   If $|A|=k$ and $|B|=\ell$ then the number of functions $f : A\to B$ is $\ell^k$.

2.14 Notation: $B^A$ denotes the set of functions $f:A\to B$.
With this notation, 2.13 asserts that $|B^A|=|B|^{|A|}$.

2.15 DEF   A function $f : A\to B$ is surjective if $\range(f)=B$. A surjective function is called a surjection.

2.16 DO   Prove:   $f : A\to B$ is surjective if and only if $(\forall b\in B)(\exists a\in A)(f(a)=b)$.

2.17 Fact.   If there exists a surjection from $A$ to $B$ then $|A| \ge |B|$.

2.18 In class:   Let $A,B$ be finite subsets of $\zzz$. Then $|A+B| \le |A|\cdot |B|$.
Proof:  Consider the function $f: A\times B \to A+B$ defined by $f(a,b)=a+b$. This is a surjection. QED

2.19 DEF   Let $f :A\to B$ be a function. We say that the pair $\{a_1, a_2\}\subseteq A$ collides if $a_1 \neq a_2$ but $f(a_1)=f(a_2)$.

2.20 DEF   The function $f : A\to B$ is injective if there are no collisions. An injective function is called an injection.

2.21 DO   The function $f : A\to B$ is injective if and only if $(\forall a_1,a_2\in A)(f(a_1)=f(a_2)\implies a_1=a_2)$.

2.22 Fact (Pigeon Hole Principle).   If there exists an injection from $A$ to $B$ then $|A|\le |B|$. In other words, if $|A|>|B|$ then every function $f :A\to B$ has a collision. (DO: Verify that these two statements are equivalent.)

2.23 DEF   The function $f : A\to B$ is bijective if it is both injective and surjective.

2.24 DEF   We say that the function $g :B\to A$ is the inverse of the function $f:A\to B$ if $(\forall a\in A)(g(f(a))=a)$ and $(\forall b\in B)(f(g(b))=b)$.

2.25 DO   Prove: a function is bijective if and only if it has an inverse.

2.26 DO   Prove: a function cannot have more than one inverse.

2.27 DO   If there exists a bijection from $A$ to $B$ then $|A|=|B|$.

2.28 DEF (Predicate)   A predicate over the set $A$ is a function $f : A \to \{0,1\}$.

2.29 DO   Prove: the number of predicates over the finite set $A$ is $2^{|A|}$.   (Hint: this is a special case of Ex. 2.13.)

2.30 DEF (Characteristic function)   Let $B\subset A$. We define the characteristic function of $B$ relative to $A$ as the predicate $f_B : A\to \{0,1\}$ defined by $$ f_B(x) = \begin{cases} 1 &\text{ if }& x\in B \\ 0 &\text{ if }& x \in A\setminus B \end{cases} $$

2.31 DEF   The powerset of a set $A$, denoted $\calP(A)$, is the set of subsets of $A$. In other words, $\calP(A) = \{B\mid B\subseteq A\}$.

2.32 In class. Counting subsets: a bijective proof.
Theorem.  If $|A|=n$ then $|\calP(A)|=2^n$.
Proof.   The correspondence $B\mapsto f_B$ is a bijection from the powerset $\calP(A)$ to the set $\{0,1\}^A$ of predicates over $A$. (DO: Verify this statement!) It follows that $|\calP(A)|=2^{|A|}=2^n$.

2.33 Bonus (6 points): even vs. odd subsets - a bijection.   We say that a finite set $B$ is even is $|B|$ is an even number, and the set $B$ is odd if $|B|$ is odd. Let $A$ be a set of $n$ elements, $n\ge 1$. Let $\even(A)$ denote the set of even subsets of $A$ and $\odd(A)$ the set of odd subsets of $A$. Find a bijection $f: \even(A)\to \odd(A)$. Your bijection must have a very simple definition. Define $f$. Prove that $f$ is a bijection by also defining its inverse, $g$. You do not need to show the details of how you verify that $g$ is indeed the inverse of $f$. -- Point our where in your proof you use the assumption that $n\ge 1$.

2.34 DO   Use the preceding exercise to show that the number of even subsets of a set of $n$ elements is $2^{n-1}$.

2.35 HW (4 points): left vs. right inverse.   Find sets $A,B$ and functions $f:A\to B$ and $g: B\to A$ such that the first equation in Def. 2.24 hold but the second does not, i.e., $(\forall a\in A)(g(f(a))=a)$ but not $(\forall b\in B)(f(g(b))=b)$. Make $|A|+|B|$ as small as possible. No proofs are needed, just state your sets $A, B$ and define your functions $f,g$.

2.36 Bonus (6 points): number of divisors.   Let $d(n)$ denote the number of positive divisors of the positive integer $n$. For instance, $d(4)=3$, $d(5)=2$, $d(6)=4$. (Check!)   Prove the inequality   $d(n) < 2\sqrt{n}$   for all $n\ge 1$.

Class 1, Tue 10-1   Quantifiers, sets, divisibility

1.1 Quantifiers $\forall$ "for all" (the universal quantifier)    and $\exists$ "there exists $\dots$ such that" (the existential quantifier). We need to specify a "universe of reference", which is a set $U$ and $\forall x$ means $\forall x\in U$ and $\exists x$ means $\exists x\in U$. The universe is usually clear from the context.

1.2 DEF Subset We say that the set $A$ is a subset of the set $B$ if $(\forall x)(x\in A \implies x\in B)$. We denote this circumstance by $A\subseteq B$.   For example, $\{a,b,a,a\}\subseteq \{a,c,b\}$.

1.3 When are two sets equal? Let $A,B$ be sets. Then $A=B \iff (\forall x)(x\in A \iff x\in B)$. In other words, $A$ and $B$ have the same elements.   For example, $\{a, c, a, b, c\} = \{a ,c ,b\} = \{a, b, c\}$. There is just one empty set $\emptyset$ defined by $(\forall x)(x\notin \emptyset\}$.

1.4 DO   Prove: $A=B$ if and only if $A\subseteq B$ and $B\subseteq A$.

1.5 DEF (sumset)   Let $A,B$ be subsets of $\zzz$, the set of integers. We define their sumset as   $A+B = \{a+b \mid a\in A, b\in B\}$.   This is an example of the "setmaker bar" notation; the bar reads "such that."

1.6 Example   Let $A=\{3,4,5,8\}$ and $B=\{1,6,7\}$. Then $A+B = \{4,5,6,9,10,11,12,14,15\}$.

1.7 DO   Prove:  $A+B=\{c\in\zzz\mid (\exists x\in A)(\exists y\in B)(c=x+y)\}$

1.8 DO   $A+\emptyset = \emptyset$.

1.9 NOTATION   For a set $A$ we write $|A|$ to denote the number of elements of $A$, also called the cardinality of $A$, or simply the size of $A$. For instance, $|\{a,c,a,b,c\}|=3.$

1.10 HW (6 points) Let $A,B$ be non-empty finite subsets of $\zzz$. Prove:   $|A+B|\ge |A|+|B|-1.$

1.11 DO   Prove that the upper bound given in the preceding exercise is tight. In other words, for all $k,\ell\ge 1$, find $A,B\subseteq\zzz$ such that $|A|=k$, $|B|=\ell$, and $|A+B|=k+\ell-1$.

1.12 DO   Let $A,B$ be finite subsets of $\zzz$. Prove:   $|A+B|\le |A|\cdot |B|$.

1.14 DEF   Let $A\subseteq \zzz$ and $k\in \zzz$. Then $kA = \{ka \mid a\in A\}$.

1.15 Examples (DO: verify!):   $1\zzz=\zzz$,   $2\zzz=\{\text{even numbers}\}$,   $0\zzz =\{0\}$.

1.16 DEF (divisibility) Let $a,b\in\zzz$. We say that $a$ is a divisor of $b$ is $(\exists x\in\zzz)(ax=b)$. Other expressions we use to describe the same concept: $a$ divides $b$,   $b$ is a multiple of $a$.

1.17 DO   $(\forall a\in\zzz)(a\mid a)$. NOTE: this is true even for $a=0$ (why?):   $0\mid 0$.

1.18 DO   $b\in kA \iff (\exists a\in A)(b=ka)\}$.

1.19 DO   $kA = \{b\in\zzz\mid a\text{ divides }b\}$.

1.20 HW (3 points) Find $k$ such that $4\zzz + 6\zzz = k\zzz$. No proof required.

1.21 DEF (intersection) $A\cap B= \{x\mid x\in A\text{ and }x\in B\}$.

1.22 HW (3 points) Find $\ell$ such that $4\zzz \cap 6\zzz = \ell\zzz$. No proof required.

1.23 DO (transitivity of divisibility) Prove: if $a\mid b$ and $b\mid c$ then $a\mid c$. Note that this follows from the associativity of multiplication: $(pq)r=p(qr)$ (lower level in the architecture of mathematics --- we build on that level).

1.24 CONVENTION   If we state a formula with free variables such as $(pq)r=p(qr)$, the intended meaning is that the formula holds for all choices of those free variables, as if they were universally quantified: $(\forall p,q,r)((pq)r=p(qr))$.

1.24 DO   Prove: if $a\mid b$ and $a\mid c$ then $a\mid b+c$ and $a\mid b-c$. What property of arithmetic do we use in the proof? (Distributivity: $p(q+r)=pq+pr$.)

1.25 DIVISOR GAME. Fix an integer $n\ge 2$. Two players alternate picking positive divisors of $n$. Multiples of a number picked cannot be picked in the future. The player forced to pick $n$ loses.
EXAMPLE: $n=30$. First move: Player 1 picks 10. This rules out picking 10, 5, 2, or 1 in the future.
Second move: Player 2 picks 3. (So in the future neither player can pick 10, 5, 3, 2, or 1.) Third move: Player 1 picks 6. Fourth move: Player 2 picks 15. Now all maximal divisors of 30 (6,10,15) have been picked, so Player 1 is left with no choice but to pick 30 in the Fifth move, and loses.

1.26 DO   Prove that if $n=30$ and Player 1 begins with any number other than 1 then Player 1 loses (assuming Player 2 plays right).

1.27 DO   Prove: for $n=30$, Player 1 has a winning strategy. What is the first move of Player 1 ?

1.28 DO   Prove: for $n=81$, Player 1 has an easy winning strategy. (More generally, Player 1 easily wins if $n$ is a prime power ($n=p^k$ for some prime $p$ and $k\ge 1$)). What is the first move of Player 1 ?

1.29 DO   Prove: for $n=36$, Player 1 has an easy winning strategy. (More generally, Player 1 easily wins if $n$ is of the form $n=p^2q^2$ where $p,q$ are distinct primes.) What is the first move of Player 1? What is their strategy?

1.30 CH   For every $n\ge 2$, Player 1 has a winning strategy.