Decision tree complexity

Definition 1.1   A boolean function in $n$ variables is a function $f:\{0,1\}^n\to\{0,1\}$. Boolean functions are also referred to as ``properties.''

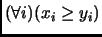
Definition 1.2   A property (boolean function) of several boolean variables is monotone increasing if its truth on an input implies its truth on any input in which at least the same variables are true (but some of the falses may have become true), i.e., if $f(x_1,\dots,x_n)\ge f(y_1,\dots,y_n)$ whenever $(\forall i)(x_i\ge y_i)$. A property is monotone if either it or its negation is monotone increasing.

``Graph properties'' are boolean functions of the $\binom{v}{2}$ boolean variables expressing adjacency ($v$ is the number of vertices); such a function must take the same value on isomorphic graphs, so the function must be invariant under the group $S_v^{(2)}$, the induced action of $S_v$ on the $\binom{n}{2}$ pairs. Connectedness is a monotone increasing property. Planarity is monotone decreasing.

Definition 1.3   A decision tree is an algorithm for computing a function of an unknown input. Each vertex of the tree is labeled by a variable and the branches from that node are labeled by the possible values of the variable. The leaves are labeled by the output of the function. The process starts at the root, knowing nothing, works down the tree, choosing to learn the values of some of the variables based on those already known and eventually reaches a decision. The decision tree complexity of a function is the minimum depth of a decision tree that computes that function. A property is evasive if its decision tree complexity is equal to the number of variables.

Conjecture 1.4   All nontrivial (i.e., nonconstant) monotone graph properties are evasive.

Theorem 1.5 (Rivest-Vuillemin)   A nontrivial monotone graph property has decision tree complexity at least $v^2/16$ (a constant fraction of the maximum).

Theorem 1.6 (Rivest-Vuillemin)   If $q$ is a prime power, and $f \colon \{0,1\}^q \to \{0,1\}$ is a boolean function that is invariant under the action of a transitive permutation group acting on the $q$ variables, and $f(\underline{0}) \ne f(\underline{1})$, then $f$ is evasive. (No assumption of monotonicity is needed.)

Conjecture 1.7   A monotone function invariant under a transitive group acting on the variables is evasive.

Conjecture  is a special case of this. The group in that case is primitive ($S_v^{(2)}$). The case of other primitive groups are also of interest.

Proof of the Rivest-Vuillemin Theorem was given in class for a prime number of variables.