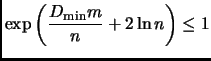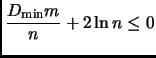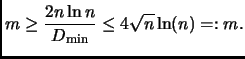Large primitive groups

For large $n$, the largest four primitive permutation groups are $S_n$ and $A_n$, of order about $n!$, and $S_k^{(2)}$ (for $n=\binom{k}{2}$) and $S_k\wr S_2$ (for $n=k^2$), of order about $e^{c\sqrt n\log n}$. The classification of finite simple groups allows us to show that these are the largest and even to list the largest down to size about $e^{\log^2 n}$. We can do reasonably well with elementary means.

Theorem 2.1   Assume $G<S_n$, $A_n \nless G$, and $G$ is primitive.

1. (Bochert c.1890) $\vert G\vert\le \frac{n!}{(n+1)/2)!}\approx e^{\frac n2\log n}$.
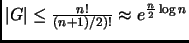2. (Wielandt, Praeger-Saxl, 1980) $\vert G\vert<4^n$.
3. (Babai, 1981) If 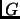$G$ is not doubly transitive, $\vert G\vert<e^{4\sqrt n\log^2n}$ (using almost only graph theory).

The following theorem si proved using the classification of finite simple groups; one can get close by elementary means.

Theorem 2.2   If $G\le S_n$, $G\not\ge A_n$ is doubly transitive then $\vert G\vert<n^{1+\log_2 n}.$

Remarks about symmetry and regularity: symmerty conditions are given in terms of automorphisms; regularity conditions in terms of numerical parameters. Symmetry condition imply regularity conditions (e.g., vertex-transitivity is a symmetry condition, which implies that the graph is regular, a regularity condition). The converse is seldom true. We shall define regularity conditions on a family of edge-colored digraphs which capture some combinatorial consequences of primitive group action. Using this translation, we shall prove a combinatorial result which implies a nearly optimal upper bound on the order of uniprimitive (primitive but not doubly transitive) permutation groups.

Picture of $D_6$. $R_0 = \Delta = \{(x,x) \mid x \in \Omega\}$, diagonal. $\Omega \times \Omega = R_0 \cup R_1 \cup \dots \cup R_{r-1}$. $r =$# colors = # orbits of $G$ on $\Omega \times \Omega$. $D_6$ has rank $4$, $r = 4$. In this case, all orbitals are self-paired.

Definition 2.3   An orbital $\Gamma$ of a permutation group $G\le \Sym(\Omega)$ is an orbit of $G$ on the set of ordered pairs ( $\Gamma\subset\Omega\times\Omega$). $\Gamma$ is self-paired when $\Gamma=\Gamma^{-1}$ (i.e., for $(x,y)\in \Gamma$ there exists $\sigma\in G$ such that $x^{\sigma}=y$ and $y^{\sigma}=x$). The rank $r$ of a permutation group is the number of its orbitals.

Definition 2.4   COHERENT CONFIGURATION of rank $r$:
$\ensuremath{\mathfrak{X}}= (\Omega; R_0, \dots, R_{r-1})$, $R_i \subseteq \Omega \times \Omega$.
$\Omega \times \Omega = R_0 {\mathbin{\dot{\cup}}}\dots {\mathbin{\dot{\cup}}}R_{r-1}$.
$X_i = (\Omega, R_i)$, $i$'th color digraph, called a constituent digraph. The color of a pair $x,y$ is defined as $c(x,y) = i$ if $(x,y) \in R_i$.
To be coherent, the following 3 axioms must be satisfied:

A1:

The diagonal is $\Delta = R_0 {\mathbin{\dot{\cup}}}\dots {\mathbin{\dot{\cup}}}R_{i_0 - 1}$. Equivalently, $c(x,x) = c(y,z) \Rightarrow y=z$.

A2:

$(\forall i)(\exists j)(R_j = R_{i}^{-1})$. Terminology: $R_i$ is self-paired if $R_i = R_{i}^{-1}$, i.e., $X_i$ is undirected.

A3:

$(\exists p_{i,j,k})(\forall (x,y) \in R_i) (\char93 \{z \mid c(x,z) = j, c(z,y) = k\} = p_{i,j,k})$

Definition 2.5   For $G \le \Sym(\Omega)$, $\ensuremath{\mathfrak{X}}(G) := (\Omega;$   orbitals$)$. We refer to these as ``the group case.''

Remark 2.6   There exist coherent configurations without a group. In fact, there are exponentially many rank-3 coherent configurations with no automorphisms.

Well, we always lose in translation. The question is how much.

Definition 2.7   $\ensuremath{\mathfrak{X}}$ is homogeneous if $R_0 = \Delta$ (i.e., $(\forall x,y)(c(x,x) = c(y,y))$).

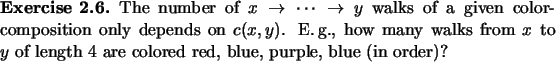
By the way, $\sum_{i=0}^{r-1} \rho_i = n$, since every vertex is connected to every other (including itself) in the graph $\cup X_i$, whose edge set contains all $n^2$ ordered pairs.

Definition 2.8   $\ensuremath{\mathfrak{X}}$ is a primitive coherent configuration if $\ensuremath{\mathfrak{X}}$ is homogeneous and ALL constituent digraphs $X_i$, $i \ge 1$ are connected.

Definition 2.9   $\ensuremath{\mathfrak{X}}$ is uniprimitive coherent configuration if $\ensuremath{\mathfrak{X}}$ is primitive and rank $\ge 3$.

$G \le \Sym(\Omega)$, $\Psi \subseteq \Omega$. Look at the pointwise stabilizer, $G_{\Psi}$, $= \cap_{x \in \Psi} G_x$. If $G_{\Psi} = \{1\}$, then $\vert G\vert \le n^{\vert\Psi\vert}$, in fact $\vert G\vert \le n(n-1) \dots (n-\vert\Psi\vert+1)$. Call such a $\Psi$ a ``fixing set.''

We shall prove, using only elementary graph theoretic arguments, that

Theorem 2.10   If $G$ is uniprimitive, then $\vert G\vert < e^{4 \sqrt{n} (\ln n)^2}$.

Lemma 2.11   If $G$ is uniprimitive, then $(\exists \Psi \subseteq \Omega) (\vert\Psi\vert \le 4 \sqrt{n} \ln n$    and $G_\Psi = \{1\})$.

Examples: How large is the smallest fixing set for various classes of permutation groups?

Definition 2.12   $z$ distinguishes $x$ and $y$ if $c(x,z) \ne c(y,z)$. $D(x,y) = \{z \mid c(x,z) \ne c(y,z) \}$ is the distinguishing set for $x,y$.

Definition 2.13   A distinguishing set of $\ensuremath{\mathfrak{X}}$ is any set $\Psi \subseteq \Omega$ such that $(\forall x \ne y)(\Psi \cap D(x,y) \ne \emptyset)$. In other words, for every pair $x,y$, $\Psi$ contains an element which distinguishes them.

Theorem  will follow from the following result.

Theorem 2.14   If $\ensuremath{\mathfrak{X}}$ is a uniprimitive coherent configuration, then there exists a distinguishing set $\Psi$ such that $\vert\Psi\vert < 4 \sqrt{n} \ln n$.

This will be an immediate consequence of the following. From now on, let us always assume $\ensuremath{\mathfrak{X}}$ is a uniprimitive coherent configuration.

Theorem 2.15 (Main technical theorem)   For every $x,y$, $\vert D(x,y)\vert \ge \sqrt{n}/2$.

Proof. [Main technical theorem $\Rightarrow$ Theorem ]. Pick $u_1, \dots, u_m$ at random, and hope that we picked enough to hit each $D(x,y)$.

$$\Prob(D(x,y) ) = \left(1 - \frac{\vert D(x,y)\vert}{n} \right)^m$$

$$\le \exp\left (-\frac{\vert D(x,y)\vert m}{n} \right).$$

Hence, by the Union Bound,

$$\Prob((\exists x,y)(D(x,y) )) < \binom{n}{2} \exp\left(-\frac{{D_{\mathrm{min}}}m}{n} \right)$$

$$< \exp\left(-\frac{{D_{\mathrm{min}}}m}{n} + 2 \ln n\right),$$

where ${D_{\mathrm{min}}}= \min_{x \ne y} \vert D(x,y)\vert$.

For this, it is sufficient to show

$$\exp\left(\frac{{D_{\mathrm{min}}}m}{n} + 2 \ln n\right) \le 1$$

or equivalently

$$\frac{{D_{\mathrm{min}}}m}{n} + 2 \ln n \le 0$$

which follows from

$$m \ge \frac{2 n \ln n}{{D_{\mathrm{min}}}} \le 4 \sqrt{n} \ln (n) =: m.$$

The last inequality used the Main technical theorem, which lower bounds ${D_{\mathrm{min}}}$. $\qedsymbol$