Min size of distinguishing sets

We spend the rest of this class with proving the Main technical theorem above.

Notation 3.1   Let $D(i) := \vert D(x,y)\vert$, where $i = c(x,y)$. $X_i = (\Omega; R_i)$. Let $X_i' = (\Omega; R_i \cup R_i^{-1})$ be the corresponding undirected graph.

Lemma 3.2   For $i \ge 1$, if $X_i'$ is not the complete graph, then $\mathop{\rm diam}\nolimits (\overline{X_i'}) = 2$.

Proof. There exist $x,y$ at distance $2$ in $\overline{X_i'}$, because there exist $x,z$ not adjacent in $\overline{X_i'}$, but $\overline{X_i'}$ is connected by primitivity, and so the third vertex of any minimal $x,z$-path is at distance $2$ from $x$.

Now take any $u,v \in \Omega$, not adjacent in $\overline{X_i'}$. Need to show: ${\mathrm {dist}}_{\overline{X_i'}} (u,v) \ge 2$. Need to show: $u,v$ have a common neighbor in $\overline{X_i'}$. $c(u,v) \in \{i, i^{-1}\}$. Implies # common neighbors of $u,v$ in $\overline{X_i'}$ is the same as for $x,y$. $\qedsymbol$

Lemma 3.3   $(\forall i \ge 1)( \rho_i \le n - 1 - \sqrt{n-1})$.

Proof. If $X_i'$ is the complete graph, then $\rho_i = (n-1)/2$ and we are done. Otherwise, use Lemma  and Exercise . $\qedsymbol$

Notation 3.4   We shal consider the average distinguishing number

$$\overline{D} = \frac{\sum_{x \ne y} \vert D(x,y)\vert}{n(n-1)}.$$

Also, let $\rho_{\max} := \max_i \rho_i$.

Lemma 3.5   $\overline{D} \ge n - \rho_{\max} \ge \sqrt{n-1} + 1 \sim \sqrt{n}$.

Proof. Count the number of triples $(x,y,z)$ such that $z \notin D(x,y)$. This means $c(x,z) = c(y,z) = \rho_i$ for some $i$. This is

$$n - \overline{D} = \frac{\sum_{i = 1}^{r-1} \rho_i (\rho_i - 1)}{n-1} \le \rho_{\max} \frac{\sum_{i=1}^{r-1} (\rho_i - 1)}{n-1} < \rho_{\max}.$$

$\qedsymbol$

Lemma 3.6   $D(i) \le {\mathrm {dist}}_{X_j'} (i) D(j)$.

Proof. Let $x_0, x_1, \dots, x_d$ be a in $X_j'$ path where $c(x_0, x_d) = i$. $D(x_0, x_d) \subseteq \cup_{i=1}^d D(x_{i-1},x_i)$. The size on the left side is $D(i)$; all stes on the right side have size $D(j)$. $\qedsymbol$

Notation 3.7   $\mathop{\rm diam}\nolimits (i):=\mathop{\rm diam}\nolimits (X_i').$

Corollary 3.8   $D(j) \ge \overline{D}/\mathop{\rm diam}\nolimits (j)$.

Proof. Need: $\overline{D} \le \mathop{\rm diam}\nolimits (j) D(j)$. Pick $i$ such that $D(i) \ge \overline{D}$. Then ${\mathrm {dist}}_{X_j'}(i) \le \mathop{\rm diam}\nolimits (X_j')=\mathop{\rm diam}\nolimits (j)$. $\qedsymbol$

Corollary 3.9   If $\mathop{\rm diam}\nolimits (i) = 2$ then $D(i) \gtrsim \sqrt{n}/2$.

Lemma 3.10 (Zemlyachenko)   If $\mathop{\rm diam}\nolimits (i) \ge 3$ then $D(i) \ge \rho_i/3$.

Proof. Let $x,y,z,w$ be a shortest path from $z$ to $w$ in $X_i'$. Let $X_i'(x) = \{$ neighbors of $x$ in color $i$ $\}$.

Claim 3.11   $X_i'(x) \subseteq D(x,w)$ and $D(i) \ge \vert D(x,w)\vert/3$. The Lemma is immediate from the following claim:

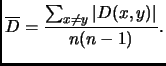
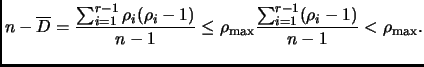
The claim is easy: if some $X_i'$-neighbor $u$ of $x$ did not distinguish $x$ from $w$ then $c(u,w)=c(u,x)=i^{\pm}$, so $x-u-w$ would be an $X_i'$-path of length 2, contradicting the assumption that ${\mathrm {dist}}_i(x,w)=3$. Now $\vert D(x,w)\vert\le 3D(i)$ by Lemma . $\qedsymbol$

Lemma 3.12   $(\forall h \ne 0)(\forall x)(x$    distinguishes at least $n-1$ pairs of color $h$$)$.

Proof. Let us construct a graph $H$ using the set $V = \{0, 1, \dots, r-1\}$ of colors as vertex set. Let $w(i,j)$ be the number of edges of color $h$ or $h^{-1}$ from $X_i(x)$ to $X_j(x)$. Put an edge between $i$ and $j$ if $w(i,j)\neq 0$; assign weight $w(i,j)$ to this edge. It follows from Exerciseconn-ex that if there is an $\{i,j\}$ edge then $w(i,j) \ge \max(\rho_i, \rho_j)$.

$H$ is a connected graph. This follows from the primitivity of $\ensuremath{\mathfrak{X}}$ (why?). Let $T$ be a spanning tree of $H$. Let us orient $T$ away from vertex (color) 0. $x$ distinguishes $\ge \tau$ edges of color $h$, where $\tau :=$ total weight of edges of $T$.

$$\tau = \sum_{i \to j} w(i,j) \ge \sum_{i \to j} \rho_j = \sum_{i=1}^{r-1} \rho_j = n-1.$$

$\qedsymbol$

Corollary 3.13   $D(i) \ge (n-1)/\rho_i$.

Proof. Count the triples $N = \left\vert\{(x,y,z) \mid c(x,y) = i, z \in D(x,y)\}\right\vert$ in two different ways.

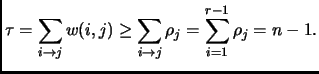
Count by $(x,y)$. The number of pairs $(x,y)$ such that $c(x,y) = i$ is $n \rho_i$. For each such pair, there are $D(i)$ choices for $z$. Thus,

$$N = n \rho_i D(i).$$

Now count by $z$. There are $n$ choices for $z$. Given $z$, there are at least $n-1$ pairs $(x,y)$ distinguished by $z$. Thus

$$N = n \rho_i D(i) \ge n(n-1),$$

and so

$$\rho_i D(i) \ge n-1.$$

$\qedsymbol$

Corollary 3.14   If $\mathop{\rm diam}\nolimits (i)\ge 3$ then $D(i) \gtrsim \sqrt{n/3}.$

Proof. Multiplying the expressions for $D(i)$ from Lemma  and Corollary , we get

$$D(i)^2 \ge \frac{\rho_i}{3}\cdot \frac{n-1}{\rho_i} = \frac{n-1}{3}.$$

Thus

$$D(i) \ge \sqrt{\frac{n-1}{3}} \sim \frac{\sqrt{n}}{\sqrt{3}}.$$

$\qedsymbol$

This result, combined with Corollary , completes the proof of the Main Theorem.

This proof is based on L. Babai: ``On the order of uniprimitive permutation groups,'' Annals of Math. 113 (1981), 553-568, as simplified by N. Zemlyachenko a year later.

Conjecture 3.15   For uniprimitive coherent configurations, $D_{\min} = \Omega(n - \rho_{\max})$. (Note that this is true for the average rather than the minimum size of distinguishing sets by Lemma .)

Another open question:

Conjecture 3.16   For primitive coherent configurations of rank $r\ge 4$, $D_{\min} = \Omega(n^{1 - 1/(r-1)}))$. Or at least $D_{\min} = \Omega(n^{1 - f(r)})$, where $f(r) \to 0$.

Note that the first statement is true for $r=2$.