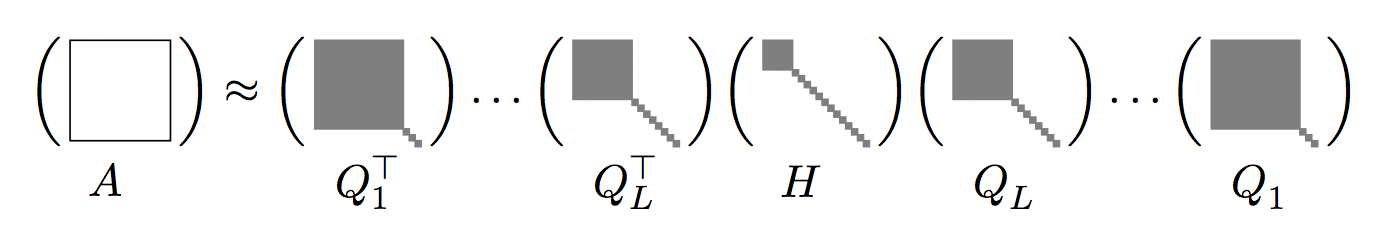|
|
Multiresolution matrix factorizations
Most commonly used matrix factorization algorithms, such as
eigendecomposition (PCA),
singular value decomposition (SVD),
or
non-negative matrix factorization (NMF) are inherently single-level algorithms.
For example, PCA decomposes a symmetric matrix \(A\) in the form
\[A=Q^\top\! D\,Q,\]
where \(Q\) is an orthogonal matrix and \(D\) is diagonal.
In general, the rows of \(Q\) are dense.
When \(A\) is a massive matrix coming from real world data, this becomes problematic, both from
the computational point of view and from the point of view of interpretability.
Our paper [P1] reformulated matrix factorization as a type of
multiresolution
analysis on a metric space, and used this connection to define a generic notion of
Multiresolution Matrix Factorization (MMF) of the form
\[A= Q_1^\top Q_2^\top\ldots Q_L^\top H Q_L\ldots Q_2 Q_1,\]
where the \(Q_1,Q_2,\ldots,Q_L\) orthogonal matrices are very sparse and \(H\) is close to
diagonal.
Subsequently, in [P2] we generalized the algorithm to a parallel setting and showed how
it can produce state-of-the-art results on matrix compression tasks
in close to linear time in the number of non-zeros [P3].
Currently, we are working on applying the MMF formalism to speed up
large scale numerical computations including Gaussian process inference [P5]
and solving linear systems [p6].
MMF is related to well established numerical analysis paradigms, such as
hierarchical matrices and
the fast multipole method.
Potentially, it can be used to accelerate a wide range of large linear algebra tasks.
However, this required writing a dedicated, high-performance, multicore implementation,
which we called pMMF, from scratch [S1]. The project necessitated
writing our own blocked sparse matrix library, which subsequently took on a life of its
own under the name Mondrian [S2].
Papers
[P1] R. Kondor, N. Teneva and V. Garg:
Multiresolution matrix factorization
(ICML 2014)
[paper]
[supplement]
[video]
[P2] R. Kondor, N. Teneva and P. K. Mudrakarta:
Parallel MMF: a multiresolution approach to matrix computation
(arXiv, July 2015)
[preprint]
[P3] N. Teneva, P. K. Mudrakarta and R. Kondor:
Multiresolution Matrix Compression
(AISTATS 2016)
(winner of notable student paper award)
[paper]
[P4] V. Ithapu, R. Kondor and V. Singh:
The Incremental Multiresolution Matrix Factorization Algorithm
(CVPR 2017)
[P5] Y. Ding, R. Kondor and J. Eskreis-Winkler:
Multiresolution kernel approximation for Gaussian process regression
(NIPS 2017)
[preprint]
[P6] P. K. Mudrakarta and R. Kondor:
A generic multiresolution preconditioner for sparse symmetric systems
[preprint]
Software
[S1] R. Kondor, N. Teneva and P. K. Mudrakarta:
pMMF: a high performance C++ library for parallel multiresolution matrix
factorization
[pMMF]
[S2] R. Kondor:
Mondrian: C++ parallel blocked matrix library
[Mondrian]
Events
I. Dhillon, R. Kondor, R. Nowak, M. O'Neil and N. Teneva:
Multiresolution Methods for Large Scale Learning
(NIPS 2015 workshop)
[schedule]
NIPS 2015
[videos]
|