


Next: Two common masks and
Up: Generating masks for volume
Previous: Generating masks for volume
Figure 4.3 demonstrated the use of a simple mask which
was used to measure the first derivative in one dimensional data.
This appendix will describe a process which produces masks for
measuring derivatives in one dimension, as well as how to generalize
one dimensional masks to measure first and second partial derivatives
in three dimensions19.
It was stated in Chapter 4 that reconstruction of a
continuous data value function between sample points in the volume
dataset is not necessary for measuring any of the quantities needed in
the histogram volume creation. Instead, discrete masks can be used to
measure the first and second partial derivatives which are needed for
the directional derivative calculations. Although we will not need to
explicitly reconstruct the data value anywhere, a simple way to derive
the necessary masks is through consideration of reconstruction filters
and convolution.
Given a sequence of sampled data points 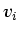 , the creation of a
continuous function which interpolates smoothly between them starts
with a train of delta function spikes at unit intervals, scaled
by the original data values:
, the creation of a
continuous function which interpolates smoothly between them starts
with a train of delta function spikes at unit intervals, scaled
by the original data values:
 |
(35) |
A continuous reconstructed signal can then be obtained by convolving
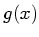 with a continuous kernel
with a continuous kernel 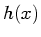 :
:
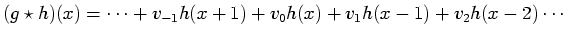 |
(36) |
Copies of the kernel are effectively placed at each sample point
and scaled by the corresponding data value. The first derivative of
the reconstructed function is easily computed, by the linearity of
taking derivatives:
Equation B.3 defines the infinite sum as the dot
product of two vectors, one listing the data values 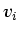 , and one
containing evaluations of the derivative of the kernel
, and one
containing evaluations of the derivative of the kernel 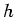 . If the
position
. If the
position 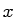 where we calculate the derivative of the reconstructed
function happens to be an integer
where we calculate the derivative of the reconstructed
function happens to be an integer 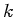 , we can express this as:
, we can express this as:
Assuming that the reconstruction kernel 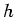 has finite support, there
can only be a finite number of non-zero values in the vector
has finite support, there
can only be a finite number of non-zero values in the vector
![$ \left[\cdots\,\!h'(2)\,h'(1)\,h'(0)\,h'(-1)\,h'(-2)\,\!\cdots\right]$](img247.gif) . The
finite vector containing all the non-zero values is a mask for
measuring the first derivative of regularly sampled data. Since most
reconstruction kernels are even functions (
. The
finite vector containing all the non-zero values is a mask for
measuring the first derivative of regularly sampled data. Since most
reconstruction kernels are even functions (
 ), the mask
will have an odd number of values, with
), the mask
will have an odd number of values, with 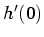 at the center
position. Equation B.4 shows how a mask is used:
after centering the mask at the data point of interest (
at the center
position. Equation B.4 shows how a mask is used:
after centering the mask at the data point of interest (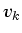 ), the
products between corresponding data and mask values are summed to
produce the final measurement.
), the
products between corresponding data and mask values are summed to
produce the final measurement.
Given any continuous reconstruction kernel 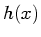 , we can evaluate its
first derivative at integer positions to generate a first derivative
mask. Of course, the first derivative has to exist at the integer
positions in order for this to be valid. As an example, we take the
Catmull-Rom cubic spline
, we can evaluate its
first derivative at integer positions to generate a first derivative
mask. Of course, the first derivative has to exist at the integer
positions in order for this to be valid. As an example, we take the
Catmull-Rom cubic spline 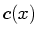 :
:
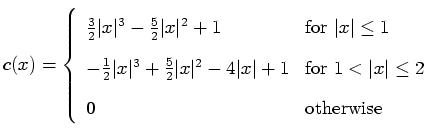 |
(39) |
One can verify that  is continuous; evaluating
is continuous; evaluating  at the
integers yields:
at the
integers yields:
![$\displaystyle [\cdots~~c'(2)~~c'(1)~~c'(0)~~c'(-1)~~c'(-2)~~\cdots] = [\cdots~~0~-0.5~~0~~0.5~~0~~\cdots]$](img254.gif) |
(40) |
Thus the Catmull-Rom kernel generates the first
derivative mask
![$ [-0.5~~0~~0.5]$](img64.gif) .
.
In the same way that first derivative masks were derived above, masks
for measuring the second derivative of regularly
sampled data can be created from a kernel 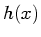 :
:
In this case, the second derivative of the reconstruction kernel must
exist at all integer locations for the mask to be valid. For
instance, by differentiating 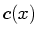 twice, one will
find that the Catmull-Rom kernel does not generate a second derivative mask
because its second derivative is discontinuous at
twice, one will
find that the Catmull-Rom kernel does not generate a second derivative mask
because its second derivative is discontinuous at 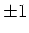 and
and  .
.
Footnotes
- ... dimensions19
- In Chapter 3 we
employed an abuse of terminology, using ``first derivative'' for
``first directional derivative along the gradient direction''. In this
section we return to the strict usage; ``first derivative'' means the
first derivative of a function of one variable (and likewise for a
second derivative).



Next: Two common masks and
Up: Generating masks for volume
Previous: Generating masks for volume
![]() , the creation of a
continuous function which interpolates smoothly between them starts
with a train of delta function spikes at unit intervals, scaled
by the original data values:
, the creation of a
continuous function which interpolates smoothly between them starts
with a train of delta function spikes at unit intervals, scaled
by the original data values:
![]() , we can evaluate its
first derivative at integer positions to generate a first derivative
mask. Of course, the first derivative has to exist at the integer
positions in order for this to be valid. As an example, we take the
Catmull-Rom cubic spline
, we can evaluate its
first derivative at integer positions to generate a first derivative
mask. Of course, the first derivative has to exist at the integer
positions in order for this to be valid. As an example, we take the
Catmull-Rom cubic spline ![]() :
:
![]() :
: