As was noted in Section 4.3, a common mask for
measuring the first derivative is
![]() , called the
``central difference'' method. The name arises from the derivative
approximation for a function
, called the
``central difference'' method. The name arises from the derivative
approximation for a function ![]() :
:
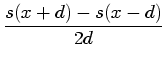 |
|||
 |
|||
![$\displaystyle [s(x-d)~~s(x)~~s(x+d)]^T~[\frac{1}{2d}~~0~-\frac{1}{2d}]$](img262.gif) |
(41) |
There is another simple and common mask for our second derivative
measurement, ![]() , sometimes called the ``second central
difference'' method. The name arises from the fact that the mask can
be derived by twice applying the method of central differences (now
with
, sometimes called the ``second central
difference'' method. The name arises from the fact that the mask can
be derived by twice applying the method of central differences (now
with ![]() ), as follows:
), as follows:
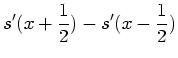 |
|||
| (42) |
There is an important theoretical question regarding the validity of
using these two masks in combination for the histogram volume
computation. Recall from Chapter 3 that we traced
along an ideal boundary to reveal a characteristic relationship
between the data value and its first and second derivatives, as
illustrated in Figure 3.8. The point
![]() was plotted for each position
was plotted for each position ![]() along the
boundary in order to form the three dimensional curve
which indicates the presence of a boundary. For such a case, the
boundary function
along the
boundary in order to form the three dimensional curve
which indicates the presence of a boundary. For such a case, the
boundary function ![]() studied was a continuous function with
analytically known derivatives, thus reconstruction was not an issue.
studied was a continuous function with
analytically known derivatives, thus reconstruction was not an issue.
However, when we are measuring derivatives of sampled data with masks, we are implicitly reconstructing the function. That is, the result of using a mask is mathematically equivalent to convolving the sample points with a continuous kernel and analytically finding the derivative of the reconstructed function. Thus, there is a basic incompatibility if there does not exist a reconstruction kernel which can generate both the first and second derivative masks being used. For such a case, the first and second derivatives measures would be based on different reconstructions of the same data. There is no guarantee that the relationship observed in Figure 3.8 will hold if the first and second derivatives are taken from entirely different functions.
It is therefore imperative that we find a reconstruction kernel which
generates
![]() and
and ![]() as its first and second
derivative masks, respectively. A piece-wise quintic polynomial
kernel
as its first and second
derivative masks, respectively. A piece-wise quintic polynomial
kernel ![]() was found which has all the necessary derivative
characteristics20:
was found which has all the necessary derivative
characteristics20:
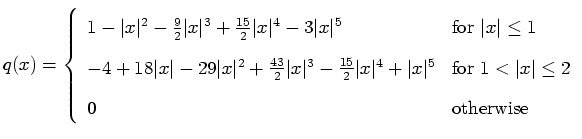 |
(43) |
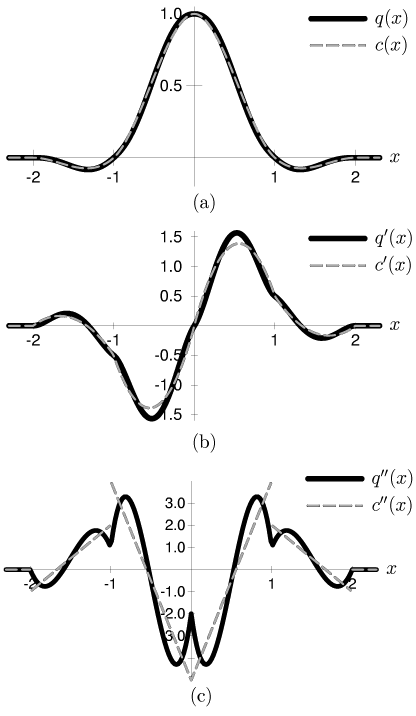 |
This quintic kernel was never implemented in the software for histogram volume generation, because it was never needed for any derivative measurements. Rather, its mere existence provides necessary justification for the approach taken in this thesis. It insures that there is some reconstruction of the sampled data which is consistent with the masks utilized for measuring derivatives. Equation B.3, and its analog for the second derivative, prove that the two masks we have chosen provide exact measures for the first and second derivatives of the data value as a continuous function of position, for the case where the data value was reconstructed with this quintic interpolation kernel.