


Next: Evaluating the performance of
Up: Generating masks for volume
Previous: Two common masks and
The two masks discussed thus far (
![$ [-0.5~~0~~0.5]$](img64.gif) for first
derivative and
for first
derivative and ![$ [1~-2~~1]$](img264.gif) for second derivative) are only
useful for measuring the derivatives of one dimensional data. These
are now generalized to create masks for measuring first and second
partial derivatives of sampled data in three dimensions.
for second derivative) are only
useful for measuring the derivatives of one dimensional data. These
are now generalized to create masks for measuring first and second
partial derivatives of sampled data in three dimensions.
Any reconstruction kernel 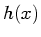 in one dimension can be trivially
extended to a separable kernel
in one dimension can be trivially
extended to a separable kernel
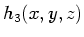 in three dimensions:
in three dimensions:
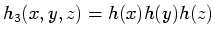 |
(44) |
The function representing the sampled data in a volume is a
three dimensional lattice of delta functions, scaled by the data
values  , where
, where 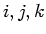 all range over the integers:
all range over the integers:
The reconstructed function
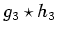 is a lattice of kernels scaled by
the data values:
is a lattice of kernels scaled by
the data values:
The partial derivatives of the reconstructed function are simple to
express:
As in the one dimensional case, these expressions can be rewritten
when the location at which the derivative is taken is a point
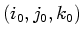 on the integer lattice:
on the integer lattice:
In this form, the expressions for the partial derivatives of the
reconstructed function are a close analog to
Equation B.4, the formulation of one dimensional
derivative masks.
Whereas the one dimensional mask was a vector of evaluations of
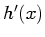 ,
we now have a three dimensional lattice of evaluations of a partial
derivative of
,
we now have a three dimensional lattice of evaluations of a partial
derivative of 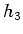 . These are the masks for derivative measurement
in three dimensions. For example, the mask for calculating the first
partial derivative along the
. These are the masks for derivative measurement
in three dimensions. For example, the mask for calculating the first
partial derivative along the 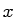 axis,
axis,
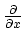 , is the
lattice of values
, is the
lattice of values
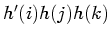 , where
, where 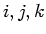 all range over
the integers. The mask for the second mixed partial derivative along
the
all range over
the integers. The mask for the second mixed partial derivative along
the 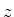 and
and 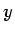 axes,
axes,
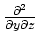 , is the lattice of
values
, is the lattice of
values
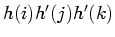 . As before, we assume the kernel
. As before, we assume the kernel 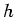 has
finite support, thus there are only a finite number of non-zero values
in the masks. Figure B.2 depicts the masks for
has
finite support, thus there are only a finite number of non-zero values
in the masks. Figure B.2 depicts the masks for
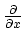 and
and
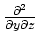 .
.
Figure B.2:
Two examples of masks for volume derivative measurement
![\begin{figure}
\setcounter {subfigure}{0}
\psfrag{zeqnegone}[lb]{\hspace{0pt}...
...}}}
\epsfig {figure=eps/threedmask.eps,
width=0.4\textwidth}}
}
\end{figure}](img303.gif) |
Even though these masks have an obvious three dimensional structure,
the mathematics of their application is still that of a dot product:
the mask is centered at the sample point of interest, and the products
between corresponding data and mask values are summed to produce the
final measurement. Having decided on the quintic kernel 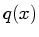 for
all mask generation, Equations B.11 can be
used to generate
for
all mask generation, Equations B.11 can be
used to generate
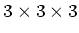 masks for all the partial
derivatives needed for any of the directional derivative measures.
masks for all the partial
derivatives needed for any of the directional derivative measures.



Next: Evaluating the performance of
Up: Generating masks for volume
Previous: Two common masks and
![]() for first
derivative and
for first
derivative and ![]() for second derivative) are only
useful for measuring the derivatives of one dimensional data. These
are now generalized to create masks for measuring first and second
partial derivatives of sampled data in three dimensions.
for second derivative) are only
useful for measuring the derivatives of one dimensional data. These
are now generalized to create masks for measuring first and second
partial derivatives of sampled data in three dimensions.
![]() in one dimension can be trivially
extended to a separable kernel
in one dimension can be trivially
extended to a separable kernel
![]() in three dimensions:
in three dimensions:
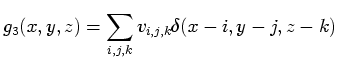
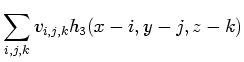
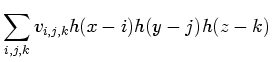
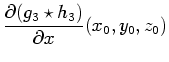
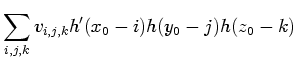

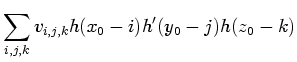
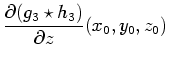
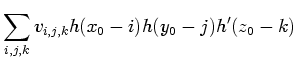
![]() ,
we now have a three dimensional lattice of evaluations of a partial
derivative of
,
we now have a three dimensional lattice of evaluations of a partial
derivative of ![]() . These are the masks for derivative measurement
in three dimensions. For example, the mask for calculating the first
partial derivative along the
. These are the masks for derivative measurement
in three dimensions. For example, the mask for calculating the first
partial derivative along the ![]() axis,
axis,
![]() , is the
lattice of values
, is the
lattice of values
![]() , where
, where ![]() all range over
the integers. The mask for the second mixed partial derivative along
the
all range over
the integers. The mask for the second mixed partial derivative along
the ![]() and
and ![]() axes,
axes,
![]() , is the lattice of
values
, is the lattice of
values
![]() . As before, we assume the kernel
. As before, we assume the kernel ![]() has
finite support, thus there are only a finite number of non-zero values
in the masks. Figure B.2 depicts the masks for
has
finite support, thus there are only a finite number of non-zero values
in the masks. Figure B.2 depicts the masks for
![]() and
and
![]() .
.