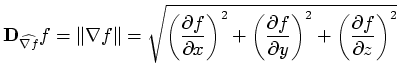 |
(46) |
It is relatively easy to perform an analytical Fourier analysis of an individual mask in order to find its frequency response, which is useful information for determining how the mask will respond to ideal boundaries of various thicknesses[BLM96]. But what is more relevant to the problem of histogram volume calculation is determining the frequency response of the directional derivative measure as a whole. Unfortunately, due to the complexity of the directional derivative formulas in Equations C.2, C.3, and C.5, the task is outside the scope of this thesis.
Instead, we evaluate the derivative measures by using them to analyze
synthetic volumes containing a range of boundary
thicknesses. Specifically, we create a synthetic volume for every
boundary thickness between ![]() and
and ![]() , at increments of
, at increments of ![]() .
The synthetic volumes contain only planar boundaries, so we should
keep in mind that the Laplacian second derivative measure will be
uncharacteristically accurate, since it gives a correct directional
derivative measure only for planar boundaries21. All the synthetic volumes were
.
The synthetic volumes contain only planar boundaries, so we should
keep in mind that the Laplacian second derivative measure will be
uncharacteristically accurate, since it gives a correct directional
derivative measure only for planar boundaries21. All the synthetic volumes were
![]() in size. One subtle feature of the volumes was that the
boundary planes were purposely not axis aligned. This created more
variation in the spatial relationship between the boundary and the
sampling grid, which led to a better distribution of voxels along the
curves in the scatterplots. Also, to maximize the number of voxels
which accumulate along the curves in the scatterplots, multiple
boundaries were created in each volume. By varying the spacing
between boundaries in proportion to the boundary thickness, we
maintain an approximately constant accumulation of hits along the
scatterplot curves.
in size. One subtle feature of the volumes was that the
boundary planes were purposely not axis aligned. This created more
variation in the spatial relationship between the boundary and the
sampling grid, which led to a better distribution of voxels along the
curves in the scatterplots. Also, to maximize the number of voxels
which accumulate along the curves in the scatterplots, multiple
boundaries were created in each volume. By varying the spacing
between boundaries in proportion to the boundary thickness, we
maintain an approximately constant accumulation of hits along the
scatterplot curves.
![\begin{figure}
\setcounter {subfigure}{0}\centering {
\subfigure[]{
\epsfig {f...
...ure=eps6/bounds/bounds-6.00-rend.high.eps, width=0.4\textwidth} }
}
\end{figure}](img313.gif) |
Three histogram volumes are then calculated for each synthetic volume.
While the gradient magnitude is always used for the first directional
derivative measure, each of the three different second directional
derivative measures are used once. All histogram volumes were
calculated at a resolution of ![]() . These histogram volumes are
then projected to create scatterplots which we can visually compare in
order to gain a qualitative understanding of how the derivative
measures perform for a variety of boundary thicknesses. Recall from
Section 4.3 that one important issue in
histogram volume calculation is the range of derivative values that
should be included on the first and second derivative axes of the
histogram volume. In the analysis of these synthetic volumes, for
each boundary thickness, the full range of the first and second
derivative values which occur within the ideal boundary was
calculated, and the range of derivative values to be included in the
histogram volume was set to 120% of this. This provides the basis
for qualitative evaluation of the derivative measures: by comparing
the ideal versus actual sizes of the curves in the scatterplots, we
get a sense of how the derivative measures respond to boundaries of a
given thickness.
. These histogram volumes are
then projected to create scatterplots which we can visually compare in
order to gain a qualitative understanding of how the derivative
measures perform for a variety of boundary thicknesses. Recall from
Section 4.3 that one important issue in
histogram volume calculation is the range of derivative values that
should be included on the first and second derivative axes of the
histogram volume. In the analysis of these synthetic volumes, for
each boundary thickness, the full range of the first and second
derivative values which occur within the ideal boundary was
calculated, and the range of derivative values to be included in the
histogram volume was set to 120% of this. This provides the basis
for qualitative evaluation of the derivative measures: by comparing
the ideal versus actual sizes of the curves in the scatterplots, we
get a sense of how the derivative measures respond to boundaries of a
given thickness.
Figures C.3, C.4, and
C.5 show the results of this analysis. Each
line of the table corresponds to one boundary thickness (![]() ),
which is written in the first column. In the next column are slices
of the datasets analyzed. After the slice, from left to right, each
row contains the
),
which is written in the first column. In the next column are slices
of the datasets analyzed. After the slice, from left to right, each
row contains the ![]() versus
versus ![]() scatterplot, followed by the
three
scatterplot, followed by the
three ![]() versus
versus ![]() scatterplots, using the different second
derivative measures: gradient of gradient magnitude (from
Equation C.2), Hessian (Equation C.3), and
Laplacian (Equation C.5). The tops of the scatterplot
columns are labeled to indicate which derivative has been measured and
how. The scatterplots are turned on their sides (rotated 90 degrees
clockwise from their usual presentation) to facilitate comparison of
the peak amplitude in the curves across different thicknesses. Also, a
thin dashed line indicates where the peak of the scatterplot curve
would be in an ideal measurement. To serve as a basis for comparison,
Figure C.2 shows the two ideal scatterplots in the new
orientation.
scatterplots, using the different second
derivative measures: gradient of gradient magnitude (from
Equation C.2), Hessian (Equation C.3), and
Laplacian (Equation C.5). The tops of the scatterplot
columns are labeled to indicate which derivative has been measured and
how. The scatterplots are turned on their sides (rotated 90 degrees
clockwise from their usual presentation) to facilitate comparison of
the peak amplitude in the curves across different thicknesses. Also, a
thin dashed line indicates where the peak of the scatterplot curve
would be in an ideal measurement. To serve as a basis for comparison,
Figure C.2 shows the two ideal scatterplots in the new
orientation.
![\begin{figure}
\setcounter {subfigure}{0}\psfrag{g}[tl]{\hspace{2pt}\raisebox{...
... \epsfig {figure=eps6/bounds/idealhv.eps, width=0.25\textwidth} }
}
\end{figure}](img314.gif) |
The first thing to notice about the scatterplots in
Figures C.3, C.4, and
C.5 is that for small thicknesses (around 1.00),
none of the derivative measures' responses were very high. Besides
being distorted in shape compared to the ideal, the scatterplot curves
are compressed towards the ![]() axis. This is an important
consideration when analyzing volumes with sharp transitions between
material regions. Because the histogram volume will contain a
somewhat distorted measure of the boundaries, the
axis. This is an important
consideration when analyzing volumes with sharp transitions between
material regions. Because the histogram volume will contain a
somewhat distorted measure of the boundaries, the ![]() ,
, ![]() , and
, and
![]() calculations will also be distorted, and there will be a
mismatch between the user-specified boundary function
calculations will also be distorted, and there will be a
mismatch between the user-specified boundary function ![]() and the
actual opacity assigned to the boundaries in the volume by the opacity
function created from our algorithm. As was done with the turbine
blade dataset (Section 6.1), it may be beneficial to
slightly blur the volume as a pre-process, if the resulting slight
loss of detail is tolerable.
and the
actual opacity assigned to the boundaries in the volume by the opacity
function created from our algorithm. As was done with the turbine
blade dataset (Section 6.1), it may be beneficial to
slightly blur the volume as a pre-process, if the resulting slight
loss of detail is tolerable.
The row for thickness 2.66 at the bottom of
Figure C.3 shows the typical relationship
between the three second derivative measures. The measure based on
![]() gives the smallest amplitude response to the
boundary, while the measures based on
gives the smallest amplitude response to the
boundary, while the measures based on
![]() and
and
![]() are closer to the ideal, and are about equal. The more noticeable
difference between the three measures is the amount of spread in the
range of derivative values at a single data value. The curve from the
are closer to the ideal, and are about equal. The more noticeable
difference between the three measures is the amount of spread in the
range of derivative values at a single data value. The curve from the
![]() measure is very coherent, but the
measure is very coherent, but the
![]() curve is more dispersed, and the
curve is more dispersed, and the
![]() curve is even more so.
curve is even more so.
The dispersion of the scatterplot curves is a result of
quantization noise, the error introduced by representing a signal's
values with fixed point instead of floating point precision. All the
synthetic volumes generated for this analysis contained only 8-bit
quantities. As a result, the error in the signal value (as stored in
the synthetic dataset) is on average one half of ![]() , or
, or ![]() .
This amount is small relative to the changes in data value within
sharp boundaries, but it is a greater percentage of the change in data
value within more blurred boundaries. Thus, as the boundaries become
more blurred, the quantization noise will become more and more
prominent in a derivative measurement. Also, since second derivative
measures are by nature more sensitive to noise than first derivative
measures, the effect of quantization is always more evident in the
.
This amount is small relative to the changes in data value within
sharp boundaries, but it is a greater percentage of the change in data
value within more blurred boundaries. Thus, as the boundaries become
more blurred, the quantization noise will become more and more
prominent in a derivative measurement. Also, since second derivative
measures are by nature more sensitive to noise than first derivative
measures, the effect of quantization is always more evident in the
![]() scatterplots than in the one for
scatterplots than in the one for ![]() .
.
The collection of scatterplots as a whole hints at a fundamental
relationship between the bit depth of the data, the boundary
thickness, and the derivative measures' robustness against
quantization noise, as governed by the mathematical properties
of the derivative measures. A thorough exploration of this
relationship would be vital to the design of higher quality derivative
measures, but for the time being we choose amongst the ones already
implemented. As can be seen in Figures C.4 and
C.5, the second derivative measures can be
ordered by their sensitivity to quantization noise:
![]() ,
,
![]() , and then
, and then
![]() . By the time the
thickness has reached 6.00 or higher, the
. By the time the
thickness has reached 6.00 or higher, the
![]() curve has
become so dispersed as to be unrecognizable, while even at thickness
8.00 the
curve has
become so dispersed as to be unrecognizable, while even at thickness
8.00 the
![]() curve is still reasonably coherent.
Despite this, the
curve is still reasonably coherent.
Despite this, the
![]() measure is less accurate than
the other two measures, since its curve is always further from the
ideal size than the others. Given the trade-offs between the three
measures in terms of quantization noise, accuracy, and computational
cost, we have generally adopted the Hessian-based second derivative
measure as the standard.
measure is less accurate than
the other two measures, since its curve is always further from the
ideal size than the others. Given the trade-offs between the three
measures in terms of quantization noise, accuracy, and computational
cost, we have generally adopted the Hessian-based second derivative
measure as the standard.