


Next: Comparison with Levoy's two
Up: Opacity function generation
Previous: Opacity functions of data
Opacity functions of data value and gradient magnitude
The opacity functions considered so far have assigned opacity based on
data value alone. Value-based opacity functions are easy to implement
and facilitate simple and efficient rendering algorithms. Higher
quality renderings can sometimes be obtained, however, if the opacity
is assigned as a function of both data value and gradient
magnitude. We term these two dimensional opacity
functions. Defining these two dimensional opacity functions by hand is
especially challenging because there are even more degrees of freedom
than in one dimensional, value-based opacity functions. Fortunately,
the ideas presented so far easily generalize to allow semi-automatic
generation of two dimensional opacity functions.
Analogous to the definition of 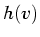 , we define
, we define 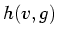 to be
the average second derivative over all locations where the data value is
to be
the average second derivative over all locations where the data value is
 and the gradient magnitude is
and the gradient magnitude is  . As before, this information
can be extracted from the histogram volume, as illustrated in Figure 5.7.
. As before, this information
can be extracted from the histogram volume, as illustrated in Figure 5.7.
Figure 5.7:
Calculating 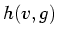 from the histogram volume. As in
Figure 5.3, a histogram volume schematic is shown, but
now a single scanline of the volume is extracted where data value is
from the histogram volume. As in
Figure 5.3, a histogram volume schematic is shown, but
now a single scanline of the volume is extracted where data value is
 and the first derivative is
and the first derivative is 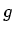 . The accumulation of sample
points along this line is shown as a diffuse dark region. The
location of the center of the region is
. The accumulation of sample
points along this line is shown as a diffuse dark region. The
location of the center of the region is 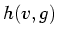 .
.
![\begin{figure}
\psfrag{f0pa}[lc]{\hspace{2pt}\raisebox{0pt}{\scalebox {0.85}{$f(...
...}
\centering {
\epsfig {file=eps/findhvg.eps, width=0.9\textwidth}}
\end{figure}](img137.gif) |
For data value  and first derivative
and first derivative 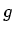 there is a one dimensional
histogram which records the distribution of second derivative values
for those sample points which had both data value
there is a one dimensional
histogram which records the distribution of second derivative values
for those sample points which had both data value  and gradient
magnitude
and gradient
magnitude 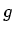 .
. 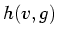 is the average of the distribution of second
derivative values. In direct emulation of
Equations 5.10 and 5.11, we define a
new position function, and from that an opacity function:
is the average of the distribution of second
derivative values. In direct emulation of
Equations 5.10 and 5.11, we define a
new position function, and from that an opacity function:
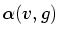 is defined to be zero for those
is defined to be zero for those  pairs which never
occur in the volume.
pairs which never
occur in the volume.  is calculated exactly the same as before,
using Equation 5.8. But whereas before a position
was found for each data value, we are now finding position for every
combination of data value and gradient magnitude. The resulting
opacity function is thus two dimensional instead of one dimensional.
As in the case of value-based opacity functions, the method presented
here will generate two dimensional opacity functions which make all
detected boundaries opaque. A simple ``lasso'' tool could then be used
to select different regions in the two dimensional opacity function to
render one boundary at a time.
is calculated exactly the same as before,
using Equation 5.8. But whereas before a position
was found for each data value, we are now finding position for every
combination of data value and gradient magnitude. The resulting
opacity function is thus two dimensional instead of one dimensional.
As in the case of value-based opacity functions, the method presented
here will generate two dimensional opacity functions which make all
detected boundaries opaque. A simple ``lasso'' tool could then be used
to select different regions in the two dimensional opacity function to
render one boundary at a time.
To demonstrate the generation of two dimensional opacity functions,
consider the dataset first seen in Figure 4.5,
containing two concentric cylindrical shells each at distinct data
values.
Figure 5.8:
Precursors to the
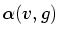 calculation for nested cylindrical
shells. (a) shows a cross-section of the data, labeling the regions
of the three distinct data values. The color image in (b) represents
the
calculation for nested cylindrical
shells. (a) shows a cross-section of the data, labeling the regions
of the three distinct data values. The color image in (b) represents
the 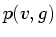 function that was computed from
Equation 5.12. The values of
function that was computed from
Equation 5.12. The values of 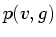 are shown with
a colormap, the legend of which is shown. In (c) a simple boundary
emphasis function is plotted.
are shown with
a colormap, the legend of which is shown. In (c) a simple boundary
emphasis function is plotted.
![\begin{figure}
\setcounter {subfigure}{0}
\psfrag{v1}[tc]{\hspace{0pt}\rai...
...h}{\epsfig{figure=eps/twosph-bemph3.eps,
width=0.3\textwidth}}}}
}
\end{figure}](img143.gif) |
As can be seen in Figure 5.8(a), this dataset is
similar to the nested spheres used in the previous section, in that it
has a background value 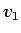 , and two material values
, and two material values 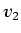 and
and 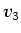 .
However, here the
.
However, here the 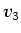 region shares a boundary not just with the
region shares a boundary not just with the
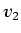 region, but also with the
region, but also with the 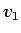 background region. If one
wanted to visualize just the
background region. If one
wanted to visualize just the 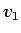 -
-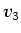 boundary with a value-based
opacity function, the opacity function would have to make the values
halfway between
boundary with a value-based
opacity function, the opacity function would have to make the values
halfway between 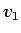 and the
and the 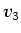 opaque. Unfortunately, these are
precisely the values near
opaque. Unfortunately, these are
precisely the values near 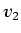 , the value within the outer
cylindrical shell. Thus the outer shell would obscure the
, the value within the outer
cylindrical shell. Thus the outer shell would obscure the
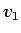 -
-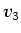 boundary in any rendering. For this reason,
one dimensional opacity functions are not sufficient to selectively
render the boundaries in this dataset.
boundary in any rendering. For this reason,
one dimensional opacity functions are not sufficient to selectively
render the boundaries in this dataset.
Figure 5.8(b) shows 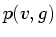 as calculated from
Equation 5.12, with the aid of a colormap which is
orange for positive values, blue for negative values, and purple in
between the two extremes. Additionally, there is a small band of dark
gray for values very close to zero. Where
as calculated from
Equation 5.12, with the aid of a colormap which is
orange for positive values, blue for negative values, and purple in
between the two extremes. Additionally, there is a small band of dark
gray for values very close to zero. Where 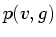 is undefined, the
image is white. Note that as one moves along the arches from left to
right,
is undefined, the
image is white. Note that as one moves along the arches from left to
right, 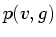 changes from negative to positive, hitting zero at the
peak of the arches. This is closely analogous to the plot of
changes from negative to positive, hitting zero at the
peak of the arches. This is closely analogous to the plot of 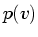 for the nested spheres (Figure 5.4(f)) in the previous
section, where position went from negative to positive as we moved up
the data value axis. The position information
for the nested spheres (Figure 5.4(f)) in the previous
section, where position went from negative to positive as we moved up
the data value axis. The position information 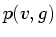 is then fed
into a simple boundary emphasis function
is then fed
into a simple boundary emphasis function 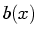 , shown in
Figure 5.8(c). Even though the user-specified
, shown in
Figure 5.8(c). Even though the user-specified 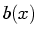 is still a simple function of one variable, it facilitates the
creation of a two dimensional opacity function.
is still a simple function of one variable, it facilitates the
creation of a two dimensional opacity function.
Figure 5.9:
Renderings of nested cylinders and corresponding
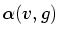 . (a)
shows the two dimensional opacity function
. (a)
shows the two dimensional opacity function
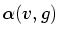 initially
generated from Equation 5.13 and a simple
initially
generated from Equation 5.13 and a simple 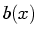 .
As with the scatterplots, the data value is on the horizontal axis,
and gradient magnitude on the vertical. Black areas represent
transparency; white is fully opaque. All three boundaries are visible
in the corresponding rendering. By zeroing out areas in
.
As with the scatterplots, the data value is on the horizontal axis,
and gradient magnitude on the vertical. Black areas represent
transparency; white is fully opaque. All three boundaries are visible
in the corresponding rendering. By zeroing out areas in
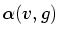 ,
other boundaries can be removed with ease, as seen in (b) and (c).
,
other boundaries can be removed with ease, as seen in (b) and (c).
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{avg}[lc]{\hs...
...figure=eps/weeramp.eps,
width=0.3\textwidth}}
\end{tabular} }}
}
\end{figure}](img144.gif) |
The relationship between the two dimensional opacity function and the
final rendering is shown in Figure 5.9. The
initial opacity function calculated with
Equation 5.13 (and the 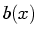 plotted in
Fig. 5.8(c)) is shown at the bottom of
Figure 5.9(a). As there were three boundaries
recorded in the histogram volume, there are three bright regions in the
opacity function, one for each boundary. To allow seeing internal
structure, none of the boundaries have been rendered fully opaque.
When we remove one of the regions of high opacity from
plotted in
Fig. 5.8(c)) is shown at the bottom of
Figure 5.9(a). As there were three boundaries
recorded in the histogram volume, there are three bright regions in the
opacity function, one for each boundary. To allow seeing internal
structure, none of the boundaries have been rendered fully opaque.
When we remove one of the regions of high opacity from
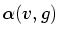 (Figure 5.9(b)), the corresponding boundary
disappears from the rendering. In Fig. 5.9(b), what
remains is the surface of the inner cylindrical shell. Since this
object has boundaries with both the background and the lower object
value, we can selectively render one or the other part of the surface,
as demonstrated in Fig 5.9(c).
(Figure 5.9(b)), the corresponding boundary
disappears from the rendering. In Fig. 5.9(b), what
remains is the surface of the inner cylindrical shell. Since this
object has boundaries with both the background and the lower object
value, we can selectively render one or the other part of the surface,
as demonstrated in Fig 5.9(c).
Though a contrived example, this serves to demonstrate the power of
the method for two dimensional opacity function generation. In the
one dimensional case, each detected boundary was marked by a spike in
the opacity function of data value. Here, each detected boundary is
marked by a bright spot in the two dimensional opacity function. This
immediately gives the user a feel for what types of boundaries occur
in the volume. By making only the middle of boundaries opaque, the
different significant regions in the opacity function can be easily
differentiated from each other by the user, and then edited to control
which boundaries are rendered. Other examples of the effectiveness of
this technique in generating two dimensional opacity functions are
given in Chapter 6.



Next: Comparison with Levoy's two
Up: Opacity function generation
Previous: Opacity functions of data
![]() , we define
, we define ![]() to be
the average second derivative over all locations where the data value is
to be
the average second derivative over all locations where the data value is
![]() and the gradient magnitude is
and the gradient magnitude is ![]() . As before, this information
can be extracted from the histogram volume, as illustrated in Figure 5.7.
. As before, this information
can be extracted from the histogram volume, as illustrated in Figure 5.7.
![\begin{figure}
\psfrag{f0pa}[lc]{\hspace{2pt}\raisebox{0pt}{\scalebox {0.85}{$f(...
...}
\centering {
\epsfig {file=eps/findhvg.eps, width=0.9\textwidth}}
\end{figure}](img137.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\psfrag{v1}[tc]{\hspace{0pt}\rai...
...h}{\epsfig{figure=eps/twosph-bemph3.eps,
width=0.3\textwidth}}}}
}
\end{figure}](img143.gif)
![]() as calculated from
Equation 5.12, with the aid of a colormap which is
orange for positive values, blue for negative values, and purple in
between the two extremes. Additionally, there is a small band of dark
gray for values very close to zero. Where
as calculated from
Equation 5.12, with the aid of a colormap which is
orange for positive values, blue for negative values, and purple in
between the two extremes. Additionally, there is a small band of dark
gray for values very close to zero. Where ![]() is undefined, the
image is white. Note that as one moves along the arches from left to
right,
is undefined, the
image is white. Note that as one moves along the arches from left to
right, ![]() changes from negative to positive, hitting zero at the
peak of the arches. This is closely analogous to the plot of
changes from negative to positive, hitting zero at the
peak of the arches. This is closely analogous to the plot of ![]() for the nested spheres (Figure 5.4(f)) in the previous
section, where position went from negative to positive as we moved up
the data value axis. The position information
for the nested spheres (Figure 5.4(f)) in the previous
section, where position went from negative to positive as we moved up
the data value axis. The position information ![]() is then fed
into a simple boundary emphasis function
is then fed
into a simple boundary emphasis function ![]() , shown in
Figure 5.8(c). Even though the user-specified
, shown in
Figure 5.8(c). Even though the user-specified ![]() is still a simple function of one variable, it facilitates the
creation of a two dimensional opacity function.
is still a simple function of one variable, it facilitates the
creation of a two dimensional opacity function.
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{avg}[lc]{\hs...
...figure=eps/weeramp.eps,
width=0.3\textwidth}}
\end{tabular} }}
}
\end{figure}](img144.gif)