


Next: Opacity function generation
Up: Histogram volume calculation
Previous: Implementation
Subsections
Histogram volume inspection
In Section 4.2 we stated that if there are
boundaries in the original dataset that conform to our boundary model,
there should be curves like that of Figure 3.8 in the
histogram volume. We now verify this fact by looking at histogram
volumes from datasets known to contain boundaries. Although one may
be tempted to volume render the histogram volume from various
viewpoints in order to visualize its content, this turns out to be
difficult and unrevealing due to the speckled nature of the histogram
volume. A better way to visualize histogram volumes is to project
them along either the first or second derivative axis. This produces
two dimensional scatterplots of data value versus first derivative, or
data value versus second derivative, as were seen in
4.2(c).
Figure 4.4:
Dataset cross-section and histogram scatterplots for cylinder.
A cross-section of the dataset is shown in (a), illustrating that there is
only one boundary in the volume, with the two material values tagged
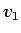 and
and 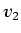 . (b) is a projection of the histogram volume
showing the relationship between
. (b) is a projection of the histogram volume
showing the relationship between  and
and 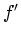 ; (c) likewise shows
the relationship between
; (c) likewise shows
the relationship between  and
and 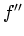 . In both (b) and (c) the
data values
. In both (b) and (c) the
data values 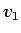 and
and 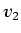 are indicated on the
are indicated on the 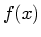 axis.
axis.
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...g {figure=eps/cyl-th3.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img72.gif) |
We start by looking at synthetically generated datasets, beginning
with a simple dataset-- a cylinder like that of
Figure 3.4.
Figure 4.4(a) shows the cylinder in cross-section.
The histogram volume is then projected along the 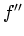 axis to produce
a
axis to produce
a 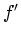 versus
versus  scatterplot (Figure 4.4(b)) and along
the
scatterplot (Figure 4.4(b)) and along
the 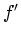 axis to produce a
axis to produce a 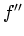 versus
versus  scatterplot
(Figure 4.4(c)). In these scatterplot images, the data
value and its derivatives are oriented on the axes as they were in
Figure 4.2 to facilitate comparison. The darkness in
the scatterplots encodes the number of hits for a given (value,
gradient) pair-- the darker, the more hits. These scatterplots
conform closely to the curves that were seen in
Figure 4.2(a).
scatterplot
(Figure 4.4(c)). In these scatterplot images, the data
value and its derivatives are oriented on the axes as they were in
Figure 4.2 to facilitate comparison. The darkness in
the scatterplots encodes the number of hits for a given (value,
gradient) pair-- the darker, the more hits. These scatterplots
conform closely to the curves that were seen in
Figure 4.2(a).
As a second verification of our discussion, and as a demonstration
of the utility of the histogram volume to capture information about
objects' boundaries, we analyze a second synthetic dataset which
contains two materials distinct from the background.
Figure 4.5:
Dataset cross-section and histogram scatterplots for two material
cylinder. (a) is a cross-section of the data, (b) and (c) are
projections of the histogram volume showing 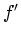 versus
versus  and
and 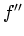 versus
versus  , respectively. As there are three distinct values
, respectively. As there are three distinct values 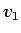 ,
,
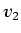 ,
, 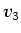 in the dataset, with a boundary between each pair of
values, there are three curves in the scatterplots. The curves start
and end at the three data values
in the dataset, with a boundary between each pair of
values, there are three curves in the scatterplots. The curves start
and end at the three data values 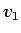 ,
, 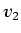 , and
, and 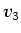 , indicated on
the
, indicated on
the 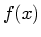 axis.
axis.
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...{figure=eps/shell-th3.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img74.gif) |
Figure 4.5(a) shows the dataset in cross-section.
An outer shell with an intermediate data value (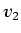 ) surrounds an
inner shell with a high data value (
) surrounds an
inner shell with a high data value (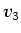 ), and the core is the same
as the background value (
), and the core is the same
as the background value (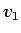 ). Hence there are three boundaries.
This fact is also revealed in Figure 4.5(b) and
Figure 4.5(c) by the presence of three curves, one for
each boundary.
). Hence there are three boundaries.
This fact is also revealed in Figure 4.5(b) and
Figure 4.5(c) by the presence of three curves, one for
each boundary.
Now we look at histogram volumes for real datasets, starting with a
CT scan of a turbine blade6. As the blade is made of a single kind
of metal, we would expect to find a single boundary indicated by
the histogram volume or its projections.
Figure 4.6:
Dataset cross-section and histogram scatterplots for turbine blade.
The cross-section (a) shows that there is only one boundary. This
is supported by the scatterplots of 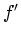 versus
versus  (b) and
(b) and 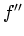 versus
versus  (c).
(c).
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...g {figure=eps/blade-crop-b1.vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img75.gif) |
Figure 4.6 illustrates this. The two large dark
spots in the histogram projections arise from the large regions of
nearly constant value within the air or the metal. The curves are the
result of the boundary between the two, and their shape matches those
of Figure 4.4, indicating a good match between the
properties of an ideal boundary, and the actual properties of this
dataset. Another exemplary dataset is the engine block CT scan first
seen in Figure 1.1.
Figure 4.7:
Dataset cross-section and histogram scatterplots for engine block.
The cross-section in (a) shows that there are three kind of material,
tagged with 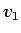 , and
, and 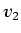 , and
, and 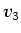 . We can also see that like
the nested cylinders in Fig. 4.5, there is a boundary
between every pair of values. Though not especially clear, the
scatterplots of
. We can also see that like
the nested cylinders in Fig. 4.5, there is a boundary
between every pair of values. Though not especially clear, the
scatterplots of 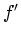 versus
versus  (b) and
(b) and 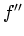 versus
versus  (c) support
this.
(c) support
this.
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...ps/engine-crop-b1-rsmp.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img76.gif) |
Figure 4.7 shows a dataset slice and the two
scatterplots for the engine dataset. The most prominent boundary
curve is for the transition from the background value (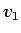 ) to the
intermediate value (
) to the
intermediate value (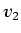 ), which comprises the majority of the engine
block's interior. A fainter curve is discernible between the
intermediate value (
), which comprises the majority of the engine
block's interior. A fainter curve is discernible between the
intermediate value (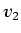 ) and a high value (
) and a high value (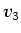 ). Finally, a very
faint and diffuse curve is evident arching over the other two
boundaries, spanning from the background value (
). Finally, a very
faint and diffuse curve is evident arching over the other two
boundaries, spanning from the background value (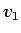 ) to the highest
value (
) to the highest
value (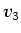 ). It makes sense that these last two curves should be so
much fainter than the first, because, as we can tell from looking at
the image of the dataset cross-section, the surface area of the
boundary between the background value and the intermediate value is
much greater than the area of either of the other two boundaries.
Thus, there are fewer voxels contributing to corresponding curves on
the scatterplot.
). It makes sense that these last two curves should be so
much fainter than the first, because, as we can tell from looking at
the image of the dataset cross-section, the surface area of the
boundary between the background value and the intermediate value is
much greater than the area of either of the other two boundaries.
Thus, there are fewer voxels contributing to corresponding curves on
the scatterplot.
Figure 4.8:
Dataset cross-section and histogram scatterplots for neuron. The
cross-section of the data (a) shows that there is no one constant
value either inside or outside the neuron, though two data values
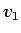 and
and 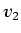 have been tagged and indicated on the
have been tagged and indicated on the 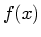 axes
of the
axes
of the 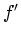 versus
versus  (b) and
(b) and 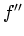 versus
versus  (c) scatterplots.
The neuron boundary seen in the cross-section is irregular because
a range of values occur on either side of the boundary.
Correspondingly, the scatterplots are much more diffuse than
for previous datasets. However, the scattering of hits still
roughly conforms to the over-all shape of the curves we
are looking for.
(c) scatterplots.
The neuron boundary seen in the cross-section is irregular because
a range of values occur on either side of the boundary.
Correspondingly, the scatterplots are much more diffuse than
for previous datasets. However, the scattering of hits still
roughly conforms to the over-all shape of the curves we
are looking for.
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...ramidal-crop-b1.thesis.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img77.gif) |
We finish with Figure 4.8 which shows the
scatterplots for one of the CMDA neuron datasets, generated by
electron microscope (EM) tomography. Unlike the previous datasets,
there is no obvious evidence of clean boundaries in the scatterplots,
only the vague shape of the curves we are looking for. The main for
reason for this is that CT scans provide a better match to our assumed
ideal boundary characteristics than does electron microscope
tomography. It is these EM datasets, where the boundary is less
than ideal, which will be the most severe test of the algorithms
developed in this thesis.
It should be noted that a related technique has been used in computer
vision for feature identification. Panda and Rosenfeld [PR78]
use two dimensional scatterplots of data value and gradient magnitude
to perform image thresholding for night vision applications. They,
however, do not assume a particular boundary model, instead limiting
their analysis of the scatterplot to identifying particular
distributions within regions of low and/or high gradient magnitude.
The techniques which have made possible the display of the various
scatterplots shown so far should be described in greater detail, since
the process for scatterplot visualization has a large effect on how
informative they are. We use the first derivative versus data value
scatterplot for the turbine blade as our example.
Figure 4.9 illustrates how simple approaches to
scatterplot display are not effective. In
Figure 4.9(a), a linear mapping was used to determine
gray level from the number of hits in the scatterplot. The problem is
that the image is too faint because the number of voxels in the
background material (air) overwhelms the number of voxels everywhere
else. This can be alleviated somewhat with a gamma correction
(Figure 4.9(b)), but important detail within the
boundary region curve is not visible.
Figure 4.9:
Methods for scatterplot visualization. In (a), the mapping from number of
voxels accumulated to gray level is linear. The dark spot in the lower
left represents the voxels within background material, air. In (b), a gamma correction
of  was applied to make the image darker, but detail is still lacking.
(c) shows the result of applying histogram equalization to (a), and (d)
shows the result of following histogram equalization with a gamma correction
of
was applied to make the image darker, but detail is still lacking.
(c) shows the result of applying histogram equalization to (a), and (d)
shows the result of following histogram equalization with a gamma correction
of 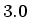 .
.
![\begin{figure}
\setcounter {subfigure}{0}
\psfrag{v}[bl]{\hspace{1.5pt}\ra...
...psfig {figure=eps6/blade/take3.high.eps, width=0.35\textwidth}}
}
\end{figure}](img80.gif) |
To solve this problem we have use a standard contrast enhancement
technique from image processing called histogram
equalization7[GW93]. Histogram equalization flattens the
histogram of the gray levels in an image, so that all gray levels are
utilized approximately equally. Figure 4.9(c) shows
the result of histogram equalization on
Figure 4.9(a). This is an improvement, but since the
image is now too dark, we apply a gamma correction of 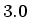 to make
the image lighter. The fine structure with the boundary curve region
of the scatterplot is now visible. The amount of gamma correction
applied after histogram equalization was chosen by hand for each of
the different datasets shown in this thesis.
to make
the image lighter. The fine structure with the boundary curve region
of the scatterplot is now visible. The amount of gamma correction
applied after histogram equalization was chosen by hand for each of
the different datasets shown in this thesis.
Footnotes
- ... blade6
- Dataset courtesy of GE Corporate
Research and Development
- ...
equalization7
- The fact that the image we are processing in
this situation is itself a histogram is not especially meaningful or
important.



Next: Opacity function generation
Up: Histogram volume calculation
Previous: Implementation
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...g {figure=eps/cyl-th3.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img72.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...g {figure=eps/cyl-th3.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img72.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...{figure=eps/shell-th3.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img74.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...g {figure=eps/blade-crop-b1.vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img75.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...ps/engine-crop-b1-rsmp.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img76.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\centering {
\psfrag{v1}[tc]{\h...
...ramidal-crop-b1.thesis.proj-vc.high.eps,
width=0.3\textwidth}}
}
\end{figure}](img77.gif)
![\begin{figure}
\setcounter {subfigure}{0}
\psfrag{v}[bl]{\hspace{1.5pt}\ra...
...psfig {figure=eps6/blade/take3.high.eps, width=0.35\textwidth}}
}
\end{figure}](img80.gif)
![]() to make
the image lighter. The fine structure with the boundary curve region
of the scatterplot is now visible. The amount of gamma correction
applied after histogram equalization was chosen by hand for each of
the different datasets shown in this thesis.
to make
the image lighter. The fine structure with the boundary curve region
of the scatterplot is now visible. The amount of gamma correction
applied after histogram equalization was chosen by hand for each of
the different datasets shown in this thesis.