Homework, material covered

19.10 TERMINOLOGY   When talking about a congruence $a\equiv b\pmod m$, we refer to $a$ as the left-hand side, $b$ the right-hand side, and $m$ the modulus. The plural of "modulus" is moduli.

19.14 DEF (system of simultaneous congruences)  Let $a_1,\dots,a_k,m_1,\dots,m_k\in\zzz$. Consider the following list of congruences. $$\begin{align*} x &\equiv a_1 \pmod{m_1}\\ x &\equiv a_2 \pmod{m_2}\\ &\vdots\\ x &\equiv a_k \pmod{m_k} \end{align*} $$ Such a list is called a "system of simultaneous congruences." The numbers $m_1,\dots,m_k$ are the moduli of the system. Here $x$ is an "unknown," which is just a symbol. We say that a number $x_0\in\zzz$ satisfies this system if $x_0$ satisfies each of congruences on the list, i.e., $(\forall i)(x_0\equiv a_i \pmod{m_i})$. Such a value $x_0$ is called a solution of the system. We also say "$x=x_0$ is a solution." Often we write $x$ for $x_0$, confounding a symbol for an unknown with a number, but the meaning should be clear from the context.
We call the system feasible if it has a solution and infeasible if it has no solution.

19.18 EXAMPLE   Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv 4 & \pmod{15}\\ x &\equiv -5 & \pmod{21}\\ x &\equiv 9 & \pmod{35} \end{align*} $$ This system is feasible because $x=79$ is a solution. (DO verify!)

19.20 DO   Prove: the value $x\in\zzz$ is a solution of the system in the preceding example if and only if $x\equiv 79 \pmod{105}$. In other words, the set of solutions of the system is $105\zzz+79$. What is the relation of the number $105$ to the moduli in this example?

19.22 DEF   Let $H\subseteq \zzz$. Recall the definition of least common multiple of $H$.
We say that the number $k$ is a common multiple of $H$ if $(\forall h\in H)(h\mid k)$
We say that the number $m$ is a least common multiple of $H$ if
(a)   $m$ is a common multiple of $H$
(b)   $(\forall k\in\zzz)($if $k$ is a common multiple of $H$ then $m\mid k)$

19.24 DO   If $m$ is a least common multiple of $H$ then the least common multiples of $H$ are $m$ and $-m$.

19.26 NOTATION   If $m$ is a least common multiple of $H$ then we write $\lcm(H) = |m|$. So the $\lcm$ notation always refers to a non-negative number.

19.28 HW (3+3 points)   (a)   Find   $\lcm(\emptyset)$.  (b)   Find   $\lcm(\zzz)$.

19.30 Bonus (7 points)   THEOREM  Every subset of $\zzz$ has a least common multiple.
Prove this theorem. Give a short and elegant proof, using the theorem that every module is cyclic (Ex. 7.122). Proofs by other methods will not be accepted.

19.32 DO   THEOREM   If the system of simultaneous conguences in DEF 19.14 is feasible then the set of its solutions is a residue class modulo the least common multiple of the moduli.
Beginning of proof. Let $M=\lcm(m_1,\dots,m_k)$. Assume $x=a$ is a solution. Let $S$ denote the set of solutions of the system. We claim that $S = M\zzz+a$. To do so, we need to prove that   (a)   $S\subseteq M\zzz+a$ and   (b)   $S\supseteq M\zzz+a$.

19.34 Bonus (4+3 points)   Complete the proof started in the preceding exercise. Explicitly refer to the items in the definition of the least common multiple.

19.36 EXAMPLE   Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv 4 & \pmod{15}\\ x &\equiv -5 & \pmod{21}\\ x &\equiv 19 & \pmod{35} \end{align*} $$ Claim. This system is infeasible.
PROOF BY CONTRADICTION. Suppose for a contradiction that there is a solution, call it $x_0$. The second congruence implies $x_0\equiv -5 \pmod 7$ (because $7\mid 21$). The third congruence implies $x_0\equiv 19 \pmod 7$ (because $7\mid 35$). By the symmetry and transitivity of congruence mod $7$ we infer that $-5 \equiv 19 \pmod 7$, which means $7\mid 24$, which is false. Our assumption that the system is feasible has led to the false conclusion $7\mid 24$, proving that our assumption was wrong. (In other words, this conclusion contradicts our assumption.) This contradiction proves the Claim. QED

19.38 HW (6 points)   Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv 103 & \pmod{8}\\ x &\equiv -7 & \pmod{55}\\ x &\equiv 13 & \pmod{20} \end{align*} $$ Prove that this system is infeasible.

19.40 CHINESE REMAINDER THEOREM (CRT) Consider the system of simultaneous congruences in DEF 19.14. If the moduli $m_i$ are pairwise relatively prime (i.e., $(\forall i\neq j)(\gcd(m_i,m_j)=1)$) then the system is feasible.

19.42 EXAMPLE. Consider the following system of simultaneous congruences. $$\begin{align*} x &\equiv a & \pmod{8}\\ x &\equiv b & \pmod{55}\\ x &\equiv c & \pmod{63} \end{align*} $$ CRT guarantees that this system is feasible regardless of the values $a,b,c\in\zzz$. (DO verify that the moduli are pairwise relatively prime, i.e., $\gcd(8,55)=\gcd(8,63)=\gcd(55,63)=1$.)

19.44 DO   Prove CRT for $k=2$.
Proof.   We shall find $u_1,u_2\in\zzz$ such that $x=u_1 m_1+u_2 m_2$ is a solution. Observe that the congruence $x\equiv a_1 \pmod{m_1}$ is equivalent to $u_2 m_2 \equiv a_1\pmod{m_1}$, and this congruence is solvable because $\gcd(m_1,m_2)\mid a_1$ (Ex. 10.22). Similarly, the congruence $x\equiv a_2 \pmod{m_2}$ is equivalent to $u_1 m_1 \equiv a_2 \pmod{m_2}$, and this congruence is solvable because $\gcd(m_1,m_2)\mid a_2$.     QED

19.46 DO   Prove CRT by induction on $k$ using the preceding exercise.

19.48 HW (5 points) Find a solution to the following system of simultaneous congruences. Use the method of Ex. 19.44. Other methods, such as guessing, will not be accepted. However, you can use guessing to solve the linear conruences that arise in the course of the solution. Show all your work. $$\begin{align*} x & \equiv -1 & \pmod{23}\\ x & \equiv 10 & \pmod{47}\\ \end{align*} $$

19.50 COMMENT.   CRT gives a sufficient condition of feasibility: the condition that the moduli are pairwise relatively prime suffices for feasibility. It is not a necessary condition of feasibility: a system can be feasible even if the moduli are not pairwise relatively prime. We have seen such a system in Example 19.30. The following exercise expands this observation.

19.52 HW (3 points) Prove: $(\forall m_1,\dots,m_k)(\exists a_1,\dots,a_k)$ such that the system of simultaneous congruences in DEF 19.14 is feasible.   Give a very simple solution.

19.54 DO   Find $m_1,m_2,a_1,a_2\in\zzz$ such that the pair $x\equiv a_i \pmod{m_i}$ $(i=1,2)$ of simultaneous congruences is infeasible and the following conditions are met: $m_1, m_2 >0$,  $m_2 \nmid m_1$,  $m_1 \nmid m_2$ (neither of the two moduli is a divisor of the other), and $m_1+m_2$ is as small as possible subject to these conditions. Prove (in one line) that your system is infeasible. No proof of minimality is required.

19.56 DO   Use CRT to prove that the following system is feasible. Do not compute a solution. $$\begin{align*} x &\equiv 53 & \pmod{363}\\ x &\equiv -2 & \pmod{187}\\ \end{align*} $$ We have $363=3\cdot 11^2$ and $187=11\cdot 17$. So the moduli are not pairwise relatively prime; CRT cannot be applied directly. However, the first congruence is equivalent to the following pair of congruences: $$\begin{align*} (a)\quad & x &\equiv 53 & \pmod{3}\\ (b)\quad & x &\equiv 53 & \pmod{121}\\ \end{align*} $$ and the second congruence is equivalent to this pair of congruences: $$\begin{align*} (c)\quad & x &\equiv -2 & \pmod{11}\\ (d)\quad & x &\equiv -2 & \pmod{17}\\ \end{align*} $$ Now (b) $\Rightarrow$ (c) (why?), so we can omit (c), the system is equivalent to the system (a), (b), (d). This systems has the pairwise relatively prime moduli 3, 121, and 17, therefore it is feasible by CRT.

19.58 HW (6 points)   Use CRT to prove that the following system is feasible. Do not compute a solution. Use the method of the preceding exercise. $$\begin{align*} x &\equiv 379 & \pmod{500}\\ x &\equiv 104 & \pmod{475}\\ \end{align*} $$

19.60 Bonus (9 points) Let $p > q >2$ be primes. Let $n=pq$. Prove: the congruence   $x^2\equiv 1 \pmod{n}$ has a solution $x\not\equiv\pm 1 \pmod n$.

19.70   The RSA public-key cryptosystem

The following result guarantees the success of RSA decoding.
19.75 DO   Let $p,q$ be a pair of distinct primes. Let $N=pq$ and $M=\lcm(p-1,q-1)$. Let $k\ge 1$ and $k\equiv 1\pmod M$. Then   $(\forall x\in\zzz)(x^k\equiv x \pmod N)$.

19.80 DEF (prime counting function)   $\pi(x)$ denotes the number of primes $p\le x$.   Examples: $\pi(10)=4$, $\pi(100)=25$, $\pi(\pi)=2$, $\pi(-1)=0$.

We now state one of the most amazing results of all of mathematics.

19.85 Prime Number Theorem (Jacques Hadamard and Charles de la Vallée Poussin, 1896) $$ \pi(x) \sim \frac {x}{\ln x} $$

19.87 HW (6 points) Pick an $n$-digit integer $x\ge 0$ uniformly at random; initial zeros permitted. (So for $n=4$ we can pick 0037.)
(a)   What is the size of the sample space for this experiment?
(b)   Let $p_n$ denote the probability that $x$ is prime. Prove:   $p_n = \Theta(1/n)$.

19.89 REMARK.   This means picking random integers is a rather efficient method of finding random primes with a given number of digits, as long as we can test the primality of the number we picked. Efficient tests of primality are available; they are based on FlT.

19.100 Bonus (strongly negatively correlated events, 15 points)   Let $A_1,\dots,A_m$ be events such that $(\forall i)(P(A_i)=1/2)$ and $(\forall i\neq j)(P(A_i\cap A_j)\le 1/5)$. Prove:   $m\le 6$.
Hint. Consider the sum of the indicator variables of the events. The solution should be just a few lines.

Class 18, Tue 12-01   All items due Thursday, December 10, 12:30pm.
Proof required except where expressly stated otherwise.

18.10 DO   Prove:   $\ln x = o(x)$ as $x\to\infty$. In other words, $\lim_{x\to\infty} \frac{\ln x}{x} = 0$.
Hint.   L'Hospital's rule.

18.12 HW (5 points)   Prove:   $\ln x = o(\sqrt{x})$ as $x\to\infty$. Do NOT use L'Hospital's rule. Use 18.10 (do not prove) and a change of variables.
This method -- that we use a weaker result to prove a stronger result -- is called bootstrapping.

18.14 DO   Prove: for every $\eps > 0$ we have $\ln x = o(x^{\eps})$. Same instructions as in the preceding exercise: no L'Hospital, just a change of variables.

18.20 DEF   We say that a sequence $a_n$ of real numbers is polynomially bounded if there exists a polynomial $f\in\rrr[x]$ such that for all sufficiently large $n$ we have $|a_n| \le f(n)$.

18.22 DO   Let $a_n$ be a sequence of real numbers. Prove: $a_n$ is polynomially bounded if and only if there exists $c$ such that $a_n=O(n^c)$.

18.24 HW (7 points) Let $a_n\ge 1$ be a sequence of real numbers. Prove: $a_n$ is polynomially bounded if and only if $\ln a_n = O(\ln n)$. You may use the preceding exercises without proof.

18.26 DO   Prove: for every integer $k\ge 0$, the sequence $b_n:=\binom{n}{k}$ is polynomially bounded.

18.28 HW (6 points) Prove: the sequence $g_n:=\binom{n}{\lfloor \ln n\rfloor}$ is not polynomially bounded. You may use all preceding exercises without proof.

18.30 HW (4 points) Find a polynomially bounded sequence of real numbers $u_n\ge 1$ that does not satisfy the relation $u_{n+1} = O(u_n)$.

18.33 NOTATION   $\exp(x) := \eee^x$.
This notation is recommended when $x$ is a tall expression involving subscripts, exponents, fractions, etc.

18.35 DEF   Let $a_n$ be a sequence of positive real numbers. We say that $a_n$ grows exponentially if $$(\exists \eps > 0)(a_n = \exp(\Omega(n^{\eps})))$$

18.36 EXAMPLE   Let $b_n$ be a sequence of positive real numbers. If for all sufficiently large $n$ we have $b_n > \exp(\sqrt{n}/100)$ then $b_n$ grows exponentially.

18.38 DO   Let $a_n$ be a sequence of positive real numbers. Prove:   $a_n$ grows exponentially if and only if the sequence $(\ln \ln a_n)/(\ln n)$ is bounded away from zero, i.e., $\exists \delta > 0$ such that for all sufficiently large $n$ we have $(\ln \ln a_n)/(\ln n)\ge \delta$.

18.40 HW (5 points) Prove: the sequence $F_n$ (Fibonacci numbers) grows exponentially. Your proof should be very simple, just a couple of lines, using nothing but the definition of Fibonacci numbers. Do NOT use any result about the Fibonaci numbers that we did not prove in class.

18.42 DO   Prove: the sequence $n!$ grows exponentially.

18.44 DO   Let $h_n$ be a sequence of positive real numbers such that $h_{n+1} \ge 1.001 h_n$ for all sufficiently large $n$. Prove that $h_n$ grows exponentially.

18.46 Bonus (5 points) Find a sequence $d_n$ of positive real numbers that grows exponentially but satisfies $d_n \sim d_{n+1}$. The description of $d_n$ should be very simple, as should be the proof that $d_n$ satisfies the conditions.

18.50 Bonus (5 points) Let $a_n$ and $b_n$ be sequences of positive real numbers. Suppose $a_n$ is polynomially bounded and $b_n$ grows exponentially. Prove:   $a_n = o(b_n)$. In other words,   $\lim_{n\to\infty} a_n/b_n = 0$   (exponential decay beats polynomial growth). Do NOT use L'Hospital's rule. Use 18.14 (do not prove) and a change of variables.

18.60   Let $G=(V,E)$ be a graph. The greedy algorithm for independent sets proceeds as follows.

    Input: $G=(V,E)$
    Loop invariant: $S\subseteq V$ is an independent set
    Intialize: $S:=\emptyset$
    while there exists a vertex $v\notin S$ such that $S\cup \{v\}$ is independent,
       add such a vertex to $S$
   end(while)
   return $S$

18.62 DO   Prove that the greedy algorithm (a) always returns a maximal independent set   (b) but this independent set is not necessarily maximum.

18.70 Inclusion--Exclusion formula.
Let $A_1,\dots,A_k\subseteq\Omega$ be events and let $B$ denote the complement of their union:   $B=\overline{A_1\cup\dots\cup A_k}$.   Then $$P(B) = S_0 - S_1 + S_2 - + \dots + (-1)^k S_k$$ where $S_t$ denotes the sum of the probabilities of the $t$-wise intersections of the $A_i$. ($S_0=1$.) For instance, for $k=3$ the formula takes the form $$P(B)= S_0 - S_1 + S_2 - S_3 = 1-\left(P(A_1)+P(A_2)+P(A_3)\right)+ \left(P(A_1\cap A_2)+P(A_1\cap A_3)+P(A_2\cap A_3)\right) - P(A_1\cap A_2\cap A_3) $$

18.71 DO   Observe that the number of terms in the definition of $S_t$ is $\binom{n}{t}$.

18.72 DO   Expanding the definition of each $S_t$ we obtain the following equivalent form of the Inclusion--Exclusion formula: $$ P(B) = \sum_{I\subseteq [k]} (-1)^{|I|} P\left(\bigcap_{i\in I} A_i\right) \,.$$

18.73 DO   Let $\vt_A :\Omega\to\{0,1\}$ denote the indicator of event $A$. Recall that $\vt_{\Abar}=1-\vt_A$ and $\vt_{A\cap B} = \vt_A\cdot \vt_B$. Moreover, $E(\vt_A)=P(A)$.

18.74 DO   Deduce the following identity from Ex. 5.76. $$ \prod_{i=1}^k (1-x_i) = \sum_{I\subseteq [k]} (-1)^{|I|} \prod_{i\in I} x_i \,.$$

18.75 PROOF of the Inclusion-Exclusion formula.
Observe that $B=\overline{A_1\cup\dots\cup A_k}=\Abar_1\cap\dots\cap\Abar_k$ and therefore $$\vt_B = \prod_{i=1}^k \vt_{\Abar_i}=\prod_{i=1}^k (1-\vt_{A_i})= \sum_{I\subseteq [k]} (-1)^{|I|} \prod_{i\in I}\vt_{A_i} = \sum_{I\subseteq [k]} (-1)^{|I|} \vt_{\bigcap_{i\in I} A_i} \,.$$ Now applying the expected value operator to each side and using the linearity of expectation, we obtain the equation stated in 18.72.          QED

18.80 HW (6 points) Count those $n$-digit integers which (a) have only odd digits, and (b) have every odd digit among their digits. Examples $(n=7)$: the number 3739513 is counted; the number 3737917 is not counted. Your answer should be a closed-form expression.
Clarification (added 12-9 7pm): This is one question, not two. You have to count those numbers that satisfy both conditions, (a) AND (b).

18.85 DEF   Recall that a permutation of a set $A$ is a bijection $f:A\to A$. A fixed point of $f$ is an element $a\in A$ such that $f(a)=a$. The permutation $f$ is fixed-point-free if it has no fixed points. Fixed-point-free permutations are also called derangements.

18.86 DO (Derangement problem)  Let us pick a random permutation $f:[n]\to [n]$ uniformly. Prove that the probability $p_n$ that $f$ is fixed-point-free is $$ p_n = \sum_{i=1}^n \frac{(-1)^i}{i!} $$ Note that $\lim_{n\to\infty} p_n = 1/\eee$.

18.90   RANDOM GRAPHS: the Erdös--Rényi model.
Let $\graphs(V)$ denote the set of all graphs with vertex set $V$. We write $\graphs(n)$ for $\graphs([n])$. Let $0 < p < 1$. Let $\Gbold(n,p)$ denote the binomial distribution on $\graphs(n)$ defined as follows: for $G\in \graphs(n)$ we set $$P(G)=p^m(1-p)^{\binom{n}{2}-m} .$$

18.92 DO   Let $\calG \sim \Gbold(n,p)$. This means that we choose a graph $\calG\in\graphs(n)$ according to the distribution $\Gbold(n,p)$. For $1\le i, j\le n$, $i\neq j$, let $A(i,j)$ denote the event that $i\sim j$ in $\calG$. (So $A(i,j)=A(j,i)$.) Prove that
   (i)   $P(A(i,j))=p$
   (ii)   the $\binom{n}{2}$ events $A(i,j)$ $(1\le i < j\le n)$ are independent.

In other words, we generate $\calG$ by flipping $\binom{n}{2}$ biased coins with probability $p$ of "heads"; and we make the $i$-th pair of vertices adjacent if the $i$-th coin comes up "heads."

18.94 REMARK   Note that in this model, all parameters of $\calG$ (girth, diameter, chromatic number, independence number, number of cycles of length $k$, etc.) are random variables.

18.96 DO   Determine (a) the expected value and (b) the variance of the number of edges in the random graph $\calG$ in the $\Gbold(n,p)$ model.

18.98 HW (6+3 points)  Let $T_n$ denote the number of triangles in the random graph $\calG$ in the $\Gbold(n,p)$ model. (a) Determine $E(T_n)$.   (b) What is the size of the sample space for this experiment?

18.100 Bonus (20 points)  Let $T_n$ be as in the preceding exercise. (a)   Determine $\var(T_n)$. Give a closed-form expression.   Use FPS 7.8.19; you do not need to prove that result. (b)   Asymptotically evaluate $\var(T_n)$. Show that there exist constants $a,b$ such that $\var(T_n)\sim a n^b$. State the value of $a$ and $b$.

Class 16, Tue 11-19   Items 16.02--16.44 are due Wednesday, November 25, 3:00pm. Items 16.50--16.222 are due Thursday, December 10, 12:30pm.
Proof required except where expressly stated otherwise.

16.02 STUDY the Aces handout. It describes two elegant solutions to problem 13.210 (expected number of Aces in a poker hand) via indicator variables and also discusses a possible mistake regardig the sample space. It is important that you understand this method; it is a model for the solution of other problems where the question is the expected value of a counting variable ("what is the expected number of $\dots$").

16.04 NOTATION   Unless stated otherwise, $G$ will denote a graph with $n$ vertices nd $m$ edges.

16.06 DO   $0\le m\le \binom{n}{2}$. Moreover, $m=\binom{n}{2}$ if and only if the graph is complete ($K_n$).

16.10 DEF   A cycle-free graph is called a forest. A connected cycle-free graph is called a tree.

16.12 DO   Each connected component of a forest is a tree.

16.14 DEF   The girth of a graph is the length of its shortest cycle. The girth of a forest is $\infty$. This follows from our covention that the minimum of the empty set of numbers is $\infty$.

16.16 DO   What is the girth of $K_n$ (the complete graph on $n$ vertices), $C_n$ (the cycle of length $n$), $P_n$ (the path of length $n-1$)?

16.18 HW (6+2 points) [Updated 11-23 15:30: vertices labeled, explanation expanded. Please report if your screen does not display the images properly.]   (a)   Each graph in the images below has 10 vertices, is regular of degree 3, and has girth 5. Are they isomorphic? Prove your answer. If you claim they are not isomorphic, find some invariant that distinguishes them, prove. If you claim they are isomorphic, you need to exhibit an isomorphism, i.e., a bijection $f:\{x_0,\dots,x_9\}\to\{y_0,\dots,y_9\}$ that preserves adjacency. State the bijection, do not prove that it preserves adjaceny.   (b)   The graph on the left is called Petersen's graph. What should we call the other graph? Why?

16.20 Bonus (7 points, due Dec 10)   Let $G$ be a regular graph of degree $k$ (every vertex has degree $k$) and girth $\ge 5$. Prove:   $n\ge k^2+1$.

16.22 HW (1+1+3) For $k=1,2,3$ find a graph $G_k$ that is regular of degree $k$, has girth $\ge 5$, and has $n=k^2+1$ vertices. Name the graphs.

16.24 THEOREM   There exists a regular graph of degree $7$ with $n=50=7^2+1$ vertices and girth $5$. It is called the Hoffman--Singleton graph.

16.26 THEOREM (Alan J. Hoffman and Robert Singleton, 1960)   If there exists a regular graph of degree $k$, girth $\ge 5$, and $n=k^2+1$ vertices then $k\in\{1,2,3,7,57\}$.
The proof of this astonishing theorem is based on the Spectral Theorem of linear algebra, applied to study of the eigenvalues of the adjacency matrix of the graph. The conclusion is reached using Exercise 12.55(a).

16.35 HW (4 points)   Prove: if a tree has $n\ge 2$ vertices then it has a vertex of degree 1.
Hint:   Show that the endpoints of a longest path in the tree must have degree 1 in the tree.
[Update 11-23 8:15pm: condition $n\ge 2$ added.]

16.37 DO   Prove: If $T$ is a tree with $n$ vertices then it has $m=n-1$ edges.   Proceed by induction on $n$. Use the preceding exercise.

16.39 HW (4 points)   Prove: if a forest has $n$ vertices and $c$ connected componets then it has $m=n-c$ edges.

16.42 DO   Draw all non-isomorphic trees with $n \le 6$ vertices. Let $t_n$ denote the number of non-isomorphic trees with $n$ vertices. Show that $t_1=t_2=t_3=1$, $t_4=2$, $t_5=3$, and $t_6=6$.

16.44 HW (18 points; lose 4 points for each mistake)   Draw all non-isomorphic trees with $n=7$ vertices. State, how many you found (the number $t_7$). Avoid the three kinds of mistake: (a) you draw two isomorphic trees (b) you miss a tree (c) you include a graph among your pictures that does not belong (it is not a tree with 7 vertices).
You can draw them by hand and separately upload the sheet of images. Your pictures should be clean and unambiguous. You do not need to prove anything about your pictures. List your graphs in some logical order; indicate in te text how you ordered them.

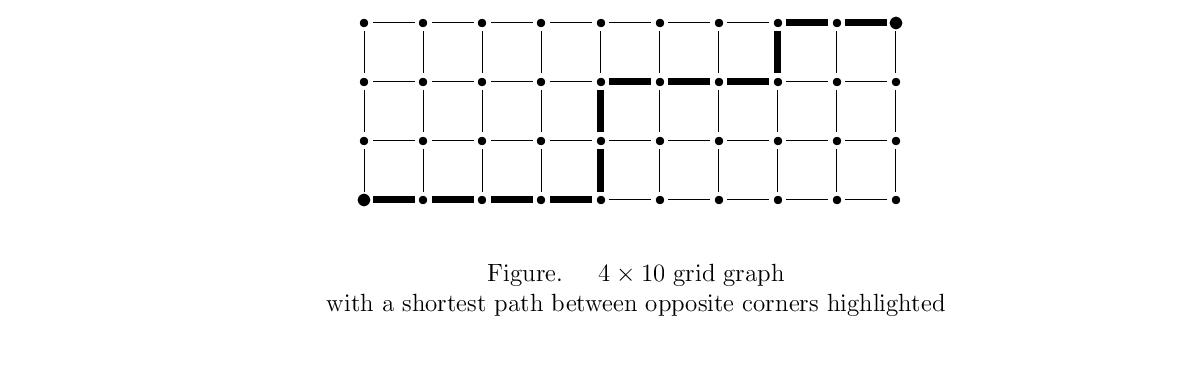
16.50 DEF   Let $k,\ell \ge 1$. The $k\times\ell$ grid graph $\grid(k,\ell)$ has $k\ell$ vertices arranged in a $k\times\ell$ array; the edge set consists of $k$ horizontal paths $P_{\ell}$ and $\ell$ vertices paths $P_k$.
The figure illustrates the $\grid(4,10)$ with a highlighted shortest path between opposite corners.

16.52 HW (2 points, due Dec 10)   Find all counterexamples to the following statement:
    $(\forall k,\ell \ge 1)($the girth of $\grid(k,\ell)$ is $4)$. No proof required, just clearly state the set of pairs $(k,\ell)$ in question, using the set notation.

16.54 DEF   The distance between vertices $x$ and $y$ in a graph $G$ is the length of the shortest paths between $x$ and $y$. If $y$ is not reachable from $x$ (i.e., $x$ and $y$ are not in the same connected component) then $\dist(x,y)=\infty$.
Examples.   (a) $\dist(x,x)=0$ (b) In $K_n$, the distance between any pair of distinct vertices is 1 (c) The distance between the two endpoints of the path $P_n$ is $n-1$.

16.56 DEF   A function $\rho : V\times V \to \rrr$ is a metric if for all $x,y,z\in V$   (a) $\rho(x,y)\ge 0$   (b)   $\rho(x,y)=0 \Leftrightarrow x=y$   (c)   $\rho(x,y)=\rho(y,x)$   (d)   (triangle inequality) $\rho(x,z)\le \rho(x,y)+\rho(y,z)$.

16.58 DO   Let $G=(V,E)$ be a connected graph. Prove that the distance function $\dist(x,y)$ is a metric on $V$.

16.60 DEF   The diameter of a graph $G=(V,E)$ is the quantity $\diam(G) = \max\{\dist(x,y)\mid x,y\in V\}$. In particular, if $G$ is disconnedted then $\diam(G)=\infty$.

16.58 DO   (a)   $\diam(K_n)=1$   (b)   $\diam(P_n)=n-1$ (c)   $\diam(C_n)= \lfloor n/2\rfloor$   (d)   The diameter of the $k\times\ell$ grid is $\diam(\grid(k,\ell))=k+\ell-2$.

16.60 HW (6 points, due Dec 10)   Count the shortest paths from the lower left corner to the upper right corner of a $k\times\ell$ grid. Your answer should be a very simple closed-form expression in terms of $k$ and $\ell$, involving binomial coefficients.

16.65 DEF   A spanning tree of a graph $G=(V,E)$ is a subgraph $T=(V,F)$ (same set of vertices) that is a tree.

16.67 DO   Prove: A graph $G$ has a spanning tree if and only if $G$ is connected.

16.70 HW (4 points, due Dec 10) Let $G$ be a connected graph and $T$ a spanning tree of $G$. Prove:   $\diam(T)\ge \diam(G)$.

16.72 Bonus (15 points, due Dec 10)   Let $G$ be a connected graph of diameter $d$. Prove:  $G$ has a spanning tree of diameter $\le 2d$.

16.75 Cayley's formula   The number of spanning trees of $K_n$ is   $n^{n-2}$.

16.77 DEF   An automorphism of a graph $G$ is a $G\to G$ isomorphism. $\aut(G)$ denotes the set of automorphisms of $G$.

16.79 DO   In this exercise we count automorphisms. Prove:   (a)   if $n\ge 2$ then $|\aut(P_n)|=2$   (b)   if $n\ge 3$ then $|\aut(C_n)|=2n$   (c)   $|\aut(K_n)|=n!$   (d)   if $n\ge 3$ then $|\aut(\star_n)|=(n-1)!$.

16.81 DO   Count the automorphisms of the (a) cube (b) dodecahedron.

16.83 DO   Prove:   $|\aut(\text{Petersen's graph})|=120$

16.85 DO   Count the automorphisms of all trees up to 7 vertices.

16.87 DO   Let $T$ be a tree with $n$ vertices. Prove that among the spanning trees of $K_n$, there are $\frac{n!}{|\aut(T)|}$ that are isomorphic to $T$.

16.90 Bonus (12+5 points, due Dec 10)     (a)   List all non-isomorphic trees with 6 vertices. Count their automorphisms. State, do not prove.   (b)   Use these results and Exercise 16.87 to verify Cayley's formula for $n=6$. Show all your work.

16.92 DO   Use the same strategy to verify Cayley's formula for $n=5$ and $n=7$.

16.100 DO   Let $k,\ell,m\ge 0$ and $k+\ell+m=n$. We define the trinomial coefficient $$ \binom{n}{k,\ell,m} =\frac{n!}{k!\ell!m!} \,.$$

16.102 DO   Prove the Trinomial theorem: $$(x+y+z)^n = \sum_{k,\ell,m:k+\ell+m=n} \binom{n}{k,\ell,m}x^ky^{\ell}z^m$$ where $k,\ell,m$ are nonnegative integers.

16.104 DO   Count the terms in the Trinomial theorem.

16.106 DEF   Let $k_1,\dots,k_s$ be non-negative integers such that $k_1+\dots+k_s=n$. We define the multinomial coefficient $$\binom{n}{k_1,\dots,k_s} = \frac{n!}{\prod_{i=1}^s k_i!}\,$$

16.108 DO   Prove the Multinomial theorem: $$ \left(\sum_{i=1}^s x_i\right)^n = \sum_{k_1,\dots,k_s: \sum k_i=n} \binom{n}{k_1,\dots,k_s} \prod_{i=1}^s x_i^{k_i} \,.$$

16.110 HW (7 points, due Dec 10)   Count the terms in the sum in the Multinomial theorem. In other words, you need to count the solutions of the equation $k_1+\dots+k_s=n$ in nonnegative integers $k_1,\dots,k_s$, where $n$ and $s$ are given. Your answer should be a simple closed-form expression in terms of $n$ and $s$, involving binomial coefficients.

16.112 DO   (a)   Observe that $\binom{n}{k}=\binom{n}{k,n-k}$ where the left-hand side is our familar binomial coefficient and the right-hand side is a multinomial coefficient with $s=2$. (Here $0\le k\le n$.)   (b)   Observe that the Binomial theorem is a special case of the Multinomial theorem.

16.120 DO   (Spanning trees with prescribed degrees)   Let $d_1,\dots,d_n\ge 1$ be integers such that $\sum_{i=1}^n d_i = 2n-2$. Consider the complete graph $K_n$ with vertex set $[n]$.   (a)   Prove that $K_n$ has a spanning tree $T$ such that $(\forall i)(\deg_T(i)=d_i)$.   (b)   Prove that the number of such spanning trees is $$ \frac{(n-2)!}{\prod_{i=1}^n (d_i-1)!} $$ Proceed by induction on $n$.

16.125 Bonus (6 points, due Dec 10) Use the preceding exercise to prove Cayley's formula. Your proof should take just a couple of lines.

16.130 HW (6 points, due Dec 10)   Let $3\le k\le n$. Count the $k$-cycles in $K_n$. Your answer should be a simple closed-form expression in terms of $k$ and $n$, using factorials. Reason your answer.

16.140 DEF   An indepedent set in the graph $G=(V,E)$ is a subset $S\subseteq V$ such that no pair of vertices in $S$ is adjacent. The independence number of $G$, denoted $\alpha(G)$, is the size of the largest independent set in $G$. A maximum independent set in $G$ is an independent set of size $\alpha(G)$. A maximal independent set is an independent set that is not a proper subset of any other independent set.

16.142 DO   Prove:   (a)   $\alpha(P_n)=\lceil n/2\rceil$ (for $n\ge 1$)   (b)   $\alpha(C_n)=\lfloor n/2\rfloor$ (for $n\ge 3$).

16.144 HW (6 points, due Dec 10) Let $G=(V,E)$ be a graph with $n$ vertices and let $\Delta=\max_{x\in V} \deg(x)$ denote its maximum degree. Prove:   $\alpha(G) \ge n/(\Delta+1)$.

16.145 HW (7 points, due Dec 10) Let $\beta(G)$ denote the size of the smallest maximal independent set of $G$. (This is not standard notation.) For every $n$, find the graph with the largest possible ratio $\alpha(G)/\beta(G)$. State the ratio. Prove that it is largest.

16.146 Bonus (8 points, due Dec 10) For $n\ge 3$, determine $\beta(C_n)$.

16.148 Bonus (9 points, due Dec 10) Let $G$ be a non-empty regular graph with $n$ vertices. ("Non-empty" means the graph has at least one edge.) Prove:   $\alpha(G) \le n/2$.

16.150 HW (9 points, due Dec 10)   Prove: $\alpha(\grid(k,\ell))=\lceil k\ell/2 \rceil$. Give a one-line proof that there exists an independent set of this size; and give an elegant proof in a couple of lines that no larger independent set exists. Elegance counts.

16.152 DO   If $A\subseteq V$ is an independent set in the graph $G=(V,E)$ and $B\subseteq A$ then $B$ is an independent set. (Note that the empty set is independent.)

16.154 HW (10 points, due Dec 10) Let $h(n)$ denote the number of independent sets in the graph $P_n$ (the path with $n$ vertices). So $h(1)=2$, $h(2)=3$ (verify!). Express $h(n)$ as a simple closed-form expression that refers to a much-studied sequence.
Hint.  Work out the values of $h(n)$ for small values of $n$ (say, $n\le 4$), observe the pattern, prove the same pattern continues indefinitely.

16.160 DEF   A coloring of the vertices of a graph $G$ is a function $f: V(G)\to C$ where $C$ is a set to which we refer as the set of "colors." A legal coloring is a coloring of the vertices such that adjacent vertices get different colors. In other words, the coloring $f$ is legal if $(\forall x,y\in V(G))(x\sim y \implies f(x)\neq f(y))$. The graph is $k$-colorable if a set $C$ of size $k$ suffices for a legal coloring. The chromatic number $\chi(G)$ is the smallest $k$ such that $G$ is $k$-colorable. ($\chi$ is the Greek letter chi, pronounced "khi".)

16.162 DO   $G$ is $k$-colorable if and only if $k\ge \chi(G)$.

16.164 DO   The chromatic number of $G$ is the smallest value $k$ such that $V(G)$ has a partition into $k$ independent sets.

16.166 DO   $1\le \chi(G)\le n$.

16.168 DO   $\chi(K_n)=n$ and $\chi(\overline{K_n})=1$.

16.170 DO   If $\chi(G)=n$ then $G$ is the complete graph. If $\chi(G)=1$ then $G$ is the empty graph ($\overline{K_n}$).

16.172 DO   $\chi(P_n)=2$ if $n\ge 2$.  $\chi(P_1)=1$.

16.174 DO   Let $n\ge 3$. Prove:  $\chi(C_n)=2$ if $n$ is even and $\chi(C_n)=3$ if $n$ is odd.

16.176 DO   Let $\Delta(G)=\max_{v\in V(G)}\deg(v)$ denote the maximum degree of the graph $G$. Prove:   $\chi(G) \le 1+\Delta(G)$.

16.178 HW (5 points, due Dec 10) The chromatic number is often much smaller than the upper bound $1+\Delta(G)$ in the preceding exercise. For every even value of $n\ge 2$ find a graph $G$ with $n$ vertices such that $G$ is regular of degree $n/2$, yet $\chi(G)=2$.

16.185 STUDY the Greedy coloring online handout.

16.187 DEF   A graph $G$ is bipartite if it is 2-colorable, i.e., $\chi(G)\le 2$.

16.189 DO   Prove:   The grid graphs are bipartite.

16.191 DO   Prove: every tree is bipartite.

16.193 DO   Prove: $C_n$ is bipartite if and only if $n$ is even.

16.195 THEOREM   $G$ is bipartite if and only if $G$ does not contain an odd cycle.

16.197 DO   Prove this theorem. The necessity of obvious; we need to prove the sufficiency.
Assumption: $G$ has no odd cycles.
Desired conclusion: $G$ is bipartite.
Outline of the proof. (DO: fill in the details.) First prove that it suffices to prove the theorem for conected graphs. Next, pick a spanning tree $T$ in $G$ and color it by 2 colors. Prove: if this is not a legal coloring of $G$ then $G$ has an odd cycle $C$ such that all but one of the edges of $C$ belong to $T$.

16.200 Bonus (15 points, due Dec 10)   Let $G$ be a graph with $m$ edges. Prove: $G$ has a bipartite subgraph with $\ge m/2$ edges.

16.202 HW (7 points, due Dec 10)   $\alpha(G)\cdot \chi(G) \ge n$.

16.204 HW (5 points, due Dec 10) Show that for every $n\ge 2$ there is a graph $G$ such that $\alpha(G)\cdot \chi(G) \ge n^2/4.$

16.206 Bonus (14 points, due Dec 10) Prove: If $G$ is triangle-free then $\chi(G) \le 1+2\sqrt{n}$.

16.210 STORY   "Merlin Colorings" (MC) is a firm that specializes in optimally coloring graphs "while you wait." A client brings MC a large graph $G$. Merlin, the owner, has the supernatural ability to tell the chromatic number of any graph just by quickly glancing at it. He tells the client that her graph has chromatic number 4.
The client does not trust him, she wants proof. Merlin quickly produces a 4-coloring (coloring that uses only 4 colors). The client checks it on her laptop. This gives her the upper bound $\chi(G)\le 4$. But she is not satisfied.
"Can you tell me why this coloring is optimal?" What she is asking is for Merlin to give her a proof that her graph is not 3-colorable. In other words, she wants a matching lower bound: $\chi(G)\ge 4$.
That demand may spell trouble for Merlin. He tells her that he is willing to give a proof if she is patient enough. The proof will be exponentially long. For all we know, Merlin may be right; a shorter proof may not exist.
As patient as the client may be, that much time she does not have; for reasonable-size graphs (say, a few thousand vertices) this would require her to listen to the proof until the universe cools down to a fraction of a Kelvin, there are no stars anymore and no planets, and the black holes begin emitting particles.
Proving lower bounds on the chromatic number is, in general, a tough job. There are graph of high chromatic number for no obvious reason. The deal is off.

16.215 DO   An easy lower bound: if $G$ contains a clique of size $k$ (complete subgraph with $k$ vertices) then $\chi(G)\ge k$.

That was easy. Now what if the graph does not have large cliques.

16.218 HW (5 points, due Dec 10) Construct a graph $G$ with 6 vertices such that $G$ does not contain a 4-clique ($K_4$ subgraph) and is not 3-colorable ($\chi(G)\ge 4$). The graph should be very simple to describe. Draw it so that it has a symmetry of order 5: if you rotate the plane by 72 degrees, the picture should not change. (Examples: our first drawing of Petersen's graph exhibits a symmetry of order 5; the second picture, a symmetry of order 3. The regular pentagon has a symmetry of order 5.)
Do not prove that your graph has no 4-clique, but do prove that it is not 3-colorable.

16.220 HW (12 points, due Dec 10) Construct a triangle-free graph $G$ with 11 vertices such that $G$ is not 3-colorable. Draw it so that it has a symmetry of order 5.
Do not prove that your graph is triangle-free, but do prove that it is not 3-colorable.

16.222 THEOREM   For every $k$ there exists a triangle-free graph of chromatic number $\ge k$.

16.230 DEF   Let $G$ be a graph with $n$ vertices. A Hamilton cycle in $G$ is a subgraph of $G$ that is a cycle of length $n$, i.e., a cycle that passes through every vertex.

16.232 DO   The dodecahedron graph has a Hamilton cycle.

16.234 DO   The Petersen graph has no Hamilton cycle.

16.236 DO   If $k,\ell\ge 2$ and $k\ell$ is even then $\grid(k,\ell)$ has a Hamilton cycle.

16.238 HW (8 points) If $k\ell$ is odd then $\grid(k,\ell)$ does not have a Hamilton cycle. Give an elegant, short proof. Elegance counts.

Class 15, Tue 11-17   Problems due Wednesday, November 25, 3:00pm, except where stated otherwise. Proof required except where expressly stated otherwise.

15.10 DO   Let $(\Omega,P)$ be a finite probability space. Let $S=\{a\in\Omega\mid P(a)=0\}$. Prove:   (a)   $(\forall A\subseteq\Omega)(P(A)=0 \Leftrightarrow A\subseteq S)$   (b)   If $|S|=k$ then the number of events of probability $0$ is $2^k$ and the number of trivial events is $2^{k+1}$.

15.12 REVIEW Sections 7.1-7.4 and 7.7-7.10 of the instructor's online notes "Finite Probability Spaces (FPS)" and the related items 13.14--13.16 and 13.90--13.218 below.

15.14 DO   Let $X \ge 0$ be a nonnegative random variable with expected value $E(X)=1$. Prove:   $P(X\ge 100) \le 0.01$.
Hint. This is a special case of Markov's Inequality (FPS 7.7.14).

15.16 HW (5 points, due Dec 10) Construct a probability space and a nonnegative random variable $X$ such that $E(X)=1$ and $P(X \ge 0.01) = 10^{-6}$. Make your sample space as small as possible. Make sure you give a clear definition of your sample space, the probability distribution, and the random variable $X$.

15.20 HW (4 points, due Dec 10) Let $X_1,\dots,X_n$ be pairwise independent random variables on the same probability space. Prove: $$ \var\left(\sum_{i=1}^n X_i\right) = \sum_{i=1}^n \var(X_i)\,.$$ Use the following two exercises from FSP without proof: FSP 7.8.19 and FSP 7.9.3. Explain, how the equation above follows from those two exercises. Solutions that do not follow these instructions will not be accepted.

15.22 Bonus (12 points)   FPS 7.9.4 (uncorrelatedness of random variables does not imply their independence).

15.24 DO   FPS 7.10.2--7.10.5 (independence of random variables)

15.26 HW (4+6+6+8, due Dec 10) Let us roll $n$ dice. Let $X_i$ denote the number shown on the $i$-th die (so $1\le X_i\le 6$). Let $Y=\sum_{i=1}^n X_i$ and $Z=\prod_{i=1}^n X_i$. Calculate   (a)   $E(Y)$   (b)   $\var(Y)$   (c)   $E(Z)$   (d)   $\var(Z)$. Each of your answers should be a simple closed-form expression. Reason your answers.

15.30 HW (8 points, due Dec 10) With the notation of the preceding exercise, let $q_n=P(Z \ge 4^n)$. Prove that $q_n$ is exponentially small, i.e., there exists a constant $c > 1$ such that for all sufficiently large $n$ we have $q_n < c^{-n}$. Use Markov's Inequality (FPS 7.7.14).

15.32 Bonus (25 points, due Tuesday, Dec 10) With the notation of the preceding exercise, let $r_n=P(Z \ge E(Z))$. Prove that $r_n$ is exponentially small. Note that a direct application of Markov's Inequality only gives the trivial bound $r_n \le 1$, so it is useless. Instead, apply Markov's Inequality to the variables $W_i = \sqrt{X_i}$. Avoid all numerical calculation you might need to find the expected value of the $W_i$; instead, use the inequality between the arithmetic and the quadratic mean.

15.40 STUDY LN (instructor's online Discrete Mathematics lecture notes), Section 6.1 "Graph Theory terminology."

15.42 HW (6 points)   Find two nonisomorphic regular graphs of the same degree on six vertices. Minimize the number of edges. Give very simple descriptions of your graphs in terms of graphs for which we already have names, like paths, cycles, complete graphs, complement of a graph, etc.). Do not prove that your graphs have minimum possible number of edges (but do prove that they are not isomorphic).

15.44 HW (2+5 points)   Recall that a graph $G$ is self-complementary if it is is isomorphic to its complement: $G\cong \Gbar$. (a) Find a self-complementary graph on $4$ vertices and a self-complementary graph on $5$ vertices. In each case, your graph should be a graph for which we have a name and standard notation; state the name and the notation. Do not prove.   (b)   Prove: if $G$ is self-complementary then $n\equiv 0$ or $1 \pmod 4$.

15.46 DEF   Let $G=(V,E)$ be a graph. A walk of length length $k$ from vertex $s$ to $t$ (source to terminus, start to target) is a list $x_0,\dots,x_k$ of vertices such that $s=x_0$, $y=x_k$, and for each $i$ (1\le i\le k)$, $x_{i-1}\sim x_i$ (where $\sim$ indicates adjacency).

15.48 DO   A walk of length zero exists from $s$ to $t$ if and only if $s=t$.

15.50 DEF   A path of length $k$ in $G$ is a subgraph isomorphic to $P_k$. A path of length $k$ between vertices $s$ and $t$ can be represented as a walk of length $k$ from $s$ to $t$ without repeated vertices, with the caveat that a walk is directed whereas a path is not, so the path $(x_0,\dots,x_k)$ is the same as the path $(x_k,\dots,x_0)$.

15.52 DO   A path of length zero exists from $s$ to $t$ if and only if $s=t$.

15.54 HW (5 points) Let $G=(V,E)$ be a graph and $s,t\in V$. Prove: if there exists a walk from $s$ to $t$ then there is a path between $s$ and $t$.
Hint. Show that the shortest walk from $s$ to $t$ has no repeated vertices.

15.56 DEF   Let $G=(V,E)$ be a graph and let $x,y\in V$. We say that $y$ is reachable from $x$ if there exists a path between $x$ and $y$.

15.58 DO   Prove that the reachability relation is an equivalence relation on $V$. To prove transitivity, use 15.54.

15.60 DEF   The equivalence classes of the reachability relation are the connected components of the graph. So two vertices are in the same connected component if there is a path between them. A graph is connected if it has only one connected component. In other words a graph is connected if tere is a path between each pair of vertices. A graph that is not connected is disconnected.

15.63 Bonus (5 points) Prove: if $G$ is disconnected then its complement $\Gbar$ is connected.

15.70 HW (4 points) Name the smallest graph $G$ such that $G$ is triangle-free (has no $K_3$ subgraph) and $\chi(G)\ge 3$ (requires at least 3 colors, i.e., it is not 2-colorable). "Smallest" means it has the fewest vertices and among those with the fewest vertices, it has the fewest edges. Do not prove that your graph has the required properties. Just name your graph with a word (its standard name) and notation (which we used in class).

More to follow, please check back later.

Class 14, Thu 11-12   Problems due Wednesday, November 25, 3:00pm, except where stated otherwise. Proof required except where expressly stated otherwise.

14.10 DEF   The arithmetic mean or (simple) average of the real numbers $a_1,\dots,a_n$ is the quantity $$ A(a_1,\dots,a_n) = \frac{a_1+\dots+a_n}{n}\,.$$

14.12 DEF   Let $(p_1,\dots,p_n)$ be a probability distribution, i.e., $p_i\ge 0$ and $\sum_{i=1}^n p_i = 1$. The weighted average of $a_1,\dots,a_n$ with weights $p_i$ is the quantity $$ \sum_{i=1}^n p_ia_i.$$

If $p_1=\dots=p_n=1/n$ (uniform distribution), we get the arithmetic mean.

14.14 DO   If $m$ is a weighted average of $a_1,\dots,a_n$ then $\min_i a_i \le m \le \max_i a_i$.

14.16 DEF   The quadratic mean of $a_1,\dots,a_n$ is the quantity $$ Q(a_1,\dots,a_n) = \sqrt{A(a_1^2,\dots,a_n^2)} = \sqrt{\frac{a_1^2+\dots+a_n^2}{n}} $$

14.18 DO   Prove:   $(\forall a_1,\dots, a_n\in\rrr)(A(a_1,\dots,a_n)\le Q(a_1,\dots,a_n))$. Show that equality holds $(Q=A)$ if and only if $a_1=\dots =a_n\ge 0$.
(a)   Deduce this from the Cauchy--Schwarz inequality.   (b)   Deduce this directly from the definition.

14.20   Let $a_1,\dots,a_n > 0$.   The geometric mean of $a_1,\dots,a_n$ is the quantity $$ G(a_1,\dots,a_n) = \left(\prod_{i=1}^n a_i\right)^{1/n}\,$$

14.22 THEOREM   Let $a_1,\dots,a_n > 0$. Then $$G(a_1,\dots,a_n) \le A(a_1,\dots,a_n)\,.$$ Equality holds $(G=A)$ if and only if $a_1=\dots =a_n$.

14.24 DO   Prove Theorem 14.22 for $n=2$.

14.26 DO   Prove Theorem 14.22 for $n=4$.
Hint.   Observe that $A(a_1,a_2,a_3,a_4)=A(A(a_1,a_2), A(a_3,a_4))$ and the analogous identity holds for the geometric mean. Use the preceding exercise.

14.28 DO   Prove Theorem 14.22 for $n=3$ using the preceding exercise.

14.30 Bonus (7 points)   Prove Theorem 14.22 for $n=2^k$. Use the method of 14.26. Proofs by other methods will not be accepted.

14.32 Bonus (7 points)   Prove Theorem 14.22 for all $n$, given that we have already proved it for powers of 2. Use the method of 14.28. Proofs by other methods will not be accepted.

14.34 DEF   Let $a_1,\dots,a_n > 0$. The harmonic mean of of $a_1,\dots,a_n$ is the quantity $$ H(a_1,\dots,a_n) = \frac{1}{A\left(\frac{1}{a_1},\dots,\frac{1}{a_n}\right)} = \frac{n}{\frac{1}{a_1}+\dots +\frac{1}{a_n}}\,.$$

14.36 HW (6 points)   Let $a_1,\dots,a_n > 0$. Prove: $$H(a_1,\dots,a_n) \le G(a_1,\dots,a_n)\,.$$ Equality holds $(H=G)$ if and only if $a_1=\dots =a_n$.
Use Theorem 14.22.

14.38 DO   The road from point $A$ to point $B$ consists of $n$ segments of equal length. A car travels from $A$ to $B$. It passes through the $i$-th segment at speed $v_i$. Prove, that the average speed of the car from $A$ to $B$ is $H(v_1,\dots,v_n)$.

14.40 DO   Let $a_1,\dots,a_n > 0$. Prove the two extreme inequalities in this series: $$\min_i a_i \le H(a_1,\dots,a_n)\le G(a_1,\dots,a_n)\le A(a_1,\dots,a_n)\le Q(a_1,\dots,a_n)\le \max_i a_i\,.$$

14.45 HW (6 points)   (a)   Prove that for all $n\ge 2$ we have   $\displaystyle n! < \left(\frac{n+1}{2}\right)^n$. Use the inequality between the arithmetic and the geometric mean.   (b)   Prove that $n! = o\left((n/2)^n\right)$ (little-oh notation). Use Stirling's formula.

Class 13, Tue 11-10   Problems due Monday, November 16, 11:59pm, except where stated otherwise. Proof required except where expressly stated otherwise.

13.10 ONLINE NOTES:

• LN:   instructor's online lecture notes
• FSP:   Finite Probability Spaces

13.12 STUDY LN, Sections 2.3 and 2.4: "Asymptotic notation," little-oh, big-Oh, $\Omega$ (\Omega), $\Theta$ (\Theta) notation.

13.13 LaTeX for $a_n\sim b_n$ is   $\texttt{\$a_n \sim b_n\$}$

13.14 STUDY the following sections of FPS:

• Sections 7.1 "Finite probability spaces, events,"
• Section 7.2 "Conditional probability, probability of causes,"
• Section 7.3 "Independence, positive and negative correlation of a pair of events,"
• Section 7.4 "Independence of multiple events,"
• Section 7.7 "Random variables, expected value, indicator variables, Bernoulli trials"
• Section 7.8 "Variance, covariance, Chebyshev's Inequality"
• Section 7.9 "Independence of a pair of random variables"
• Section 7.10 "Independence of random variables"

13.15 STUDY the standard deck of 52 cards. The $52=4\times 13$ cards come in 4 suits (spades, hearts, diamonds, clubs) and 13 kinds ($2,3,\dots,10$, Jack, Queen, King, Ace). So, for instance, the deck contains four "nines": the nine of spades, the nine of hearts, the nine of diamonds, and the nine of clubs. A poker hand is a set of five cards, so there are $\binom{52}{5}$ poker hands. Study the various types of pokers hands of interest (pair, two pair, three of a kind, straight, flush, full house, four of a kind, straight flush, royal flush). This is one of the many websites that explain them. These types are ranked by their frequency, the least frequent having the highest value.

13.16 DO   For each of the types listed, calculate the probability that a random poker hand (set of 5 cards) is of the given type. E.g., what is the probability that you are dealt a full house, or a flush.

13.18 REVIEW the handout "Euclid's algorithm and multiplicative inverse"   (click "Texts" on the banner).

13.19 DEF   Let $\Omega$ be a set and $A\subseteq\Omega$. The characteristic function of $A$ relative to $\Omega$ is the function $f_A :\Omega\to \{0,1\}$ defined by $$ f_A(x) = \begin{cases} 1 &\text{ if }& x\in A \\ 0 &\text{ if }& x \in \Abar \end{cases} $$ where $\Abar=\Omega\setminus A$ is the complement of $A$in $\Omega$.

13.20 DO   Prove: Given a function $g:\Omega\to\{0,1\}$ there exists a unique set $A\subseteq\Omega$ such that $g=f_A$.
This means that the correspondence $A\mapsto f_A$ establishes a bijection between the powerset of $\Omega$ and the set of functions $\Omega\to\{0,1\}$.

13.21 DO   Let $A,B\subseteq\Omega$. Prove:   (a)   $f_{A\cap B} = f_A\cdot f_B$   (b)   $f_{\Abar} = 1 - f_A$.

13.22 Bonus (6 points, due Nov 25) Evaluate the sum $$\sum_{A\subseteq B\subseteq [n]} 1 \,.$$ So the summation is over all pairs $(A,B)$ such that $A\subseteq B\subseteq [n]$. Your answer should be a very simple closed-form expression, with a simple proof.

13.23 CONVENTION   In this section, the term "sequence" refers to an infinite sequence of real numbers, unless specified otherwise.

13.24 DO   If $a_n\sim b_n$ and $x_n\sim y_n$ then $a_n x_n \sim b_n y_n$ and $a_n/x_n \sim b_n/y_n$.

13.25 HW (3+4 points) (a) Prove: $\lim_{n\to\infty} (\sqrt{n+1}-\sqrt{n}) = 0$.   (b) Prove: there exist real numbers $a,b$ such that $\sqrt{n+1}-\sqrt{n} \sim an^b$.   Find $a,b$.

13.26 DO   Let $a,b,x,y > 0$. Assume $a/x \le b/y$. Prove:   $a/x \le (a+x)/(b+y) \le b/y$.

13.27 Bonus (5 points) Prove: If $a_n, b_n, x_n, y_n > 0$ and $a_n\sim b_n$ and $x_n\sim y_n$ then $a_n+x_n \sim b_n+y_n$. You may use other exercises from this section without proof; indicate what you are using.

13.28 DO   If $a_n, b_n > 0$ and $a_n\sim b_n$ then $\sqrt{a_n} \sim \sqrt{b_n}$.

13.30 HW (4 points) Find sequences $a_n, b_n$ such that $a_n, b_n \to \infty$ and $a_n\sim b_n$ but $2^{a_n} = o(2^{b_n})$ ("little-oh notation").

13.32 HW (4 points) Prove: there exist real numbers $a,b$ such that $\binom{n}{5} \sim a n^b$. Find $a,b$. You may use 13.24 without proof. Elegance counts.

13.34 DEF   We say that $a_n = \Theta(b_n)$ if there exist $c, C > 0$ such that for all sufficiently large $n$ we have $c|a_n|\le |b_n|\le C|a_n|$.

13.36 DO   Let $f$ be a polynomial of degree $k$ with leading term $a_kx^k$. Prove:   $f(n) = \Theta(n^k)$.

13.38 HW (7 points, due Nov 25)   Let $a_n, b_n > 0$ and $a_n \to\infty$. Prove: If $a_n=\Theta(b_n)$ then $\ln a_n \sim \ln b_n$.

13.40 HW (4+3 points) Let $a_n, b_n > 0$.   (a) Prove: if $\lim_{n\to \infty} a_n/b_n=L$ exists and $0 < L < \infty$ then $a_n = \Theta(b_n)$.
(b)   Prove that the converse is false: find two sequences, $a_n$ and $b_n$, of positive numbers such that $a_n=\Theta(b_n)$ but $\lim_{n\to \infty} a_n/b_n$ does not exist.

13.50 HW (5 points) Let $1\le k \le n/2$. Prove: $$ \binom{n}{k-1} < \binom{n}{k} $$

13.52 HW (5 points) Let $n\ge 0$. Prove: $$ \binom{2n}{n} \le 4^n $$ Hint. Look at the sum of row number $2n$ in Pascal's triangle. Use the preceding exercise.

13.54 HW (5 points, due Nov 25) Let $n\ge 0$. Prove: $$ \binom{2n}{n} \ge \frac{4^n}{2n+1} $$ Hint. Two preceding exercises.

13.58 RECALL Stirling's formula: $$ n! \sim \left(\frac{n}{\eee}\right)^n\cdot\sqrt{2\pi n} $$

13.60 HW (5 points) Asymptotically evaluate the binomial coefficient $\binom{2n}{n}$. Prove that there exist constants $a,b,c$ such that $\binom{2n}{n} \sim a\cdot n^b \cdot c^n$. State the values $a,b,c$. Use Stirling's formula.
[Nov 15, 0:03 update: deleted the word "postive" that erroneously appeared in the previous version of this problem.]

13.62 HW (4 points) Let $a_n, b_n$ be sequences of positive numbers. Prove: if $a_n = o(b_n)$ ("little-oh notation") then for all sufficiently large $n$ we have $a_n < b_n$.

13.68 RECALL:   For all $x\in\rrr$ we have       $\displaystyle{\eee^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}}$ .

13.70 Bonus (4+2)   (a)   Prove:   $(\forall n\ge 0)(n!\ge (n/\eee)^n)$.   Use the power series expansion of $\eee^x$ (13.68).
(b)   Reason why (a) does not follow from Stirling's formula as stated above.

13.72 HW (4+1 points)   (a)   Use Stirling's formula to prove that   $(n/\eee)^n = o(n!)$   ("little-oh notation") (b)   Infer from (a) that the inequality $n! \ge (n/\eee)^n$ holds for all sufficiently large $n$.  Do not use the preceding exercise; use 13.62.

13.74 HW (5 points, due Nov 25)   Use the 13.70 to prove that if $1\le k\le n$ then     $\displaystyle{\binom{n}{k} \le\left(\frac{\eee n}{k}\right)^k}$ . Solving 13.75 does not earn you credit for this problem; give a very simple proof.

13.75 Bonus (7 points, due Nov 25)   Prove: if $1\le k\le n$ then $$\sum_{i=0}^k \binom{n}{i} \le \left(\frac{\eee n}{k}\right)^k\,.$$

13.76 Bonus (6 points) Let $B(n)$ denote the $n$-th Bell number (DEF 8.56). Prove:   $\ln B(n) \sim n\ln n$.
Proceed as follows.   (1)   Prove: $(\forall n)(\ln B(n) \le n\ln n)$.   (2)   Prove: $(\forall \eps >0)(\exists n_0)(\forall n > n_0) (\ln B(n) > (1-\eps)n\ln n)$.   Use 8.64.   (3)   Show that (1) $\wedge$ (2) $\Rightarrow$ $\ln B(n) \sim n\ln n$.

13.80 HW (5+5 points) Prove:   $\ln (n!) \sim n\ln n$.   (a)   Use Stirling's formula and 12.116.   (b)   Do not use Stirling's formula. Instead, use the preceding exercise and 8.62.

13.90 DO   Exercises FPS 7.1.2-7.1.7.

13.92 DO   Exercises FPS 7.1.8 (modular equation), 7.1.10 (union bound),

13.94 DO   Exercise FPS 7.2.2 (iterated conditional probability)

13.96 HW (3+3 points) FPS 7.1.5 (d3) (d4) (coin flips - fair coin)

13.98 HW (6 points, due Nov 25) FPS 7.1.6 (b1) (biased coin)   You need to base your proof on formula FPS (7.3) and not on an intuitive understanding of the meaning of the variable $X_i\,$.
In another terminology, you are asked to compute the marginal distribution (the distribution of the variable $X_i$), given the joint distribution of the variables $(X_1,\dots,X_n)$, i.e., the probability distribution on $\Omega_n$.

13.100 HW (5 points) FPS 7.1.6 (c3) (biased coin, $k$ heads).   Same caveat as in the preceding exercise.

13.102 Bonus (7 points, due Nov 25) FPS 7.1.6 (c4) (biased coin, even number of heads).   Same caveat as in the preceding exercise.

13.104 HW (1+2+3+2 points) FPS 7.2.3 (3 dice)

13.108 DO   FPS 7.2.4 (Theorem of Complete Probability)

13.110 HW (2+8+2 points, due Nov 25) FPS 7.2.5 (Probability of causes)

13.115 DO   FPS 7.3.2 (independence vs. conditional probability)

13.120 HW (4 points) FPS 7.3.4 (independence of complement)

13.122 DO   FPS 7.3.5 (independence of trivial event)

13.123 HW (3 points)   Let $A$ be an event. Prove: $A$ and $A$ are independent if and only if $A$ is a trivial event.

13.124 HW (2 points)   FPS 7.3.6 (indepence with a die)

13.126 HW (6 points, due Nov 25)   FPS 7.3.7 (independence in a prime-size uniform space)

13.128 DO   FPS 7.3.8 (lower bound on the size of the sample space for a pair of nontrivial independent events)

13.135 DO   FPS 7.3.10   (positive/negative correlation reflected in conditional probability)

13.136 Bonus (8 points)   Prove: if events $A$ and $B$ are positively correlated then their complements, $\Abar$ and $\Bbar$, are also positively correlated. The proof should be short. Elegance counts.

13.140 Bonus (9 points, due Nov 25) FPS 7.3.11 (correlation of divisibility by 2 and 3). For 6 points partial credit, solve the problem for $n=25, 26$ and $29$.

13.142 DO   FPS 7.3.12 (inclusion vs. independence)

13.143 HW (4 points)   Let $A,B$ be nontrivial events. Assume $A\subseteq B$. Prove: $A$ and $B$ are positively correlated.

13.144 HW (5 points, due Nov 25) FPS 7.3.13 (when are union and intersection independent?)

13.146 DO   FPS 7.4.3 (independence of complement among 3 events)

13.148 DO   FPS 7.4.4 (independence of trivial event among 3 events)

13.161 HW (5 points, due Nov 25)   Let $A,B,C$ be independent events. Prove: $A\cup B$ and $C$ are independent.

13.162 DO   Let $A,B,C$ be independent events. Prove: $A\cap B$ and $C$ are independent.

13.163 Bonus (5 points, due Nov 25) FPS 7.4.6 (lower bound on the size of the sample space for 3 independent nontrivial events)

13.165 HW (3+9 points, due Nov 25) FPS 7.4.7 (3 pairwise but not fully independent events). For (b), you have to give a clear definition of your probability space (sample space, probability distribution) and the three events in question, prove their pairwise independence, and prove that they are not fully independent.

13.167 HW (4 points, due Nov 25) FPS 7.4.8 (a) (intersection of 3 events)

13.169 Bonus (5 points, due Nov 25) FPS 7.4.8 (b) (intersection of 3 events of prob $1/2$). Note: solving this problem will not earn you credit toward the preceding problem.

13.172 DO  (definition of independence of $k$ events) Prove that Definitions FPS 7.4.10 and FPS 7.4.11 are equivalent.

13.174 DO   (a) FPS 7.4.16 (b) FPS 7.4.17 (independent events can be switched to complement)

13.176 DO   FPS 7.4.18 (if $\exists$ $k$ nontrivial independent events then $|\Omega|\ge 2^k$ .

13.180 DEF   Expected value (FPS 7.7.2)   Let $X:\Omega\to \rrr$ be a random variable. Recall that its expected value is $\sum_{a\in\Omega} X(a)P(a).$

13.182 HW (3+2 points)   Let us consider the probability space $(\Omega,P)$ and the random variable $X:\Omega\to\rrr$ where $\Omega = \{r,s,t\}$ and the probability distribution $P$ and the random variable $X$ are defined by the table $$\begin{array}{|c||c|c|c|} \hline a & r & s & t\\ \hline P(a) & 1/2 & 1/6 & 1/3\\ \hline X(a) & 4 & -12 & -9\\ \hline \end{array} $$ Determine   (a)   $E(X)$ and   (b)   $E(X^2)$. Do not use electronic devices. Show all your work.

13.184 DO   FPS 7.7.5   $\min X \le E(X) \le \max X$

13.185 DO   FPS 7.7.6   $E(\sum X_i) = \sum E(X_i)$

13.186 DO   FPS 7.7.7   (Linearity of expectation)

13.189 DO (FPS 7.7.3) (expressing the expected value in terms of the range)   $E(X) = \sum_{r\in\rrr} r\cdot P(X=r)$.   Note that the event "$X=r$" is the same as $\{a\in\Omega\mid X(a)=r\}$. In yet other words, it is $X^{-1}(r)$.
For the proof, for each $r$, combine all those terms in Def. 13.15 for which $X(a)=r$.   Note that while the number of terms seems infinite, the actual number is the size of the range of $X$. (The rest is zero. Why?)
One advantage of this expression is that the size of the range is usually much smaller than the sample space. For instance, in the case of a sequence of $n$ coin flips, the sample space has size $2^n$, but the number of heads can only take $n+1$ values.

13.191 DEF   An indicator variable is a $(0,1)$-valued random variable $X:\Omega\to\{0,1\}$.

13.192 DO (FPS 7.7.9)   There is a bijection between events and indicator variables. The indicator of event $A\subseteq\Omega$ is the variable $\vt_A$ defined by $$ \vt_A(x) = \begin{cases} 1 &\text{ if }& x\in A \\ 0 &\text{ if }& x \in \Abar \end{cases} $$ This is is the same concept as the characteristic function (Def. 13.19). Review characteristic functions.

13.193 LaTeX   The letter $\vt$ is the lower-case Greek theta. In LaTeX it is denoted by \vartheta.

13.195 DO (FPS 7.7.11)   $E(\vt_A) = P(A)\,.$   Hint. 13.189.

13.197 WARNING (probability vs. expected value)  Events have probability; they do not have expected value. Random variables have expected value; they do not have probability. 13.195 establishes a connection between these concepts.

13.199 DEF   A "Bernoulli trial" is an experiment with only two outcomes: "success" and "failure." This is the same as flipping a biased coin, where "heads" means "success" and "tails" means "failure."

13.200 DEF   Another name of an indicator variable is a Bernoulli random variable. Indeed, we can view every indicator variable as the indicator of "success" of Bernoulli trial.

13.204 DO   Show that the expected number of successes in a sequence of $n$ Bernoulli trials with probability $p$ of success is $np$.   Use Ex. 13.189. Assume the Bernoulli trials are independent.
Proof. (Explain each step!) Let $X$ denote the number of successes. Then $P(X=k) = \binom{n}{k}p^k(1-p)^{n-k}$, and therefore $$E(X)=\sum_{k=0}^n k\binom{n}{k}p^k(1-p)^{n-k} = np\sum_{k=1}^n\binom{n-1}{k-1}p^{k-1}(1-p)^{n-k}=np(p+(1-p))^n = np\,.$$

Note: This was an unintuitive technical proof. Next, we give an intuitive proof of a much stronger result.

13.206 DO   Let $X$ denote the number of successes in a sequence of $n$ Bernoulli trials, where the $i$-th trial has probability $p_i$ of success. Show that $E(X) = \sum_{k=1}^n p_k$. For this result to hold, the Bernoulli trials do not need to be independent.
Proof. Let $Y_i$ denote the indicator of success of the $i$-th Bernoulli trial. Then $X=\sum_{i=1}^n Y_i$. (Why?) Now use the Linearity of Expectation (FPS 7.7.6, 7.7.7) and Ex. 13.21.

13.208 HW (3 points) Let $\vt_A$ and $\vt_B$ denote the indicator variables of events $A$ and $B$, respectively. Prove that $\vt_A\cdot\vt_B=\vt_C$ for some event $C$. Describe $C$ as a very simple expression in terms of $A$ and $B$. No proof required.

13.210 HW (10 points) What is the expected number of Aces in a poker hand? Show all your work. State the size of your sample space. Make sure you give a clear definition of the probability space and the random variables you introduce; the definition of your random variables will account for half the credit.
Hint: indicator variables. The high point value indicates the importance of this problem, not the difficulty. The problem should be easy.

13.212 Bonus (10 points) FPS 7.7.16 (expected number of runs of $k$ heads in a sequence of $n$ coin flips). State the size of your sample space. Make sure you give a clear definition of the probability space and the random variables you introduce; the definition of your random variables will account for half the credit.   Hint: indicator variables. The high point value indicates the importance of this problem, not the difficulty. The problem should be easy.

13.214 HW (8+3 points, due Nov 25) FPS 7.7.22 (marbles in cups) For part (a), state the size of your sample space.
To evaluate a sequence $a_n$ asymptotically means to find the simplest expression $b_n$ that is asymptotically equal to $a_n$. For instance, if $a_n = (n^2-n+1)/(3n-8)$ then $b_n$ would be $n/3$.

13.216 HW (14 points, due Nov 25) FPS 7.7.18 (Club of 2000)

13.218 HW (3+2+4+4 points) Let us roll two dice. The first one shows the number $X$, the second one the number $Y$. (So $1\le X,Y \le 6$.) Determine (a) $E(X)$   (b) $E(X+Y)$   (c) $E(X^2)$   (d) $E(XY)$.   Show all your work. Express your answers as fractions in their simplest form (like $9/5$ if you get $18/10$). Do not use electronic devices.

Class 12, Thu 11-05   Problems due Monday, November 9, 11:59pm, except where stated otherwise. Proof required except where expressly stated otherwise.

12.10 DO   Prove: if $\fff$ is a number field then $\qqq\subseteq\fff$. (See DEF 11.50 for number fields.) Start with proving that $0,1\in\fff$.

12.15 NOTATION   Let $\fff$ be a number field. $\fff[x]$ denotes the set of polynomial over $\fff$, i.e., the set of polynomials with coefficients in $\fff$.

12.17 NOTATION FOR TODAY.   In all exercises below, $\fff$ will denote a number field. If you are not comfortable with complex numbers, think of $\fff$ being the real numbers.

12.20 DEF (divisibility)   Let $f,g\in \fff[x]$. We say that $g$ divides $f$ (notation: $g\mid f$) if $(\exists h\in\fff[x])(f=gh)$.

12.22 HW (4 points)   Let $k\ge 1$. Prove:   $x-1 \mid x^k-1$.

12.24 DO   Let $g\in\fff[x]$. Prove:   $(\forall f\in\fff[x])(g\mid f)$ if and only if $\deg(g)=0$, i.e., $g$ is a nonzero constant polynomial.

12.30 DIVISION THEOREM for polynomials over a number field.
$$(\forall f,g\in\fff[x], g\neq 0)(\exists! q,r\in\fff[x])((f=q\cdot g+r) \wedge (\deg(r) < \deg(g))$$ (Recall the notation:   $(\exists! q)$ means there exists a unique $q$, i.e., there exists exactly one $q$ such that $\dots$.)

12.32 Examples. Let $\fff=\qqq$ (the rationals).
If $f=x^3+3x+7$ and $g=x^2+x+1$ then $f=(x-1)\cdot g+(3x+8)$.   (DO: Verify!)
If $f=x^3+3x-7$ and $g=3x^2-2x-5$. Then $f=((1/3)x+(2/9))\cdot g+((46/9)x-(53/9))$.   (DO: Verify!)

12.34 HW (5 points)   Prove the uniqueness statement in the Division Theorem. What you need to show is this: If $f=q_1\cdot g+r_1 =q_2\cdot g+r_2$ and $\deg(r_1)<\deg(g)$ and $\deg(r_2)<\deg(g)$ then $q_1=q_2$ and $r_1=r_2$.

12.36 HW (6 points, due Mon, Nov 16)   Prove the existence statement in the Division Theorem. (Ignore uniqueness.) Fix the polynomial $g$ and proceed by induction of $\deg(f)$.

12.38 DO   In the Division Theorem, if $\deg(g)=1$ then $r$ is a constant.

12.40 HW (4 points)   Let $g=x-a$ be a monic linear polyomial $(a\in\fff)$. Apply the Division Theorem:   $f=(x-a)g+r$. Here $r\in\fff$ is a constant. Prove:   $r=f(a)$.

12.42 DEF   Let $f\in\fff[x]$ and $a\in \fff$. We say that $a$ is a root of $f$ if $f(a)=0$.
Example.   $a=-2$ is a root of the polynomial $f=x^3+3x^2+5x+6$.   (DO: Verify!)

12.44 HW (3+3 points)   (a)   Let $f\in\fff[x]$ and $a\in \fff$. Prove: $a$ is a root of $f$ if and only if $x-a\mid f$.   (b)   Consider the example in the preceding definition:   let $f=x^3+3x^2+5x+6$. We stated that $f(-2)=0$. Find the polynomial $g$ such that $f=(x+2)\cdot g$. State, do not prove.

12.46 DEF   Let $f\in\fff[x]$ and $a\in \fff$. We say that $a$ is a multiple root of $f$ if $(x-a)^2 \mid f$.

12.48 Bonus (5 points)   Prove: $a$ is a multiple root of $f$ if and only if $f(a)=f'(a)=0$. Here $f'$ denotes the derivative of $f$.

12.50 Bonus (5 points) Let $n\ge 2$ and $f=x^n+x+1$. Prove: $f$ does not have multiple roots among the complex numbers.

12.55 Bonus (5+5 points, due Mon, Nov 16) Let $a_0+a_1x+\dots+a_nx^n\in\zzz[x]$ be a polynomial with integer coefficients. Assume $a_n=1$, so $f$ is monic and $\deg(f)=n$.
(a) Prove: if $k\in \zzz$ is a root of $f$ then $k\mid a_0$.
(b) Prove: if a rational number $r$ is a root of $f$ then $r$ is an integer.

More about polynomials will be added later.

12.60 DEF (limit)  Let $a_n$ be an infinite sequence of real numbers and $L\in\rrr$. We say that the limit of $a_n$ (as $n$ approaches infinity) is $L$ if $$ (\forall \eps > 0)(\exists n_0)(\forall n)(n > n_0 \Rightarrow |a_n - L| < \eps)$$ In words, for every positive $\eps$, for all sufficiently large $n$, $a_n$ is within $\eps$ of our target $L$. Observe how we express "for all sufficiently large $n$" by quantifiers: there exists a threshold $n_0$ such that when $n$ exceeds that threshold then the desired effect happens.
[Update 11-08 1am: The word "infinite" was added in "infinite sequence" above. In all problems where we talk about the limit of as sequence as $n\to\infty$, it is tacitly assumed that the sequence is infinite.]

12.62 NOTATION. To express the fact defined in the preceding exercise, we write $$\lim_{n\to\infty} a_n = L \quad\text{ or simply }\quad a_n\to L.$$ We say "$a_n$ tends to $L$ as $n$ goes to infinity."
WARNING.   We cannot say that "the limit of $a_n$ tends to $L$." Only a sequence can tend to $L$, but the limit is a fixed number, not a sequence, so it does not go anywhere. For the same reason, we cannot write $\lim_{n\to\infty} a_n\to L$. (We use the verbs "tend" and "go" interchangeably in this context, but perhaps we say "go" more often if the limit is infinite.)

12.64 DEF (infinite limit)   Let $a_n$ be a sequence of real numbers. We say that the limit of $a_n$ (as $n$ approaches infinity) is $\infty$ if $$ (\forall K)(\exists n_0)(\forall n)(n > n_0 \Rightarrow a_n > K)$$

12.66 NOTATION. To express the fact defined in the preceding exercise, we write $$\lim_{n\to\infty} a_n = \infty\quad\text{ or simply }\quad a_n\to \infty.$$ We say "$a_n$ goes to infinity as $n$ goes to infinity."

12.68 DO   Analogously define $a_n\to -\infty$.

12.70 HW (4 points) Define what it means that the sequence $a_n$ does NOT go to infinity. Your definition should be a well-quantified formula with no English words. Any negation should only come after you finished all quantifiers, so statemenst like $\not\exists n_0$ ("there does not exist $n_0$") will not be accepted. No proof required.

12.72 DEF   We say that the sequence $a_n$ is increasing if $(\forall n)(a_n\le a_{n+1})$. The sequence is strictly increasing if $(\forall n)(a_n < a_{n+1})$.

12.74 DEF   We say that the sequence $a_n$ is eventually increasing if it increases for all sufficiently large $n$, i.e., if $$(\exists n_0)(\forall n)(n > n_0 \Rightarrow a_n \le a_{n+1})$$ We define eventually strictly increasing analogously.

12.76 HW (3 points) Find a strictly increasing sequence that does not go to infinity. Prove that your sequence does not go to infinity, based on the definition of infinite limit above (DEF 12.64).

12.78 HW (4 points) Find a sequence that goes to infinity but is not eventually increasing. No proof required.

12.80 HW (3 points, due Monday, November 16) Find a sequence that has no limit. No proof required.
[This problem was inadvertently omitted from the Nov 9 assignments.]

12.100 DEF   We say that the sequences $a_n$ and $b_n$ are asymptotically equal if $$ \lim_{n\to\infty} \frac{a_n}{b_n} = 1. $$ We denote this circumstance by   $a_n\sim b_n$.

12.102 DEF   We say that the sequence $a_n$ is eventually nonzero if $a_n\neq 0$ for all sufficiently large $n$, i.e., if $(\exists n_0)(\forall n)(n > n_0 \Rightarrow a_n\neq 0)$.

12.104 COMMENT   If $a_n\sim b_n$ then both of these sequences have to be eventually nonzero. The reason is that if $b_n$ is not eventually nonzero then infinitely many terms in the limit are undefined, and therefore the limit is undefined. If $b_n$ is eventually nonzero but $a_n$ is not then infinitely many of the quotients $a_n/b_n$ are zero, so the sequence cannot tend to $1$.

12.106 HW (1+2+2 points) Let ENZ denote the set of eventually nonzero sequences. Prove: asymptotic equality is an equivalence relation on ENZ.

12.110 DO   Prove:   $3n^5-17n^3-100n^2-83n+150 \sim 3n^5$.
Proof. $$\frac{3n^5-17n^3-100n^2-83n+150}{3n^5}= 1 - \frac{17}{3n^2} -\frac{100}{3n^3} - \frac{83}{3n^4}+\frac{150}{3n^5}$$ Since every term on the right-hand side, except the $1$, goes to zero, the entire exression goes to $1$.

12.112 DO   Every nonzero polynomial is asymptotically equal to its leading term. More precisely, let $f\in\rrr[x]$ be a polynomial of degree $k\ge 0$ with leading term $a_k x^k$. Prove:   $f(n) \sim a_k n^k$.

12.114 HW (5 points) Find two sequences, $a_n, b_n > 1$ such that $a_n/b_n \to \infty$ and $\ln a_n \sim \ln b_n$.

12.116 Bonus (5+5 points, due Mon, Nov 16) (a) Let $a_n, b_n > 1$. Prove that the following inference is false:   $a_n \sim b_n \Rightarrow \ln a_n \sim \ln b_n$
(b) Let $a_n, b_n > 1.01$. Prove:   $a_n \sim b_n \Rightarrow \ln a_n \sim \ln b_n$

Class 11, Tue 11-03   Problems due Monday, November 9, 11:59pm, except where stated otherwise.

11.06 Bonus (interval sums, 5+2 points)   (a)   Let $n\ge 1$. Consider a sequence $a_1,a_2,\dots,a_n$ of integers. Prove: there exist $k,\ell$ such that $1\le k\le \ell\le n$ and $\sum_{i=k}^{\ell} a_i\equiv 0 \pmod n$.
  (b)   Prove that the same statement with $n-1$ integers is false for every $n\ge 2$.

11.10 DEF (Strings)   Let $\Sigma$ be a finite set to which we refer to as the alphabet; the elements of $\Sigma$ will be called letters. A string of length $n$ over the alphabet $\Sigma$ is a function $w:[n]\to \Sigma$. We represent the function $w$ as a string of letters. The domain of this function, $[n]$, is the set of positions, and position $x$ is filled with entry $f(x)$.
Example: If $\Sigma=\{A,B,C\}$ and $w$ is defined by the table $$\begin{array}{|c||c|c|c|c|c|} \hline x & 1 & 2 & 3 & 4 & 5\\ \hline w(x) & C & A & C & B & B\\ \hline \end{array} $$ then we write the string as $w = CACBB$. Strings are also referred to as words.

11.12 DO   If $|\Sigma|=k$ then the number of strings of length $n$ over $\Sigma$ is $k^n$.

11.14 TERMINOLOGY   A necklace is just a string. The alphabet is the types of "beads" we can use in the string, e.g., $\Sigma=\{Red,Blue,Green\}$, or $\Sigma'=\{Ruby,Sapphire,Emerald\}$. We have an unlimited supply of each type of bead.

11.16 ROTATIONAL EQUIVALENCE.   We imagine that the beads are arranged in a circle at the corners of a regular $n$-gon, with $w(n)$ placed in the 12 o'clock position. We say that two necklaces are (rotationally) equivalent if we can rotate the $n$-gon to turn one necklace into the other. (See the pictures in the class notes.)

In this context it is more convenient to think of the domain (the set of positions) being $\{0,1,\dots,n-1\}$ (so $w(0)$ is placed at 12 o'clock). In this case we can say that the string $w':\{0,1,\dots,n-1\}\to\Sigma$ is a rotation of the string $w:\{0,1,\dots,n-1\}\to\Sigma$ by $t$ steps if $(\forall i\in\{0,\dots,n-1\})(w'((i+t\bmod m))=w(i))$.
Example.   Here are the successive rotations of the string $CACBB$:  $CACBB$, $BCACB$, $BBCAC$; $CBBCA$; $ACBBC$. One more rotation will bring us back to the starting string.

11.18 DO   Rotational equivalence is an equivalence relation on the set of strings of length $n$ over the alphabet $\Sigma$.

11.20 Bonus (5 points)   Prove: the size of each equivalence class is a divisor of $n$. Use Exercise 6.44 to give a proof in a couple of lines. Solutions that do not make essential use of 6.44 will not be accepted.

11.22 DO   The number of equivalence classes of size 1 is $k$ (the size of the alphabet).
Example. In the example above ($n=5$, $\Sigma=\{A,B,C\}$), the equivalence classes of size 1 are $\{AAAAA\}$, $\{BBBBB\}$, $\{CCCCC\}$.

11.24 DO   Count the equivalence classes when $n=p$ be a prime number.
Solution.   By 11.20, each equivalence class has size $1$ or $p$. By 11.22, the number of equivalence classed of size $1$ is $k$.
Let $M$ denote the number of equivalence classes of size $p$. This means the total number of necklaces is $k+Mp$. By 11.12, this number is $k^p$, so we have $k^p = k + Mp$. Solving for $M$ we obtain $$ M = \frac{k^p-k}{p} .$$

The total number of equivalence classes is $k+M$.

11.26 Counting proof of Fermat's little Theorem.   The number $M$ is an integer, so $p\mid k^p-k$, i.e., $k^p\equiv k\pmod p$. We proved Fermat's Little Theorem in all cases that matter (for every prime $p$ and every $k\ge 2$). FlT is trivial for $k=0$ and $1$. The next exercise completes our second proof of FlT.

11.28 DO   Let $p$ be a prime and $k\in\zzz$. Prove:   If $k^p\equiv k \pmod p$ then $(-k)^p\equiv -k \pmod p$.
(Do not use FlT.)

11.35 HW (Binomial proof of FlT, 5 points). Prove the statement $k^p\equiv k\pmod p$ for $k\ge 0$ by induction on $k$. Use the Binomial Theorem and Exercise 9.114.

11.37 A COMMENT ON THE PHILOSOPHY OF THE STUDY OF MATHEMATICS.   With the preceding exercise we shall have three entirely different proofs of Fermat's little Theorem. These proofs reveal different aspects of the theorem, and connect diverse lines of thought in surprising ways, underlining the unity of mathematics. More important than proving many theorems is to have several proofs of a small number of core results. FlT is such a core result. A more advanced core result of number theory is the Law of Quadratic Reciprocity, discovered by Gauss in 1796. Gauss attached such significance to this result, he produced six different proofs over a period of two decades. This website lists 246 proofs, the most recent one from 2013.

11.50 DEF   A number field is a subset $\fff$ of the complex numbers such that (a) $|\fff|\ge 2$ and (b) $\fff$ is closed under subtraction and division except for division by $0$. Examples of number fields: $\ccc$, $\rrr$ (the real numbers), $\qqq$ (the rational numbers).

11.52 DO   $\zzz$ is not a number field. Reason: not closed under division.

11.53 DO   The non-negative real numbers do not form a number field.

11.54 HW (5 points)   Let $\qqq[\sqrt{2}]$ denote the set $\qqq[\sqrt{2}]=\{a+b\sqrt{2} \mid a,b\in\qqq\}$. Prove that $\qqq[\sqrt{2}]$ is a number field.

11.60 DEF   A polynomial is an expression of the form $a_0+a_1x+\dots+a_nx^n$ where the coefficients $a_i$ are from a specified domain. The domains we consider are number fields. The set of polynomials with coefficients in the domain $\fff$ is denoted $\fff[x]$ (if the variable is denoted $x$; if the varible is denoted, say, $t$, we write $\fff[t]$ for the set of polynomials). So we shall especially consider the following sets of polynomials: $\ccc[x]$, $\rrr[x]$, $\qqq[x]$.

11.62 DEF, continued.   Two polynomials are considered to be the same if they only differ in term with ocefficient zero. So, for insatance, $7+3x-5x^2 = 7+3x-5x^2 +0x^3$. The degree of the term $a_kx^k$ is $k$, unless $a_k=0$. The leading term in a polynomial is the highest-degree term with a non-zero coefficient, and its degree is the degree of the polynomial. So the degree of the polynomial $f(x)=7+3x-5x^2 +0x^3$ is $\deg(f)=2$, its leading term being $-5x^2$. A polynomial is monic if its leading term has coefficient 1.

11.64 DEF   The degree of the zero polynomial (all coefficients zero) is defined to be $\deg(0)=-\infty$.

11.66 DO   Let $f,g$ be polynomials over a number field. Prove: if $fg=0$ (the zero polynomial) then $f=0$ or $g=0$.

11.68 DO   Let $f,g$ be polynomials over a number field. Prove:   (a)   $\deg(fg)=\deg(f)+\deg(g)$, and (b)   $\deg(f+g)\le \max\{\deg(f),\deg(g)\}$.   How does our convention about the degree of the zero polynomial work in these rules?

11.70 DO   The polynomials of degree zero are exactly the nonzero constant polynomials $f(x) =a_0 \neq 0$.

11.72 DEF   A linear polynomial is a polynomial of degree $1$.

11.74 DEF   A quadratic polynomial is a polynomial of degree $2$.

Class 10, Thu 10-29  

10.02 STUDY Pascal's triangle from web sources.

10.03 ART PROJECT   Study Pascal's triangle modulo 2.   What makes this and art project?

10.05 Binomial Theorem, version 1:   For $n\ge 0$ we have $$ (1+x)^n = \sum_{k=0}^n \binom{n}{k} x^k $$ Example:  $(1+x)^4=1+4x+6x^2+4x^3+x^4$.

10.06 Binomial Theorem, version 2:   For $n\ge 0$ we have $$ (x+y)^n = \sum_{k=0}^n \binom{n}{k} x^ky^{n-k} $$ Example:  $(x+y)^4=x^4+4x^3y+6x^2y^2+4xy^3+y^4$.

10.07 DO   (a)   Observe that version 1 is a special case of version 2.   (b)   Deduce version 2 from version 1.
So the two versions are equivalent. [I find version 1 much more often useful.]

10.08 DO   Deduce version 1 from Exercise 5.76: $$\prod_{i=1}^n (1+x_i) = \sum_{A\subseteq [n]} \prod_{i\in A}x_i.$$

10.09 DO   Prove:   $\sum_{k=0}^n \binom{n}{k} = 2^n$. Give two proofs: (1)   a combinatorial proof (by counting subsets, using the definition of the binomial coefficients)   (2) an algebra proof, using the Binomial Theorem.

10.10 DO   Evaluate   $\sum_{k=0}^n (-1)^k \binom{n}{k}$.
Answer: the sum is $0$ for $n\ge 1$ and $1$ for $n=0$. Give two proofs of these statements, a combinatorial proof and an algebra proof.

10.11 HW   Let $S(n,r)=\sum_{k=0}^{\infty} \binom{n}{kr}$.
Given $n\ge 0$ and $r\ge 1$, determine the number of non-zero terms in this sum. Your answer should be a very simple expression in terms of $n$ and $r$. Briefly reason your answer.

10.12 DO   Prove: $S(n,2)= \frac{2^n}{2}$ for all $n$ with one exception. What is the exception? Use the Binomial Theorem in your proof. Hint: Show that $2S(n,2)=(1+1)^n + (1-1)^n$.

10.13 HW (3 points, due Mon, Nov 9)   Prove:   $\displaystyle{(\forall n\ge 0)\left(S(n,3)\neq \frac{2^n}{3}\right)}$. Make essential reference to the Prime Property Theorem.

10.14 Bonus (7 points, due Wed, Nov 25) Prove:  $\displaystyle{(\forall n\ge 0)\left(\left|S(n,3)-\frac{2^n}{3}\right| < 1\right)}$.   Use the Binomial Theorem, version 1, for an elegant proof. (Hint: Generalize the proofs of Exercises 10.10 and 10.11. Use complex numbers.)

10.15 HW (4 points, due Mon, Nov 9) Let $0\le k\le n$ and let $f(n,k)$ denote the number of those $n$-subsets $B$ of $[2n]$ which satisfy $|B\cap [n]|=k$. Give a very simple closed-form expression for $f(n,k)$, using binomial coefficients. Prove your answer using the definition of the binomial coefficients.

10.16 Bonus (4+4 points, due Mon, Nov 16) Prove, for all $n\ge 0$, that $$ \sum_{k=0}^n \binom{n}{k}^2 = \binom{2n}{n}\,. $$ Give two proofs:  (a)   a combinatorial proof and  (b)  an algebra proof.
Hint for the combinatorial proof:   $\binom{2n}{n}$ counts the $n$-subsets of $[2n]$. Count them in a different way, using the preceding exercise.
Hint for the algebra proof:   $(1+x)^{2n}=(1+x)^n\cdot(1+x)^n$. Compare the coefficients of $x^n$ on each side.
[Update 11-09 6:40pm: submission date moved from Nov 9 to Nov 16]

10.17 HW+Bonus (due Mon, Nov 9) A function $f: [k]\to [n]$ is increasing is $(\forall x,y)(x\le y \Rightarrow f(x)\le f(y))$. Increasing functions are also called nondecreasing to avoid confusion with "strictly increasing" functions. We say that $f$ is strictly increasing if $(\forall x,y)(x < y \Rightarrow f(x) < f(y))$.
HW (a) (4 points) Given $k,n\ge 0$, count the strictly increasing functions $f:[k]\to [n]$. Your answer should be a very simple formula involving binomial coefficients. Briefly reason your answer.
Bonus (b) (5 points) Given $k,n\ge 0$, count the nondecreasing functions $f:[k]\to [n]$. Use the result of (a).   Your answer should be a very simple formula involving binomial coefficients. Prove your answer, using a correct answer to (a). The reduction of (b) to (a) should be very simple. Elegance counts. If your solution does not make essential use of part (a), you get at most 3 points.

10.20 DO   Assume $a\equiv b \pmod m$ and $k\mid m$. Then $a\equiv b\pmod k$. Show that this follows from the transitivity of divisibility.

10.22 THEOREM (Solvability of linear congruences) Let $a,b,m\in \zzz$. The congruence $ax\equiv b \pmod m$ is solvable if and only if $\gcd(a,m) \mid b$.

10.24 HW (1+4 points, due Mon Nov 16) Prove the necessity of the condition $\gcd(a,m)\mid b$ using 10.20. Include a proof of 10.20. Your proof, including the proof of 10.20, should be just a couple of lines.
[11-6:Submission date was postponed by a week, from Nov 9 to Nov 16]

10.26 HW (4 points, due Mon Nov 16) Prove the sufficiency of the condition $\gcd(a,m)\mid b$ using Bézout's lemma.
[11-6:Submission date was postponed by a week, from Nov 9 to Nov 16]

10.28 DO   Let $a,b,m,d\in\zzz$. Assume $d\neq 0$ and $d$ is a common divisor of $a,b,m$. Then the following two statements are equivalent:   (1)   $a\equiv b\pmod m$   (2) $(a/d) \equiv (b/d) \pmod{m/d}$.

10.30 Bonus (5 points, due Mon Nov 9) Let $a,b,m\in\zzz$. Assume $\gcd(a,m)=1$. Let $S=\{x\in\zzz\mid ax\equiv b\pmod m\}$. We know from Theorem 10.22 the $S\neq \emptyset$. Prove: $S$ is a residue class mod $m$. More precisely, prove that if $x_0\in S$ then $(\forall x)((ax\equiv b\pmod m)\Leftrightarrow(x\equiv x_0\pmod m)$.

10.32 EXAMPLE Solve the congruence $42x\equiv 30 \pmod{117}$.
First we notice that $3$ is a common divisor of $42$, $30$, and $117$, so we divide each of them by $3$:
$14x\equiv 10\pmod{39}$. The preceding exercise says this congruence is equivalent to the original one. We add the observation that $39x\equiv 0 \pmod{39}$ and use Euclid's algorithm on the left-hand side with some short-cuts:
     (1)   $14x \equiv 10 \pmod{39}$
     (2)   $39x \equiv 0 \pmod{39}$
Multiply (1) by 3:
     (3)   $42x \equiv 30 \equiv -9 \pmod{39}$
Subtract (2) from (3):
     (4)   $ 3x \equiv -9 \pmod{39}$
Multiply (4) by 5:
     (5)   $15x \equiv -45 \equiv -6 \pmod{39}$
Subtract (1) from (5):
     (6)   $ x \equiv -16 \pmod{39}$

What we have proved so far is that if there is a solution $x$ then $x\equiv -16 \pmod{39}$. To complete the solution, we can do one of two things.
     (A)  Verify that if $x\equiv -16 \pmod{39}$ then $14x\equiv 10 \pmod{39}.$ Indeed, $14x\equiv 14\cdot(-16)=-224\equiv 10$, because $234=39\cdot 6$. So this required some calculation.
     (B)  By THEOREM 10.22, a solution exists. Let $z$ be a solution. We proved that $z\equiv -16\pmod{39}$. By 10.30 we know that the set of solutions is the set $z+39\zzz$ (the mod 39 reside class that includes $z$) but this residue class also includes $-16$, so $-16$ is a solution. We reached this conclusion with no calculation at all.
WARNING. Method (B) only works if we did not make an error in calculating that $x$ must satisfy $x\equiv -16 \pmod{39}$. To guard against potential errors, method (A) is preferable.

10.40 HW (6 points) Use the method in 10.32 to solve the congruence $27x\equiv 47 \pmod{101}$. Show all your work. Find all solutions.

10.42 DO   Prove, for all integers $m,x,y$, that $m\zzz+x = m\zzz+y$ if and only if $x\equiv y\pmod m$.

10.45 DEF   We say that $x$ is a multiplicative inverse of $a$ modulo $m$ if $ax\equiv 1 \pmod m$.
Examples.   $7$ is a multiplicative inverse of $8$ modulo $11$ because $8\cdot 7 = 56 \equiv 1 \pmod{11}$.   $-4$ is also a multiplicative inverse of $8$ modulo $11$.

10.46 HW (2 points)   Prove:   $85$ does not have a multiplicative inverse modulo $731$. Show all your work.

10.47 DO   Prove:  If $x$ is a multiplicative inverse of $a$ modulo $m$ and $y\equiv x\pmod m$ then $y$ is a multiplicative inverse of $a$ modulo $m$.

10.48 HW (3 points, due Mon, Nov 9)   Prove the converse of the preceding exercise: If both $x$ and $y$ are multiplicative inverses of $a$ modulo $m$ then $x\equiv y\pmod m$.

10.50 DO   If $x$ is a multiplicative inverse of $a$ modulo $m$ then the set of multiplicative inverses of $a$ modulo $m$ is the residue class $m\zzz+x$.

10.52 NOTATION   $(a^{-1} \bmod m)$ denotes the smallest non-negative multiplicative inverse of $a$ modulo $m$ (if a multiplicative inverse exists).
Examples.   $(8^{-1} \bmod{11})=7$.   $(8^{-1} \bmod{-11})=7$.   $((-8)^{-1} \bmod{11})=4$. (Verify!)

10.54 HW (3+3 due Mon, Nov 9)   Prove: the integer $a$ has a multiplicative inverse modulo $m$ if and only if $\gcd(a,m)=1$.   You may use without proof a previous exercise. State which exercise you are using.

10.56 DO   Use the method of Exercise 10.32 to find $(55^{-1} \bmod 89)$.

10.58 Bonus (5 points, due Mon, Nov 9)   Let $n\ge 2$. Find $(F_n^{-1} \bmod F_{n+1})$. Your answer should be a very simple expression in terms of Fibonacci numbers. ($F_n$ denotes the $n$-th Fibonacci number.)

10.60 Bonus (4 points, due Mon, Nov 9)   Given $k\ge 1$, find $(k^{-1} \bmod{2k+1})$. Prove your answer. Tell us how you found it.

10.62 HW (5 points, due Mon, Nov 9)   Let $p$ be a prime number. Find all values of $x$ such that $x=(x^{-1} \bmod p)$. Prove your answer. Use the prime property.

More to follow. Please check back later. REFRESH each time you check this page.

Class 9, Tue 10-27   Reduced residue classes modulo $m$, reduced set of residues. Euler-Fermat congruence, with proof. First proof of Fermat's little Theorem. Permutations. Counting equivalence classes: King Matthias's shepherd's method. Counting anagrams. Binomial coefficients.
Problems due Monday, Nov 2, along with the set of problems from Class 8.

9.10. REVIEW equivalence relations. Given an equivalence relation $R$, the equivalence classes of $R$ are the blocks of the partition $\Pi_R$ corresponding to $R$ (DEF 8.78). A system of representatives for $R$ is a set that consists of one member from each equivalence class (DEF 8.88).

9.12 REVIEW   The modulo $m$ residue classes are the equivalence classes of the mod $m$ congruence (DEF 8.90). So $x,y\in\zzz$ belong to the same residue class mod $m$ if and only if $x\equiv y \pmod m$.

9.14 DO   For $m\ge 1$, the mod $m$ residue classes are the sets $m\zzz$, $m\zzz+1$, $m\zzz+2$, $\dots$, $m\zzz+(m-1)$.
[Typo corrected 10-31 12:10pm]

9.16 REVIEW   A set of representatives of the mod $m$ residue classes is called a complete set of residues mod $m$ (DEF 8.92).

9.18 REVIEW problems 8.102 and 8.104.

9.20. DEF   Recall: we say that $a,b\in\zzz$ are relatively prime if $\gcd(a,b)=1$.

9.22 DO   Let $S$ be a mod $m$ residue class. Prove: if some element of $S$ is relatively prime to $m$ then all elements of $S$ are relatively prime to $m$. Use HW 8.10.

9.24 DEF   Let $S$ be a residue class modulo $m$. We say that $S$ is a reduced residue class modulo $m$ if the elements of $S$ are relatively prime to $m$.

9.26 REVIEW Euler's $\vf$ function (DEF 5.52) and the exercises about this function.

9.28 DO   Let $m\ge 1$. Prove: the number of reduced residue classes mod $m$ is $\vf(m)$.

9.30 DEF   A reduced set of residues mod $m$ is a set of representatives of the reduced residue classes mod $m$.

9.32 DO   Let $m\ge 1$. Prove: the numbers $r_1,\dots,r_{\vf(m)}$ form a reduced set of residues if and only if the following conditions hold:
(1)   $(\forall i)(\gcd(r_i,m)=1)$ and (2)   $(\forall i,j)((r_i\equiv r_j \pmod m)\Rightarrow (i=j))$.

9.34 DO   Recall that $\vf(36)=\vf(4)\vf(9)=2\cdot 6=12.$ Prove that the set $\{\pm 1,\pm 5,\pm 7,\pm 11,\pm 13, \pm 17\}$ is a reduced set of residues mod $36$.

9.36 HW (3+3+3) Which of the following sets are reduced sets of residues modulo $36$? In each case answer YES or NO (YES meaning it is). Prove your answers. You may use any of the exercises above and in previous sections without proof. Your proofs of the "NO" answers should be very short -- half a line each. Prove your "YES" answers by providing a bijection between the given set and the reduced set of residues stated in the preceding exercise such that corresponding numbers are in the same residue class mod $36$.
(a)   $\{-113,-65,-19,-17,-1,1,5,29,49,59,105,169\}$
(b)   $\{-77,-65,-31,-19,-17,-1,29,37,49,83,95,133\}$
(c)   $\{-65,-19,-1,5,19,31,37,47,53,61,65,95\}$

9.38 HW (4 points) Give a list of prime numbers that constitute a reduced set of residues modulo $36$. Note that we defined prime numbers to be positive, so your list should consist of positive numbers. Prove the correctness of your list by providing a bijection between your set of primes and the reduced set of residues stated in 9.34 such that corresponding numbers are in the same residue class mod $36$.

9.40 Bonus (4 points) Prove that for every $m\ge 1$ there is a list of positive composite numbers that constitutes a reduced set of residues modulo $m$.

9.42 Bonus (6 points) Based on a result stated but not proved earlier in these notes, prove that for every $m\ge 1$ there is a list of primes that constitutes a reduced set of residues mod $m$.

9.44 CH   Let $m\ge 3$. Prove that no list of squares can be a reduced set of residues mod $m$.

9.45 DO   Find a reduced set of residues mod $7$ that is a geometric progression.

9.46 CH$^*$   Prove: if $p$ is a prime number then there is a geometric progression that is a reduced set of residues mod $p$.

9.50 DO   Let $r_1,r_2,\dots,r_{\vf(m)}$ be a reduced set of residues mod $m$ and let $\gcd(a,m)=1$. Then $ar_1,ar_2,\dots,ar_{\vf(m)}$ is also a reduced set of residues mod $m$.
Hint. Use 9.32 and the Cancellation Law for congruences (7.30).

9.52 DO   Let $m\ge 1$. Let $r_1,\dots,r_{\vf(m)}$ and $s_1,\dots,s_{\vf(m)}$ be two reduced sets of residues mod $m$. Prove: $$\prod_{i=1}^{\vf(m)} r_i \equiv \prod_{i=1}^{\vf(m)} s_i\pmod m$$

9.54 Euler-Fermat congruence. Let $m\neq 0$. If $\gcd(a,m)=1$ then $$ a^{\vf(m)}\equiv 1 \pmod m$$

9.56 REVIEW the proof of this theorem from class. WLOG $m\ge 1$. Let $r_1,\dots,r_{\vf(m)}$ be a reduced set of residues modulo $m$. Let $s_i=ar_i$. By Ex. 9.50, the $s_i$ also form a reduced set of residues mod $m$. Therefore, by Exercise 9.50 we have $\prod_{i=1}^{\vf(m)} r_i \equiv \prod_{i=1}^{\vf(m)} s_i \pmod m$. But $\prod_{i=1}^{\vf(m)} s_i = a^{\vf(m)}R$ where $R:=\prod_{i=1}^{\vf(m)} r_i$. So we have $R\equiv a^{\vf(m)}R \pmod m$. DO: prove that $\gcd(R,m)=1$. Now, by the Cancellation Law, we conclude that $1\equiv a^{\vf(m)}\pmod m$.   QED

9.58 DO   Deduce Fermat's little Theorem from the Euler-Fermat congruence. (Recall: if $p$ is a prime then $\vf(p)=p-1$.) This completes our first proof of FlT.

9.62 EXAMPLE   Assume $\gcd(a,697)=1$. Then $a^{640}\equiv 1 \pmod{697}$.
Proof.   $697=17\cdot 41$; these two factors are primes. Therefore $\vf(697)=\vf(17)\cdot\vf(41)=16\cdot 40=640$ and the result follows from the Euler-Fermat congruence.

9.64 HW (6+2 points) (a)   Assume $\gcd(a,697)=1$. Then $a^{80}\equiv 1\pmod{697}$.   (b)   This result is stronger than the preceding example. Why, in what sense is it stronger?
Hint to part (a). Note: $697=17\cdot 41$. First prove that $a\equiv b\pmod{697}$ if and only if $a\equiv b\pmod{17}$ and $a\equiv b\pmod{41}$. Then use FlT mod 17 and mod 41.

9.70 RECALL DEF   A permutation of a set $A$ is a bijection $f : A\to A$. If $|A|=n$ then the number of permutations of $A$ is $n! := \prod_{i=1}^n i$. Note:   $0!=1$ (empty product).

9.75 DO: COUNTING EQUIVALENCE CLASSES.   Let us consider an equivalence relation $R$ on the set $\Omega$. Let $\Pi_R=(B_1,\dots,B_m)$ denote the corresponding partition, so the $B_i$ are the equivalence classes. Assume all equivalence classes have equal size $b=|B_i|$. Then the number of equivalence classes is $$ m= \frac{|\Omega|}{b} .$$

9.80 King Matthias's shepherd's method. King Matthias of Hungary (1443-1490) was the last great king of the country before the country's conquest by the Ottomans (1541-1699). Matthias was elected (!) king in 1458, at the age of 14, while imprisoned in Prague by the King of Bohemia. Having been ransomed out of captivity, he immediately took the country's reins. During the harrowing times that followed Matthias's death, his reign was remembered fondly, legends were spun around his character that are told to this day. He is said to have wandered far and wide across his realm in disguise, discovering injustice and meting out justice against those who abused their power. He would also travel around the land with his royal entourage, meeting very clever "simple" people and humbling his nobles who could not match their wits. Here is an unofficial item of the latter genre.

9.82 A fable for students of mathematics.
During one of his tours of the country, King Matthias encountered a shepherd watching over his flock. "Hey, shepherd," the King asked, "how many sheep are there in your flock?" The shepherd bent down as if looking under the bellies of his sheep, then stood up, and said, "387, Your Grace." "Did you just count them? How did you do that so quickly?", the King inquired. "Very simple, Your Grace. I counted their legs, and divided that number by four."

9.84 The method. While few shepherds would use this method of counting, mathematicians do it all the time. Here is the method. We have a set $S$ of objects to be counted (such as the sheep in the flock). We define a larger set $L$ (such as the legs of the sheep) which we somehow know how to count. We define an equivalence relation on $L$ with the following two properties:   (1)   there is a bijection between the set $\Pi$ of equivalence classes and the set $S$   (2)   all equivalence classes have the same size $b$ which is known to us.
Under these conditions, obviously, $\displaystyle{|S|=\frac{|L|}{b}}$.

9.86 HW (3 points)   What was the equivalence relation on the legs that the shepherd employed? What are the equivalence classes of that relation? What is the size of each equivalence class? What is the number of equivalence classes?

9.88 Counting anagrams ("permutations with repeated entries").
Words put together from the same letters are called anagrams. For instance, an anagram for "DISCRETE" is "SECRET ID" (without the space).
We shall now use King Matthias's shepherd's method to count anagrams.
We are given $n$ Scrabble pieces, each having one of the letters $A$, $B$, or $C$ written on them. There are $k$ pieces with the letter $A$, $\ell$ pieces with the letter $B$, and $m$ pieces with the letter $C$, so $n=k+\ell+m$. Question: how many words can we put together out of these $n$ pieces. (All pieces must be used, and the "words" don't need to make sense.) For instance, if we have 3 $A$'s, 2 $B$'s, and 2 $C$'s, then some of the words we get are $AAABBCC$, $CABBACA$, $ABACCAB$.

9.90 Solution. Let us start with the "standard" word that lists the $A$'s first, then the $B$'s, and then the $C$'s (as in our first example). Let us call this word $w$. Let $L$ be the set of all the $n!$ permutations. Each permutation, applied to $w$, gives us an anagram. Let us say that two permutations $f,g$ are equivalent if they produce the same anagram. It should be clear that   (1)   this is an equivalence relation on $L$; and   (2)   the number of anagrams is the number of equivalence classes, and the size of each equivalence class is $k!\ell!m!$, corresponding the the permutations that permute all the $A$'s, all the $B$'s, and all the $C$'s independently, without mixing the letters. Therefore, the number of anagrams is $$ \frac{n!}{k!\ell!m!}\,. $$

9.91 HW (4 points, due Monday, Nov 9) Describe function of which the kernel corresponds to the equivalence relation defined in Solution 9.90. ("Corresponds" means the kernel is the partition defined by the equivalence relation.) While there are infinitely many functions with the same kernel, you should find the one that is natural in the context.
[This problem was inadvertently left out of the 10-02 HW sets.]

9.92 DO   Generalizing the preceding example, let us now have $t$ letters, $A_1,\dots,A_t$, and let $k_i$ be the number of occurrences of $A_i$, to which we refer as the multiplicity of $A_i$. We can even include letters we don't use; in that case, we would have multiplicity $k_i=0$. Now the number of anagrams is $$ \frac{n!}{\prod_{i=1}^t k_i!} $$ and $\displaystyle{n = \sum_{i=1}^t k_i}$.

9.94 DEF   An $n$-set is a set of $n$ elements. A $k$-subset is a subset with $k$ elements.

9.96 DEF   Let $n,k\ge 0$. The number of $k$-subsets of an $n$-set is denoted $\binom{n}{k}$, called a binomial coefficient.

EXAMPLES.   $\binom{n}{0}=1$   (there is exactly one empty set)
         $\binom{n}{1}= n$   (why?)
         $\binom{n}{n} = 1$   (an $n$-set has exactly one $n$-subset, namely, itself)
         if $k > n$ then $\binom{n}{k}=0$

9.98 DO   Prove:   If $0\le k\le n$ then $\binom{n}{k}=\binom{n}{n-k}$. Give a "bijective proof," i.e., a proof that constructs a bijection between two sets that are counted by the two sides of the equation.

9.100 DO (Pascal's identity)   Prove: if $n,k\ge 1$ then $$ \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k} .$$ Do not evaluate the binomial coefficients. Count the $k$-subsets of an $n$-set in two different ways.

9.102 DO   Find a bijection between the set of $k$-subsets of an $n$-set and the anagrams made of $k$ copies of $A$ and $n-k$ copies of $B$. According to the preceding exercises, this will prove that for $0\le k\le n$ we have $$ \binom{n}{k} = \frac{n!}{k!}{(n-k)!} $$

9.104 DO   Canceling the terms in the numerator that correspond to $(n-k)!$ we get the following formula: $$ \binom{n}{k} = \frac{n(n-1)\cdots(n-k+1)}{k!} \,.$$

9.106 DO   Prove that the formula in the preceding exercise is valid   (a)   if $k=0$, and also   (b)   if $k > n$.

9.108 EXAMPLES:   $\displaystyle{\binom{n}{1} = n}$,         $\displaystyle{\binom{n}{2} = \frac{n(n-1)}{2}}$,         $\displaystyle{\binom{n}{3} = \frac{n(n-1)(n-2)}{6}}$.

9.110 DO   Prove:   If $0\le k\le n$ then $\displaystyle{\binom{n}{k}\le \frac{n^k}{k!}}\,.$

9.112 HW (5 points, due Mon, Nov 16)   Let $1\le k \le n$. Prove: $$ \binom{n}{k} \ge \left(\frac{n}{k}\right)^k \,.$$ [11-6:Submission date was postponed by a week, from Nov 9 to Nov 16]

9.114 HW (5 points)   Let $p$ be a prime number and $1\le k \le p-1$. Prove that $\binom{p}{k}$ is divisble by $p$. Do not use the argument that "$p$ does not cancel" (we have not discussed what that really means); instead, use the Prime Property Theorem (Theorem 6.86, see DEF 6.72).

Class 8, Thu 10-22   Division Theorem. Euclid's Algorithm accelerated via the Division Theorem. Free variables and bound variables in a formula. Equivalence relations. Partitions. Preimage. Kernel of a function. Role of partitions (clustering objects) in concept formation. Fundametal Theorem of Equivalence Relations: partitions are defined by equivalence relations. Key role of equivalence relations in concept formation and (human and artificial) intelligence. System of representatives. Modulo $m$ residue classes. Complete set of residues modulo $m$. All homework assigned in this section is due Monday, November 2.

8.10 HW (4 points, due Mon, Nov 2)   Prove: $(\forall a,b,m)((a\equiv b\pmod m)\Rightarrow (\gcd(a,m)=\gcd(b,m)))$.

8.12 REVIEW the Euclid's algorithm handout (to be referred to as EUCL below). Solve the exercises in EUCL.

8.14 DO   Prove the Division Theorem (EUCL 1.13).

8.16 REVIEW the notation $(a \bmod m)$ (the smallest nonnegative residue modulo $m$). (EUCL 1.14) Let $m\neq 0$. The notation $(a \bmod m)$ denotes the smallest $r\ge 0$ such that $a\equiv r \pmod m$. This is the value $r$ that appears in the Division Theorem:   $a=mq+r$. The notation $(a \bmod m)$ in undefined for $m=0$.

8.18 REVIEW the accelerated version of Euclid's algorithm, using the Division Theorem (EUCL, Section 2). From this point on, when referring to Euclid's algorithm, we always refer to this accelerated version.

8.20 DO EUCL 2.2:   Prove the correctness of the algorithm using the loop invariant stated in EUCL 2.2.

8.22 HW (efficiency of Euclid's algorithm) (4+3 points, due Mon Nov 2).   EUCL 2.3 (a) (b).

8.40 DEF   A partition of a set $A$ is a representation of $A$ as the union of non-empty disjoint sets. We write $\Pi=\{B_1,\dots,B_k\}$ for the partition $A=B_1\dot\cup\dots\dot\cup B_m$ where the dots indicate that these sets are pairwise disjoint. The $B_i$ are called the blocks of $\Pi$.

8.41 Example.   The set $[3]$ has 5 partitions: $\Pi_1=\{\{1,2,3\}\}$,   $\Pi_2=\{\{1,2\},\{3\}\}$,   $\Pi_3=\{\{1,3\},\{2\}\}$,   $\Pi_4=\{\{2,3\},\{1\}\}$,   $\Pi_5=\{\{1\},\{2\},\{3\}\}$.

8.42 DEF   Let $f:A\to B$ be a function. The preimage of $b\in B$ is the set $f^{-1}(b) :=\{a\in A \mid f(a)=b\}$.
Example: Let $g:\rrr\to\rrr$ denote the function $g(x)=x^2$. Then $g^{-1}(4)=\{-2,2\}$,   $g^{-1}(0)=\{0\}$,   $g^{-1}(-1)=\emptyset$.

8.43 DO   Let $f:A\to B$ be a function and $b\in B$. Observe that   $f^{-1}(b)\neq\emptyset$ if and only if $b\in\range(f)$.
"Observe" means "notice that it follows immediately from the definition."

8.44 DEF   (Kernel of a function) A function $f:A\to B$ defines a partition $\Pi_f$ of the domain of $f$ as follows: $$\Pi_f = \{f^{-1}(b)\mid b\in \range(f)\}$$ The partition $\Pi_f$ is called the kernel of the function $f$.

8.45 EXAMPLE: Concept formation.   Let $A$ be a set of small plastic toy bears, each of them colored red, orange, yellow, green, blue, or purple. Let $B$ be the set of colors and $h:A\to B$ the function that assigns to each bear its color. Then $h^{-1}(\text{blue})$ is the set of blue bears, etc., and $\Pi_h$ is the partition of the bears according to their color.
There is an actual toy where 72 small plastic bears, identical except for their color, are accompanied by a set of plastic cups, one of each color. The parents pour the bears on the table, and the toddler's task is to sort the bears into the cups by color, i.e., to produce the preimage of each color under the function $h$ and thereby create the partition $\Pi_h$. The toddler's success demonstrates their grasp of the concept of "color" even while they may not yet have the words for the colors. Your instructor watched in amazement as their 18-month-old daughter rapidly solved the puzzle even before we, the parents, figured out what the task was; and we would not have had any way to explain the task to her, had she not figured it out herself. It took several more months before she learned the words "red," "blue," etc.   This example shows the critical role of partitions (clustering objects) in intelligence, both human and artificial.

8.46 DO   Let $f:A\to B$ be a function. Observe that $x,y\in A$ belong to the same block of the kernel of $f$ if and only if $f(x)=f(y)$.
Example: Two toy bears go into the same cup if and only if they have the same color.

8.47 DO   Verify that $\Pi_f$ is indeed a partition, i.e., $$A=\dot\bigcup_{b\in\range(f)} \ f^{-1}(b)\,.$$ Example: What this exercise says about the toy is that every bear goes into exactly one cup.

8.48 HW (4 points, due Mon, Nov 2)   Prove that every partition is the kernel of some function. More formally, prove the following. Given a partition $\Pi$ of the set $A$, there exists a set $B$ and a function $f:A\to B$ such that $\Pi = \Pi_f$.
COMMENT. This exercise asks you to perform one of the basic tasks of intelligence: naming the blocks of a partition. Different languages have different words for "red," "blue," etc., but all of them solve precisely this exercise in relation to the partition of objects by color (the partition $\Pi_h$).

8.50 DEF   Given a partition $\Pi=\{B_1,\dots,B_k\}$ of the set $A$, define the relation $R_{\Pi}$ as follows: for $a,b\in A$ we say that $a R_{\Pi} b$ if $(\exists i)(a,b\in B_i)$, i.e., $a$ and $b$ belong to the same block of the partition.

8.52 HW (4 points, due Mon Nov 2)   Prove: $R_{\Pi}$ is an equivalence relation.

8.56 DEF   The $n$-th Bell number $B(n)$ is defined as the number of partitions of $[n]$.

8.58 DO   Verify: $B(0)=1$, $B(1)=1$, $B(2)=2$, $B(3)=5$.

8.60 HW (5 points, due Mon, Nov 2) Prove:   $B(n)\le n^n\,.$ Give a very simple surjective solution: find a surjection that maps the set $[n]^{[n]}$ (the set of $[n]\to [n]$ functions) onto the set of partitions of $[n]$. Give a clear definition of your surjection. Do not prove that it is indeed a surjection.

8.62 Bonus (6 points, due Monday, Nov 2) Prove:   $B(n)\le n!$
Find an injective solution: give an injection from the set of partitions of $[n]$ to the set of permutations of $[n]$. Give a clear definition of your injection. Do not prove that it is indeed an injection.
A solution to this problem does not earn you credit for 8.60; you need to separately execute the instruction in 8.60 to earn credit for that problem.

8.64 Bonus (6 points, due Mon, Nov 2) Prove:   If $0\le k\le n$ then $B(n) \ge k^{n-k}$. Give an injective solution: construct an injection from the set $[k]^{[n-k]}$ to the set of partitions. What you need to do is assign a partition to each function $f:[n-k]\to [k]$ such that distinct functions do not collide (they are not assigned the same partition). Give a clear definition of your injection. Do not prove that it is indeed an injection.

8.70 (Partitions vs. equivalence relations)   Recall that a partition $\Pi=\{B_1,\dots,B_k\}$ of a set $A$ defines an equivalence relation $\sim_{\Pi}$ on $A$ by the rule that for $a,b\in A$ we write $a\sim_{\Pi} b$ if $a$ and $b$ belong to the same block of the partition, i.e., if $(\exists i)(a,b\in B_i)$.

8.72 DO (uniqueness of partition)   Prove: Different partitions define different equivalence relations. In other words, let $\Pi$ and $\Psi$ be two partitions of the set $A$. Prove: if $\sim_{\Pi} = \sim_{\Psi}$ then $\Pi = \Psi$.

8.74 Fundamental Theorem of Equivalence Relations Let $\sim$ be an equivalence relation on the set $A$. Then $\sim$ arises from a unique partition. In other words, $(\exists!\text{ partition }\Pi\text{ of }A)(\sim = \sim_{\Pi})$.

8.75 COMMENT   The uniqueness part of the statement is the content of Exercise 8.72. The non-trivial part is the existence.

8.78 DEF   The blocks of $\Pi$ are called the equivalence classes of the relation $\sim$.
With these classes in mind, we can informally summarize the Theorem as saying that equivalence relations classify.
This result is fundamental to understanding how intelligent beings create concepts such as numbers, colors, etc. Natural numbers arise from the observation that certain pairs of sets have a bijection between them, and this relation among sets is an equivalence relation. Members of one of its equivalence classes are "three trees," "three mountain peaks," "three birds," etc., giving rise to the number "3"; each equivalence class corresponds to a natural number. Colors arise from the relation among objetcs of having the same color, although, as usual in practical concept forming, there are bordeline (hard to classify) cases.

8.80 PROOF of the Fundamental Theorem of Equivalence Relations. For $a\in A$ let $[a]=\{b\in A\mid a\sim b\}$. We refer to this as the "candidate equivalence class of $A$." We need to prove that the candidate equivalence classes partition $A$ and that $\sim$ corresponds to that partition. The proof goes through a series of observations.
8.80(a)   $a\in [a]$ (by reflexivity)
8.80(b)   If $a\in [b]$ then $[a]\subseteq [b]$ (by transitivity)
8.80(c)   If $a\in[b]$ then $b\in [a]$ (by symmetry)
8.80(d)   If $b\in[a]$ then $[a]=[b]$ (from (b) and (c))
8.80(e)   $[a]$ and $[b]$ are either disjoint or equal (from (d))
8.80(f)   $\bigcup_{a\in A} [a] = A$ (from (a)).

8.82 DO   Prove 8.80(a)--(d).

8.84 HW (5 points, due Mon, Nov 2) Prove 8.80(e). Use 8.80 (a)--(d).

8.86 COMMENT: role of equivalence relations in concept formation. What the toddler recognizes in Example 8.45 is not the color of each bear but the equivalence relation of being of the same color. This equivalence relation creates the partition that represents the concept of "color." Concept formation being the key function of intelligence, arguably, the Fundametal Theorem of Equivalence Relations could be called the Fundamental Theorem of Intelligence.

8.88 DEF   Given an equivalence relation $\sim$ on the set $A$, a system of representatives is a set $C\subseteq A$ such that $C$ contains exactly one element of each equivalence class. in particular, $|C|=$ the number of equivalence classes.

8.90 DEF (residue classes)  We have seen that for fixed $m$, the relation $a\equiv b \pmod m$ (congruence modulo $m$) is an equivalence relation among the integers. The equivalence classes of this relation are called the modulo $m$ residue classes.

8.92 DEF A system of representatives of the modulo $m$ residue classes is called a complete set of residues modulo $m$.

8.94 DO   The mod 5 residue classes are $5\zzz$, $5\zzz+1$, $5\zzz+2$, $5\zzz+3$, $5\zzz+4$.

8.96 DO   Let $m\ge 1$ and let $r_1,\dots,r_m$ be a complete set of residues mod $m$. Then the residue classes are $m\zzz+r_1$, $m\zzz+r_2$, $\dots$, $m\zzz+r_m$.

8.98 HW (3 points, due Mon, Nov 2)   What are the residue classes modulo $0$? State the size of each residue class and describe, using the set notation, the set of residue classes. Make sure you properly use the braces.

8.100 DO   Prove: if $m\neq 0$ then the number of mod $m$ residue classes is $|m|$.

8.102 HW (4 points, due Mon, Nov 2)     Let $m\ge 1$. Prove: the integers $r_1,\dots,r_m$ form a complete set of residues modulo $m$ if and only if they are pairwise not congruent modulo $m$, i.e., $(\forall i,j)((r_i\equiv r_j \pmod m)\Leftrightarrow (i=j))$.

8.104 HW (5 points, due Mon, Nov 2)   Let $m\ge 1$ and let $r_1,\dots,r_m$ be a complete set of residues modulo $m$. Prove: $(\forall c\in\zzz)(cr_1,\dots,cr_m$ form a complete set of residues modulo $m \Leftrightarrow \gcd(c,m)=1)$.

Class 7, Tue 10-20   HW and Bonus problems due Monday, October 26, except where otherwise stated. The following items from Class 6 are also due Monday, October 26:   HW 6.24, 6.26, 6.35, 6.56 and Bonus 6.28, 6.44, 6.58.
WARNING. Some of the problems have been updated; they are marked to indicate this.

7.10 Theorem (Euclid, cca. 350 BCE)   There are infinitely many prime numbers.
Formally:   $(\forall n)(\exists p)((p > n) \wedge ( p$ is a prime$))$, meaning that for every number $n$ there is a prime number that is greater. This is the way it was stated by the ancient Greeks; the notion of an "infinite set" is modern, it only arose in the 19th century, largely from the work of Georg Cantor.

7.11 NOTATION   "BCE" stands for "Before the Common Era." Its meaning is the same as "BC" but it avoids the explicit reference to the doctrine of a particular religion. The similarly neutral counterpart of "AD" is "CE", meaning "Common Era."

7.13 Proof of the infinitude of primes.   We prove the formal statement $(\forall n)(\exists p)((p > n) \wedge ( p$ is a prime$))$. So our input is an integer $n$ and we need to find a prime that is greater than $n$.
Let $P=\prod_{p\le n} p$ be the product of all primes $p\le n$. So $P\ge 1$. (Why?) Let $q$ be a prime divisor of $P+1$. (Such $q$ exists because $P+1\ge 2$.)
Claim.   $q > n$.
So this claim provides the desired prime, and completes the proof.   QED

7.15 HW (4 points)   Prove the Claim stated in 7.13. Use the language of congruences.

7.17 DO   Prove that there are infinitely many primes $p$ such that $p\equiv -1 \pmod{4}$.

7.19 Bonus (5 points, due Mon Nov 2)   Prove that there are infinitely many primes $p$ such that $p\equiv -1 \pmod{6}$.

7.21 THEOREM   There are infinitely many primes $p\equiv 1\pmod 6$ and also infinitely many primes $p\equiv 1\pmod 4$. These results are more difficult to prove, but the proof is still elementary and could be explained in class (if we had time). Both of these are subsumed by the theorem that there are infinitely many primes $p\equiv 1\pmod{12}$. In fact, a far more general result was found more than 180 years ago (see below).

7.23 DO   If $\gcd(a,m) > 1$ then there is at most one prime number $p\equiv a \pmod m$.

7.25 Theorem (primes in arithmetic progressions, Dirichlet, 1837)   If $a$ and $m$ are relatively prime and $m\neq 0$ then there are infinitely many primes $p\equiv a \pmod m$.

Example:   There are infinitely many primes $p\equiv 77 \pmod{120}$.

The proof of this amazing theorem is based on a surprising connection between number theory and the theory of complex functions.

7.26 DO   Why do we call this theorem "primes in arithmetic progressions"?

7.30 DO (Cancellation Law for congruences) If $\gcd(c,m)=1$ then $(\forall a,b)((ac\equiv bc\pmod m)\Leftrightarrow (a\equiv b\pmod m))$.
(The $\Rightarrow$ part was HW 6.100.)

7.32 DO (Generalized cancellation Law for congruences Let $\gcd(c,m)=d$. Then $(\forall a,b)(ca\equiv cb \pmod m \Leftrightarrow a\equiv b \pmod{m/d})$

7.35 (Fermat's little Theorem (FlT)) If $p$ is a prime then $(\forall x)(x^p\equiv x\pmod p)$.

7.37 COMMENTS   This lovely theorem, that has been a delight of scholars of pure mathematics for centuries, has in the past few decades become "applied mathematics" -- becoming one of the indispensable foundations of a trillion-dollar industry, namely, e-commerce. Specifically, FlT has for decades been the basis of Public Key Cryptography. Each time you transmit your encrypted credit card number to a vendor over the internet, you are relying on Fermat's little Theorem. A little theorem well worth proving!

7.40 Let us prove FlT for $p=2$. We need to show:   $(\forall x)(2\mid x^2-x)$.   Proof:   $x^2-x=x(x-1)$ is the product of two consecutive integers. One of those is even.   QED

7.42 Let us prove FlT for $p=3$. We need to show:   $(\forall x)(3\mid x^3-x)$.   Proof:   $x^3-x=x(x^2-1)=x(x-1)(x+1)=(x-1)x(x+1)$ is the product of three consecutive integers. One of those is divisible by 3.   QED

7.44 Let us prove FlT for $p=5$. We need to show:   $(\forall x)(5\mid x^5-x)$.   Proof:   $x^5-x=x(x^4-1)=x(x^2-1)(x^2+1)=(x-1)x(x+1)(x^2+1)$. Now observe that $x^2+1\equiv x^2-4 \pmod 5$ and $x^2-4=(x-2)(x+2)$, so $x^5-x\equiv (x-2)(x-1)x(x+1)(x+2) \pmod 5$. But the RHS (right-hand side) is a product of 5 consecutive integers, so it is $0 \pmod 5$.   QED

7.46 Bonus (4 points) Prove FlT for $p=7$ by showing that $x^7-x\equiv (x-3)(x-2)(x-1)x(x+1)(x+2)(x+3) \pmod 7$, strengthening the ideas of the proof for $p=5$. Use the identities $x^3-1=(x-1)(x^2+x+1)$ and $x^3+1=(x+1)(x^2-x+1)$. Give a very simple proof of the congruence $(x^2+x+1)(x^2-x+1)\equiv (x-3)(x-2)(x+2)(x+3) \pmod{7}$. Simplicity counts.
Note that these congruences (for each concrete value of $p$) could also be proved by simply plugging in all values of $x$ from $0$ to $p-1$, or better yet, from $-(p-1)/2$ to $(p-1)/2$. Proofs that use this technique will not be accepted.

7.48 COMMENT   These proofs get increasingly complicated as $p$ grows. A general proof that works for all $p$ will come soon.

7.50 Fermat's little Theorem, version 2   Let $p$ be a prime number. Then $(\forall x)((p\nmid x) \Rightarrow (x^{p-1}\equiv 1 \pmod p))$

7.52 HW (6 points, due Mon, Nov 2)   Prove that the two versions of FlT (7.35 and 7.50) are equivalent.
Warning: this is an "if and only if" statement. For each direction, clearly state what is the assumption and what is the desired conclusion.

7.54 HW (6 points)   Evaluate $(5^{9,000,000} \bmod{37})$.
(See Notation 6.54; in particular, your answer should be an integer between $0$ and $36$.)
Do NOT do any calculation, just use FlT and basic facts about divisibility and congruences. Clearly state your answer. Show all your work.
(WARNING: this problem was updated 10-23 3:30am.)

7.60 DEF   Let $L\subseteq \zzz$. We say that $L$ is closed under addition if $(\forall a,b)((a\in L)\wedge(b\in L)\Rightarrow(a+b\in L))$.   Closure under subtraction is defined analogously:   We say that $L$ is closed under subtraction if $(\forall a,b)((a\in L)\wedge(b\in L)\Rightarrow(a-b\in L))$.

7.62 DO   $\nnn$ (the set of positive integers) is closed under addition but it is not closed under subtraction. (Why?) The same holds for $\nnn_0$, the set of non-negative integers. (Why?)

7.64 HW (3 points)   Is the empty set closed under addition? Under subtraction? Prove your answers.

7.66 HW (4 points)   Find all finite subsets $A\subseteq\zzz$ that are closed under addition. Clearly state your answer. Prove.

7.68 DEF   Recall DEF 2.32: For $A\subseteq \zzz$ and $k\in\zzz$ we let $kA:=\{ka\mid a\in A\}$.

7.70 DEF   Recall DEF 2.16 (sumset): For $A, B\subseteq\zzz$ we let $A+B:=\{a+b\mid a\in A, b\in B\}$. More generally, for any finite index set $I$ (possibly empty) and sets $B_i\subseteq \zzz$ for $i\in I$ we define $\sum_{i\in I} B_i = \{\sum_{i\in I} b_i \mid b_i\in B_i\}$.
Example.   $A+B+C=\{a+b+c\mid a\in A, b\in B, c\in C\}$.

7.71 HW (4 points) Let $B_i\subseteq\zzz$. What is $\sum_{i\in\emptyset} B_i$ ? Give a clear answer. Prove.

7.72 DO   Observe that $a\zzz+b\zzz=\{ax+by\mid x,y\in\zzz\}$ is the set of all linear combinations of $a$ and $b$.

7.74 HW (4 points)   Interpret $a\zzz+b\zzz+c\zzz$:   write it using the setmaker bar notation and also describe it in words, as in the preceding exercise. Your interpretation should be based on DEF 7.70. No proof required.

7.76 DO   If $k\in \nnn$ then $k\nnn$ is closed under addition.

7.78 HW (3 points) Find a non-empty subset $A\subseteq \nnn$ that is closed under addition but cannot be written as $A=k\nnn$. Give a clear definition of $A$. No proof required.

7.80 HW (2 points) Prove: If $A,B\subseteq \zzz$ are closed under addition then their sumset $A+B$ is also closed under addition.

7.90 HW (4 points) Prove:   If $A\subseteq\zzz$ is closed under subtraction then $A$ is also closed under addition. (You can use without proof exercises above but not below in this section.)

7.92 HW (4 points) Let $A,B\subseteq\nnn$ be non-empty sets, closed under addition. Prove: $A\cap B\neq\emptyset$.

7.94 HW (3 points) Let $I$ be a (finite or infinite, possibly empty) index set and let $B_i\subseteq\zzz$ be closed under addition. Prove: $\bigcap_{i\in I} B_i$ is closed under addition.

7.96 DO   Same as the preceding exercise, just replace "addition" by "subtraction."

7.100 DEF (module)   Let $M\subseteq \zzz$. We say that $M$ is a module if (1) $M\neq \emptyset$ and (2) $M$ is closed under subtraction.

7.102 DO   If $M$ is a module then $0\in M$.
Proof. Let $a\in M$. (How do we know such $a$ exists?) Then $a-a\in M$.   QED

7.104 EXAMPLES   $\zzz$ and $\{0\}$ are modules. The set of even numbers, $2\zzz$, is a module. (The set of odd numbers is NOT a module! Why?) More generally, for any $k\in\zzz$, the set $k\zzz$ is a module. (DO: verify!)

7.106 DO   If $M$ is a module and $a\in M$ then $-a\in M$.
Proof. Since $0\in M$ and $a\in M$, we have $-a=0-a\in M$.   QED

7.108 DO   If $M$ is a module then $M$ is closed under addition.
Proof. Let $a,b\in M$. Then $a+b=a-(-b)\in M$.   QED

7.110 HW (5 points) Prove: If $M$ is a module and $k\in M$ then $k\zzz\subseteq M$.
You may use the exercises above without proof, but if you use them, you need to reference them. Use induction, not imprecise "we can continue in the same manner"-type arguments. Give a clear statement of what it is that you are proving by induction.

7.111 DO   Prove: If $A, B\subseteq\zzz$ are modules then $A\cap B$ is a module. More generally, if $I$ is a (finite or infinite, possibly empty) index set and $B_i\subseteq\zzz$ is a module for $i\in I$ then $\bigcap_{i\in I} B_i$ is a module.

7.112 DO   Prove: If $A, B\subseteq\zzz$ are modules then their sumset $A+B$ is a module. More generally, if $I$ is a finite index set (possibly empty) and $B_i\subseteq\zzz$ are modules for $i\in I$ then $\sum_{i\in I} B_i$ is a module.

7.115 DO (Division Theorem) Let $a,b\in\zzz$ where $b\neq 0$. Then there exist $q,r\in\zzz$ such that
    (a)   $a=bq+r$ and
    (b)   $0\le r < |b|$
Examples.   (1)   $a=73, b=15$:   $73=15\cdot 4+13$;    (2)   $a=-73, b=15$:   $-73=15\cdot (-5)+2$.
Hint. Fix $b$. First prove this for $a\ge 0$ by induction on $a$. Then prove it for negative $a$ using that we already have the result for $-a$.
We call $q$ the integer quotient and $r$ the least non-negative remainder.
We shall see how to accelerate Euclid's algorithm using the Division Theorem.

7.120 DEF   A cyclic module is a module of the form $k\zzz$ for some $k\in\zzz$. (Recall: this is the set of all multiples of $k$.) For instance $\zzz$ itself is a cyclic module $(k=1)$, the zero module $\{0\}$ is also cyclic $(k=0)$, the set of even numbers is a cyclic module $(k=2)$.

7.122 Bonus (structure theorem for modules, 6 points, due Mon Nov 2) Prove that every module is cyclic.
In other words, if $M$ is a module then $(\exists k)(M=k\zzz)$. You may use the exercises above without proof.
Hint. We need to find $k$ such that $M=k\zzz$. Give a simple definition of a suspect (a value $k$ that you believe satisfies $M=k\zzz$). You need to show two things: (a) $k\zzz\subseteq M$ and (b) $M\subseteq k\zzz$. Clearly separate the proofs of these two statements; make it clear in each part, what is the assumption and what is the desired conclusion. For part (b), use the Division Theorem.

7.124 HW (2+2 points) Let $a,b\in\zzz$ and $M=a\zzz+b\zzz$. Prove: (a) $a,b\in M$   (b) $M$ is a module. You may use the exercises above without proof.

7.126 HW (4 points) Prove: If $d$ is a common divisor of $a$ and $b$ and $d$ can be written as a linear combination of $a$ and $b$ then $d$ is a greatest common divisor of $a$ and $b$. (First review the definition of a greatest common divisor, 5.80 DEF.)

7.128 HW (6 points) Let $a,b\in\zzz$. Use the preceding three exercises to give a strikingly elegant alternative proof of the fact that a greatest common divisor of $a$ and $b$ exists and it can be written as a linear combination of $a$ and $b$ (Bézout's Lemma).
Your proof cannot assume the existence of a greatest common divisor. Review the definition of a greatest common divisor (5.80 DEF).

7.130 DO Let $a,b,c$ be integers. (a) Define what it means that the integer $d$ is a greatest common divisor of $a,b,c$. Model your definition after Def. 3.4. (b) Prove that such $d$ exists. (c) Prove that $d$ is a linear combination of $a,b,c$, i.e., $d$ can be written in the form $d=ax+by+cz$ (Bézout's Lemma). Model your proof of (b) and (c) after the preceding exercise. The entire proof should take no more than a few lines.

7.135 Bonus (existence of lcm, 6 points, due Mon Nov 2) Use the structure theorem for modules (7.122) to prove that $(\forall a,b\in\zzz)$ there exists a least common multiple (DEF 5.82). You may use any exercise above without proof. Do not use the Fundamental Theorem of Arithmetic.
Hint. What is the set of multiples of $a$? and of $b$? Use these to describe the set of common multiples of $a$ and $b$. Use the structure theorem to find a suspect, and prove the suspect guilty as charged in DEF 5.82.

7.140 DEF   (infinite sum) Let $I$ be an infinite index set and let $B_i\subseteq \zzz$ be sets such that $(\forall i\in I)(0\in B_i)$. Then we define $\sum_{i\in I}B_i$ as the set all finite sums of the form $\sum_{i\in J} b_i$ where $b_i\in B_i$ and $J\subseteq I$ is finite. In other words, $$\sum_{i\in I}B_i= \bigcup_{J\subseteq I, J\text{ finite}} \sum_{i\in J}B_i$$ The reson we insist on $0\in B_i$ is that we think of the finite sums as infinite sums where all terms outside the finite set $J$ are zero.

7.142 DO   Prove: If $I$ is a finite or infinite index set and $B_i\subseteq \zzz$ is a module for each $i\in I$ then $\sum_{i\in I} B_i$ is a module.

7.144 DO   Let $S\subseteq\zzz$ be a (finite or infinite, possibly empty) subset. Define what it means that $d\in\zzz$ is a greatest common divisor of $S$.

7.146 DO   Use the structure theorem and exercise 7.142 to prove that every subset of $\zzz$ has a greatest common divisor.

7.148 DO   Use the structure theorem to prove that every subset of $\zzz$ has a least common multiple.

7.150 HW (5 points) Find the gcd of the set $S:=\{p^2-1 \mid p\text{ is a prime and }p\ge 30\}$. Your solution needs to include your answer to DO 7.144 (the definition of the gcd of a set of numbers). Prove your answer based on this definition.
WARNING.   This problem was updated 10-23 3:20am.

Class 6, Thu 10-15   Union, intersection symbols, well-ordering principle and proof by induction, prime property and proof of the Fundamental Theorem of Arithmetic

6.01 HW (2 points) Your geographic location during this term:   Hyde Park, or elsewhere in Chicago, or if not in Chicago: Country/State or province, City or metropolitan area, time zone.

6.10 HW (4+2+2)   (a)   Let $A$ and $\Omega$ be sets and let $f:A\to\calP(\Omega)$ be a function. So for every $i\in A$, the value $f(i)$ is a subset of $\Omega$. Let us write $B_i := f(i)$. For a subset $I\subseteq A$, define the union $$ \bigcup_{i\in I} B_i\,.$$

Model the meaning of this expression after the meaning of the summation symbol. It should work for all subsets $I\subseteq A$, including the empty set. A set $C\subseteq\Omega$ is defined if for all objects $x$ in the given universe, we can decide whether $x\in C$. Therefore your definition should be of the following form: $$ (\forall x\in\Omega)\left(x\in\bigcup_{i\in I} B_i\Leftrightarrow \text{ (a statement about }x\text{ and }I)\right)\,.$$ Your job is to find the statement about $x$ and $I$. Make sure to use the proper quantifiers.

(b) I am not asking you to prove this statement for a very simple reason. What is the reason?

(c) Determine   $\bigcup_{i\in\emptyset} B_i$. Your answer should be very simple.

6.12 HW (3+3)   (a)   Let $A$ and $\Omega$ be sets and let $f:A\to\calP(\Omega)$ be a function. Let $B_i :=f(i)$. Following the example of the preceding exercise, do the analogous job for intersections. So you need to find a definition of the form $$ (\forall x\in\Omega)\left(x\in\bigcap_{i\in I} B_i\Leftrightarrow \text{ (a statement about }x\text{ and }I)\right)\,.$$ Again, your job is to find the statement about $x$ and $I$. Make sure to use the proper quantifiers.

There is no part (b) to this exercise.

(c) Determine   $\bigcap_{i\in\emptyset} B_i$. Your answer should be very simple.

6.14 DO   Prove the distributive laws: if $B_i\subseteq\Omega$ and $C\subseteq\Omega$ then $$ C\cap \left( \bigcup_{i\in I} B_i\right) = \bigcup_{i\in I} (C\cap B_i) $$ and $$ C\cup \left(\bigcap_{i\in I} B_i\right) = \bigcap_{i\in I} (C\cup B_i) $$

6.16 DO   State and prove De Morgan's laws in the context of the notation introduced in the preceding exercises.

6.20 DO   Study the last few slides of the October 8 class. These slides were discussed in the October 15 class. They show a fragment of the divisibility hierarchy of positive integers. In this diagram, the nodes are the positive integers (so there are infinitely any nodes), and the links correspond to immediate divisors, i.e., there is a link $a\to b$ if $b/a$ is a prime number. Such a diagram (nodes and links) is called a directed graph or digraph, for short. A path from node $x$ to node $y$ is a sequence of links we can follow to get from $x$ to $y$. Examples: $1 \to 3 \to 6 \to 30$ is a path of length 3 (3 steps) form $1$ to $30$. Another path of length 3 from $1$ to $30$ is $1\to 5 \to 10\to 30$. The slides show two highlighted paths.

6.22 DO   Prove: for $a,b\in\nnn$, an $a\to\dots\to b$ path exists in the divisibility hierarchy if and only if $a\mid b$.

6.24 HW (6+4, due Monday, October 26) (a)   For $n\in \nnn$, count the paths from $n$ to $4310n$ in the divisibility hierarchy. Briefly reason your answer.    (b)   State a more general result of this type. It should be very simple to state, and the answer should be a closed-form expression, permitting the use the factorial function. Briefly reason your answer.

6.26 HW (5 points, due Monday, October 26) Characterize those pairs $(a,b)$ of positive integers for which there is a unique $a\to\dots\to b$ path. (Recall that characterization means an "if and only if" condition.) Briefly reason your answer.

6.28 Bonus (6 points, due Monday, October 26) Let $n=3^k\cdot 7^{\ell}$ where $k,\ell \ge 0$. Count the paths from $1$ to $n$ in the divisibility diagram. Your answer should be a simple closed-form expression in terms of $k$ amd $\ell$ (allowing the factorial function). Prove your answer.

6.35 HW (5 points, due Monday, October 26)   Prove by induction:   $(\forall n\ge 1)(|F_n^2 - F_{n-1}F_{n+1}|=1)$.

6.38 DEF   We say that the infinite sequence $a_0, a_1, a_2, \dots$ is periodic with period $m\ge 1$ if $(\forall i,j)(i\equiv j \pmod m \Rightarrow a_i=a_j)$.
(CORRECTION: The condition that $m\ge 1$ was added 10-22 at 2:30am.)
Example: the sequence $1,2,-5,1,2,-5,1,2,-5,\dots$ is periodic with period 3. It is also periodic with period 6.  

6.40 DO   If a sequence is periodic with period $m$ and $m\mid n$ then the sequence is also periodic with period $n$. From what property of divisibility does this follow?

6.42 DO   $(-1)^n$ is periodic with period $2$.

6.44 Bonus (6 points, due Monday, October 26)   Prove: If a sequence is periodic with period $k$ and also with period $\ell$ then it is periodic with period $\gcd(k,\ell)$.

6.46 DEF   a geometric progression is a sequence of complex numbers of the form $a, aq, aq^2, aq^3,\dots$. The number $q$ is the quotient of the geometric progression.

6.48 HW (4 points) Prove: If a geometric progression of real numbers is periodic then it is periodic with period 2.

6.50 Bonus (3 points) Find a geometric progression that is periodic with smallest period $3$.

6.52 HW (5 points) Find all geometric progressions $a_0, a_1, \dots$ that start with $a_0=1$ and satisfy the Fibonacci recurrence $a_n = a_{n-1}+a_{n-2}$ $(n\ge 2)$. How many such geometric progressions are there? State their quotients.

6.54 NOTATION   For $m\neq 0$ we write $(a \bmod m)$ to denote the least non-negative integer $r$ such that $r\equiv a\pmod m$. In particular, $0\le (a \bmod m) \le |m|-1$.
Examples:   $(37 \bmod{17})=3$,    $(37 \bmod{-17})=3$,    $(-37 \bmod{17})=14$,    $(34 \bmod{17})=0$.

6.56 HW (5 points, due Monday, October 26) Let $m=3$. Consider the sequence $b_n= (F_n \bmod 3)$.
   (a)   Write down the members of this sequence from $n=0$ to $12$.
   (b)   Prove that this sequence is periodic and determine its smallest period.

6.58 Bonus (8 points, due Monday, October 26)   Let $m \ge 2$. Let $b_k=(F_k \bmod m)$. Prove: the sequence $b_k$ is periodic with period $\le m^2-1$.
[Updated 10-28. Original erroneously assumed $m\neq 0$ only. The statement is false for $m=1$.]

6.62 WELL-ORDERING PRINCIPLE.   Every non-empty subset of the natural numbers has a least element.
Notation. If $A\subseteq \nnn$ and $A\neq\emptyset$, we denote the least element of $A$ by $\min A$. Example: $\min\{9,7,13\} = 7$. (Recall the notation $\nnn=\{1,2,3,\dots\}$ denotes the set of natural numbers. But everything we say below also works for $\nnn_0=\{0,1,2,\dots\}$ -- the set of non-negative integers, because the well-ording principle is valid for $\nnn_0$ as well.)

This principle is the basis of proof by induction.

6.64 DO (Induction principle)   Let $A\subseteq\nnn$ be a subset and for $n\in\nnn$ let $P_n(A)$ denote the following condition: $(\forall j\in \nnn)(j < n \Rightarrow j\in A)$. (We call $P_n(A)$ the $n$-th Inductive Hypothesis.)
Let $Q_n(A)$ be the statement that "$P_n(A)\Rightarrow (n\in A)$". (We call $Q_n(A)$ the $n$-th inductive step.)
Suppose $(\forall n\in\nnn)(Q_n(A)$ is true$)$. Then $A=\nnn$.
Proof by contradiction. Suppose $A\neq \nnn$. Let $B=\nnn\setminus A$. Then $B\neq\emptyset$. Let $n=\min B$.   (This $n$ exists by the Well-Ordering Principle.) Since $n$ is the least element of $B$, $P_n(A)$ is true. Then, by the $n$-th inductive step, $n\in A$. So $n\in A\cap B$, contradicting our definition of $B$.    Q.E.D.

6.65 HW (4 points)   Prove: $P_1(A)$ is automatically true for every set $A$. (No "base case" was needed for the Induction principle.)    [Typo in problem fixed 10-16 1:13pm.]

6.66 The principle of "Proof by induction." We have a sequence of statements, $S(1), S(2),\dots$ (a statement $S(n)$ for every $n\in \nnn$). Our goal is to prove that $(\forall n)(S(n)$ is true$)$.
Let $A$ denote the set of those values $n\in\nnn$ for which $S(n)$ is true. So we want to show that $A=\nnn$. By the Induction Principle, if we can prove the $n$-th inductive step for every $n$, then we shall have proven that $A=\nnn$.

6.67 EXPLANATION. We have seen that there is no need for a base case. Why do we then talk about a base case, or sometimes even of infinitely many base cases, as in the proof of existence the $\gcd(a,b)$ where all cases where $a=0$ or $b=0$ counted as "base cases"? These are cases that require separate treatment because our way of treating the inductive step in the "general case" (in the example: when $a,b\neq 0$) does not work for them. It would be more proper to call them boundary cases.

6.70 DO   Prove: every natural number $n\in \nnn$ can be written as a product of primes.   (Note: the number $n=1$ is no exception: it is the empty product of primes.)   Proof by induction.

6.72 DEF   We say that a number $n\in\zzz$ has the prime property if   (a)   $n\neq \pm1$, and   (b)   $(\forall a,b\in\zzz)((n\mid ab) \Rightarrow (n\mid a)\vee(n\mid b))$.

6.73 DO   If $n$ has the prime property then $-n$ also has the prime property.

6.75 DEF &nnbsp; A number $p$ is a prime number if $p\ge 2$ and $p$ has exactly 2 positiove divisors: $1$ and $p$.

6.76 DO   If $p$ is a prime number then $(\forall a)(\gcd(a,p)\in\{1,p\})$.

6.78 DEF   A number $n\in\zzz$ is composite if $(\exists a,b)(|a| <|n|$ and $|b| < |n|$ and $n=ab)$.

6.80 DO   Let $n\in\zzz$. Then either $n=0$ or $n=\pm 1$ or $n$ is a prime number or $-n$ is a prime number or $n$ is a composite number.

6.82 DO   Prove: If $n$ is a composite number then $n$ does not have the prime property.

6.84 HW (4 points)   Does $0$ have the prime property? Prove your answer.

6.86 Prime Property Theorem.  All prime numbers have the prime property.
This is a nontrivial result. It contains the essence of the Fundamental Theorem of Arithmetic. It can be found in Euclid's Elements, cca. 350 BCE. We follow Euclid in basing the proof on Euclid's Lemma.

6.88 DO (Euclid's Lemma)   Prove:   $(\forall a,b)(\gcd(a,b)=\gcd(a-b,b))$.

6.90 DO (Bézout's Lemma) $(\forall a,b)(\exists x,y)( \gcd(a,b)=ax+by)$.   This was assigned last time. The proof goes by induction, using Euclid's Lemma.

6.92 Proof of the Prime Property Theorem (6.86)   Let $p$ be a prime number. Assume $p\mid ab$. We need to show that $p\mid a$ or $p\mid b$.
If $p\mid a$, we are done. Assume now $p\nmid a$. We need to show that $p\mid b$.
Since $p\nmid a$, we cannot have $\gcd(p,a)= p$, so we have $\gcd(p,a)=1$ (Exercise 6.77). Therefore, by Bézout's Lemma, $(\exists x,y)(ax+py=1)$. Multiplying this equation by $b$ we get $abx+pby=b$. Here $p\mid abx$ because $p\mid ab$, and $p\mid pby$ by the definition of divisibility, so $p\mid abx+pby=b$ (Proposition 1.44), therefore $p\mid b$.    Q.E.D.

6.93 Comment.   "Q.E.D." stands for the Latin phrase "Quod erat demonstrandum," meaning "What was to be shown." It marks the end of a proof.

6.94   Let $p$ be a prime number and $a_1,\dots,a_k$ integers. Prove by induction on $k$: if $p\mid a_1\cdots a_k$ then $(\exists i)(p\mid a_i)$.

6.96 DO   Use Theorem 6.86 to prove the uniqueness of prime factorization (Fundamental Theorem of Arithmetic). Here uniqueness means uniqueness up to ordering. In other words, if $p_1,\dots,p_k$ are not necessarily distinct prime numbers and $q_1,\dots, q_{\ell}$ are also not necessarily distinct prime numbers, and $p_1 \cdots p_k = q_1\cdots q_{\ell}$ then $k=\ell$ and there exists a bijection $f:[k]\to[\ell]$ such that $(\forall i)(p_i=q_{f(i)})$. Proof by induction on $k$. Make $k=0$ your base case.

HW 6.98 (5 points)   Prove:   $(\forall a,b,m)($ if $m\mid ab$ and $\gcd(a,m)=1)$ then $m\mid b$. Do not use the Fundamental Theorem of Arithmetic. Instead, follow the idea of the proof of Theorem 6.86.

HW 6.100 (Cancellation law for congruences, 4 points)   Prove: If $ac\equiv bc \pmod m$ and $\gcd(c,m)=1$ then $a\equiv b \pmod m$. The proof should be one line with reference to a previous HW problem.

Class 5, Tue 10-13   Summation, product symbols, arithmetic functions, multiplicativity, least common multiple

5.10 DEF   Let $f:A\to \rrr$. The expression $$\sum_{x\in A} f(x)$$ means the sum of all values of $f(x)$ for $x\in A$. Inline it looks like this:   $\sum_{x\in A} f(x)$

5.12 Special case: $f$ is the constant function $(\forall x)(f(x)=1)$:   counting:  $\sum_{x\in A} 1 = |A|$.

5.14 Example.   Let $f(x)=x^2$,  $A=\{-3,2,7\}$. Then $\sum_{x\in A} x^2 = (-3)^2 + 2^2 + 7^2 = 9 + 4 + 49 = 62$.

5.16 NOTATION.   If $A=[n]$ then we have the classical notation $$ \sum_{i\in [n]} f(i) = \sum_{i=1}^n f(i). $$

5.18 DO   $\sum_{i=1}^n i = n(n+1)/2$.   Prove by induction.

5.20 DO   $\sum_{i=1}^n i^2 = n(n+1)(2n+1)/6$.   Prove by induction.

5.22 DO   Prove by induction: $$\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2\,.$$

5.23 COMMENT   Notice that this means the amusing fact that $\sum_{i=1}^n i^3 = \left(\sum_{i=1}^n i\right)^2$.

5.24 HW (5 points) Evaluate this sum: $$\sum_{i=1}^n \frac{1}{i(i+1)} $$ Your answer should be a simple closed-form expression in terms of $n$. Experiment, guess the expression, and prove it by induction.

5.25 HW (5 points) Consider the sum $$ K(n) :=\sum_{1\le i \le j \le n} f(i,j) $$ This means the summation is over the set of pairs $(i,j)$ that satisfy the constraint $1\le i\le j\le n$. Examples: $K(1)=f(1,1)$,   $K(2)=f(1,1)+f(1,2)+f(2,2)$, $K(3)=f(1,1)+f(1,2)+f(1,3)+f(2,2)+f(2,3)+f(3,3)$.
What is the number of terms in this sum? Your answer should be a simple closed-form expression. Reason your answer.

5.26 Bonus (5 points) Evaluate the sum $$ \sum_{1\le i \le j \le n} j $$ You may use without proof results stated in exercises above in this section.

5.27 DEF What does this sum mean? $$\sum_{A\subseteq [n]} f(A)$$ It means we are summing over all subsets of $[n]$, so it is the same as $\sum_{A\in\calP([n])} f(A)$ (for some function $f$ of which the domain is the powerset $\calP([n])$).

5.28 DO   $\sum_{A\subseteq [n]} 1 = 2^n$

5.29 HW (5 points)   Evaluate the sum $$\sum_{A\subseteq [n]} (-1)^{|A|}$$ Find a very simple answer (for every $n\ge 0$). Prove your answer.

5.30 Bonus (6 points)   Evaluate the sum $\sum_{A\subseteq [n]} |A|$. Give a simple closed-form expression (no summation sign or dot-dot-dot). Prove your answer.

5.33 DEF Let $\nnn=\{1,2,3,\dots\}$ denote the set of natural numbers. The quantity $d(n)$ is defined as the number of positive divisors of $n\in\nnn$. Examples: $d(1)=1$, $d(2)=2$, $d(3)=2$, $d(4)=3$, $d(5)=2$, $d(6)=4$, $d(7)=2$, $d(8)=4$. (Verify!)

5.35 DEF   $p$ is a prime if $d(p)=2$.

5.37 DO   Let $p$ be a prime and $k\ge 0$. Then $d(p^k)=k+1$.

5.39 DEF   An arithmetic function is a function $f:\nnn \to \ccc$.

5.41 DEF   An arithmetic function $f$ is multiplicative if the following statement is true:
$$(\forall k,\ell\in\nnn)(\gcd(k,\ell)=1 \Rightarrow f(k\ell)=f(k)f(\ell))$$

5.43 DO   Prove:   The $d(n)$ function is multiplicative.   Use the Fundamental Theorem of Arithmetic (uniqueness of prime factorization).

5.45 DEF   The product symbol is defined analogously to the summation symbol: $$\prod_{x\in A} f(x)$$ means the product of all values of $f(x)$ for $x\in A$.

5.47 DO   Let $n=p_1^{k_1}\cdots p_t^{k_t}=\prod_{i=1}^t p_i^{k_i}$ be the factorization of $n$ into powers of distinct primes. Then $$d(n)=\prod_{i=1}^t (k_i+1).$$

5.49 DO   Use the preceding exercise to prove that $(\forall n)(d(n)$ is odd $\Leftrightarrow$ $n$ is a square$)$.   (Note: this is not the simplest or most elegant proof of this result. It only serves as an illustration of how one can apply the preceding result.)

5.52 DEF Euler's phi function $\vf(n)$ is defined as the number of those $k\in [n]$ that are relatively prime to $n$.   Examples: $\vf(1)=1$, $\vf(2)=1$, $\vf(3)=2$, $\vf(4)=2$, $\vf(5)=4$, $\vf(6)=2$, $\vf(7)=6$, $\vf(8)=4$. (Verify!)

5.54 DO   Prove:   If $p$ is a prime number then $\vf(p)=p-1$.

5.56 DO   Let $p$ be a prime and $r\ge 1$. Then $(\forall k\in\zzz)(k$ is not relatively prime to $p^r$ if and only if $p\mid k)$

5.58 DO   Let $p$ be a prime and $r\ge 1$. Then $\vf(p^r)=p^r-p^{r-1}=p^r(1-1/p)$.

5.60 FACT (to be proved later)   The function $\vf$ is multiplicative.

5.62 DO   Let $n=\prod_{i=1}^t p_i^{k_i}$ be the factorization of $n$ into powers of distinct primes. Then $$\frac{\vf(n)}{n}=\prod_{p\mid n}\left(1-\frac{1}{p}\right)$$ Here the product extends over the distinct prime divisors of $n$.

5.63 Example.   If $n=3^k7^{\ell}$ where $k,\ell \ge 1$ then $\displaystyle{\frac{\vf(n)}{n} = (1-1/3)(1-1/7)=\frac{4}{7}}$ regardless of the exponents $k$ and $\ell$.

5.65 Bonus (6 points) Find the minimum value $\displaystyle{\min_{n\in [10000]}\frac{\vf(n)}{n}}$. Give your answer in the form of a fraction reduced to its smallest terms (numerator and denominator relatively prime). Prove your answer. Do not make any machine calculations. Show all your work. It should all fit on a half page.

5.67 Bonus (5 points)   $\sum_{d\ge 1, d\mid n} \vf(d) = n$.

5.70   What is the value of the empty sum $\sum_{x\in\emptyset} f(x)$?   This is a matter of convention, it does not follow from the definition of addition. But, reason that the only sensible value can be "zero." So, the empty sum is defined to have value $0.$

5.71   (a)   Let $f:\Omega\to \rrr$ be a function and let $A$ and $B$ be disjoint subsets of $\Omega$. Prove:  $\sum_{i\in A}f(i)+\sum_{i\in B}f(i)=\sum_{i\in A\cup B} f(i)$.
(b)   Show that part (a) would fail without the convention that $\sum_{i\in\emptyset} f(i)=0$.

5.72   What is the value of the empty product $\prod_{x\in\emptyset} f(x)$? Again, this is a matter of convention, but reason that the only sensible value can be "one."   So the empty product is defined to have value $1.$

5.73   (a)   Let $f:\Omega\to \rrr$ be a function and let $A$ and $B$ be disjoint subsets of $\Omega$. Prove:  $\prod_{i\in A}f(i)\cdot\prod_{i\in B}f(i)=\prod_{i\in A\cup B} f(i)$.
(b)   Show that part (a) would fail without the convention that $\prod_{i\in\emptyset} f(i)=1$.

5.74   Important examples of the empty product:
    $(\forall a\in\rrr)(a^0=1)$ (this includes the case $a=0$, so remember: $0^0=1$),   $0!=1$.

5.76 HW (5 points)   (a) Prove: $$\prod_{i=1}^n (1+x_i) = \sum_{A\subseteq [n]} \prod_{i\in A}x_i.$$ (b) What is the number of terms in the sum on the right-hand side? (Just state, do not prove.)   (c) Point out the role of the convention about the empty product in this identity.   (d) Based on this identity, expand the product $(1+x)(1+y)(1+z)$. (No proof required.)

5.80   Recall the definition of a greatest common divisor:
We say that $d\in\zzz$ is a greatest common divisor of $a,b\in\zzz$ if (1) $d\mid a$ and $d\mid b$ ($d$ is a common divisor) and (2) $(\forall e)((e\mid a \wedge e\mid b)\Rightarrow e\mid d)$ ($d$ is a common multiple of all common divisors).

5.82   Least common multiple. The definition is the dual of the definition of the greatest common divisors: we swap "divisor" and "multiple" everywhere in the definition.
DEF   We say that $m\in\zzz$ is a least common multiple of $a,b\in\zzz$ if (a) $a\mid m$ and $b\mid m$ ($m$ is a common multiple) and (b) $(\forall f)((a\mid f \wedge b\mid f)\Rightarrow m\mid f)$ ($m$ is a common divisor of all common multiples).

5.84 DO   If $m$ is a least common multiple of $a$ and $b$ then $-m$ is also a least common multiple of $a$ and $b$.

5.86 DO   If $m_1$ and $m_2$ are least common multiples of $a$ and $b$ then $m_2=\pm m_1$. We say that the least common multiple, if exists, is unique up to the sign.

5.88 NOTATION   If $m$ is a least common multiple of $a$ and $b$ then we write $\lcm(a,b)=|m|$. So, by definition, $\lcm(a,b)\ge 0$.

5.90 DO   $(\forall a)(\lcm(a,a)=|a|)$.

5.92 HW (5 points) Characterize those pairs $(a,b)\in\zzz\times\zzz$ for which $\lcm(a,b)=0$. (Characterization means a necessary and sufficient condition.) Your characterization should be a very simple condition. Prove your answer, based on the definition of lcm.

5.94 Note that we have not proved the existence of a least common multiple yet. We need to learn a little more about the gcd before proving that.

5.100 DEF   A linear combination of $a,b\in\zzz$ is a number of the form $ax+by$ for $x,y\in\zzz$.   Example: $5a-19b$ is a linear combination of $a$ and $b$.

5.102 DO   The set of all linear combinations of $a$ and $b$ is the set $a\zzz+b\zzz$.

5.104 DO   Prove: if $d\mid a$ and $d\mid b$ then $(\forall x,y\in\zzz)(d\mid ax+by)$. What property of elementary arithmetic are you using in the proof?

5.106 Bonus (Bézout's Lemma) (6 points)   Prove: $(\forall a,b\in\zzz)(\exists x,y\in\zzz)(\gcd(a,b)=ax+by)$ (the greatest common divisor can be written as a linear combination). Proceed by induction on $|a|+|b|$, following the steps of our proof that a greatest common divisor exists.

5.108 DO   Find $x,y\in\zzz$ such that $101x+61y=1$. Use Euclid's algorithm. Show your steps.

5.110 HW (6+3 points) Let $a=13x+6$ and $b=7x+5$ for some $x\in\zzz$.   (a) Prove:   $\gcd(a,b)=1$ or $23$.   (b) Find a value of $x$ such that $\gcd(a,b)=23$.
  Give a very simple proof of (a); simplicity counts. (There is a one-line proof.) For (b), just guess and verify.

Class 4, Thu 10-8   Greatest common divisor
HW and Bonus problems from this class and Class 3 are due Monday, October 12, 11:59pm, except where otherwise stated. Remember that Bonus problems 1.112 and 2.26 are also due at the same time.

4.08 TERMINOLOGY   Recall: If $d\mid n$, i.e., if $(\exists x)(dx=n)$, we say that $d$ is a divisor of $n$ and $n$ is a multiple of $d$.   Example: $8$ is a divisor of $56$ and $56$ is a multiple of $8$.

4.09 DO   Prove: (a) $a$ is both a divisor and a multiple of $a$. (b)   $a$ is both a divisor of $b$ and a multiple of $b$ if and only of $b=\pm a$.

4.10 DO   (a) $(\forall a)(0$ is a multiple of $a)$.   (b) $(\forall a)(a$ is a multiple of $1)$.   In other words, $0$ is on the top of the divisibility hierarchy and $1$ is at the bottom.

4.15 NOTATION   For $a\in \zzz$ we write $\Div(a)$ to denote the set of divisors of $a$. Example:   $\Div(14)=\{\pm1,\pm2,\pm7,\pm14\}$.
Note: This notation is only for use in this class, it is not a commonly used notation.

4.16 DO   $\Div(0)=\zzz$

4.17 DO   $\Div(a)=\Div(-a)$

4.18 DO   Prove: $a\mid b \ \Leftrightarrow\ \Div(a)\subseteq\Div(b)$. State, what property of divisibility is expressed by the $\Rightarrow$ direction of this statement. (Answer to the last question: transitivity. Work it out, why.)

4.20 DEF   We say that $d$ is a common divisor of $a$ and $b$ if $d\mid a$ and $\mid b$.

4.22 NOTATION   $\Div(a,b)=\Div(a)\cap\Div(b)$.

4.23 DO   $\Div(a,b)$ is the set of common divisors of $a$ and $b$.

4.25 DO   $\Div(a,b)=\Div(b,a)$.

4.26 DO   $\Div(a,b)=\Div(\pm a,\pm b)$.   (This statement is shorthand for the following statement:
$\Div(a,b)=\Div(-a,b)=\Div(a,-b)=\Div(-a,-b)$.

4.28 DO   $\Div(a,0)=\Div(a)$.

4.30 HW (6 points) (Euclid's Lemma) (modern rendering)   Prove:    $(\forall a,b)(\Div(a,b)=\Div(a-b,b))$.
Remember: to prove that two sets, $A$ and $B$, are equal, you have to show that they mutually contain each other: $A\subseteq B$ and $B\subseteq A$. Another way of looking at it: $A=B$ means $(\forall x)(x\in A \Leftrightarrow x\in B)$.

4.36 HW (4+4 points) True or false? Prove your answer.   (a)   $(\forall a,b)(\Div(a,a+b)\subseteq\Div(a,a+2b)$.   (b)   $(\forall a,b)(\Div(a,a+b)=\Div(a,a+2b)$.

4.37 Bonus (5 points) Find all values of $a$ such that the following statement holds:   $(\forall b)(\Div(a,a+b)=\Div(a,a+2b))$. Give a clear definition of the set of values $a$ for which you claim that the statement is true; prove.

4.40 REVIEW the definition of greatest common divisors and the proof of their existence via Euclid's Lemma from the slides. This is a substantial job, do not ignore.

4.70 DEF   The Fibonacci sequence $F_0,F_1,F_2,\dots$ is the sequence $0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,\dots$. The sequence is defined by the initial values $F_0=0, F_1=1$ and the recurrence $F_n=F_{n-1}+F_{n-2}$ $(n\ge 2)$. The members of this sequence are called Fibonacci numbers.

4.73 (4 points) HW   Prove: Consecutive Fibonacci number are relatively prime, i.e., $(\forall n\ge 0)(\gcd(F_n, F_{n+1})=1)$.

4.76 CH   Let $k,\ell \ge 0$. Prove: if $k\mid \ell$ then $F_k \mid F_{\ell}$.   Example: $F_5=5$ and $F_{10}=55$, so $F_5\mid F_{55}$.

4.78 CH   Let $k,\ell \ge 0$ and $d=\gcd(k,\ell)$. Prove: $\gcd(F_k, F_{\ell})=F_d$.

4.80 Bonus (6 points) Let $k,\ell \ge 0$ and $d=\gcd(k,\ell)$. Prove: $\gcd(2^k-1,2^{\ell}-1)=2^d-1$.

Class 3, Tue 10-6   Injections, surjections, Pigeon Hole Principle, Birthday paradox
HW and Bonus problems are due Monday, October 12, 11:59pm. Remember that Bonus problems 1.112 and 2.26 are also due at the same time.

3.0a DEF   An integer $p$ is a prime number if $p\ge 2$ and the only positive divisors of $p$ are $1$ and $p$. An integer $n$ is a composite number if $(\exists a,b)(n=ab \wedge |a| < |n| \wedge |b| < |n|)$.

3.0b DO   Every integer other than $0$ and $\pm 1$ is either a prime number, or the negative of a prime number, or a composite number.

3.1 HW (4 points) Determine, for which integers $m$ is the following statement true:   "$m$ is not a divisor of any prime number." Your answer should be a clear and simple statement. No proof required.

3.2 HW Find all sets $A\subseteq\zzz$ for which the following statement is true:

• $(\forall x\in\zzz)((x\in A) \Rightarrow (x$ is a prime number and $x\equiv 6 \pmod{21}))$

3.5 STUDY the slides of today's lecture ($\tt slides21.pdf$); they cover today's material in detail.

3.6 REVIEW the definitions of injective and surjective maps (functions) in the slides. Note: "function" and "map" are synonyms.

3.7 NOTATION: For integers $n\ge 0$ we write $[n]$ to denote the set   $[n]=\{1,2,\dots,n\}\,.$
Examples: $[4]=\{1,2,3,4\}$,   $[1]=\{1\}$,  $[0]=\emptyset$

3.8 DO   $|[n]|=n$.

3.10 NOTATION   Recall that $B^A$ denotes the set of functions with domain $A$ and codomain $B$, i.e., the functions $f:A\to B$.

3.12 HW (4 points) Describe all functions with empty codomain. Your description should be simple and explicit. Note that to describe a function, first you have to state the domain and the codomain. -- How may such functions are there?

3.20 DEF   Let $f\in B^A$ and $g\in A^B$ be functions.
(a) We say that $g$ is a left inverse of $f$ if $(\forall x\in A)(g(f(x))=x)$.
(b) We say that $g$ is a right inverse of $f$ if $(\forall y\in B)(f(g(y))=y)$.
(c) We say that $g$ is the inverse of $f$ if $g$ is both a right inverse and a left inverse of $f$. We also refer to the inverse as the 2-sided inverse for emphsis. We say that $f$ is invertible if it has an inverse.

3.22 DO   Prove: $f\in B^A$ cannot have more than one inverse. The unique inverse (if exists) is denoted $f^{-1}$.

3.24   Prove: HW (a) (5 points) $f\in B^A$ has a left inverse if and only if $f$ is injective.
DO: (b) $f$ has a right inverse if and only if $f$ is surjective.
DO: (c) $f$ is invertible if and only if $f$ is bijective.

3.26 HW (5 points)   Prove: If $f\in B^A$ has a right inverse, $r$, and a left inverse, $\ell$, then $r=\ell$. The proof should be just one or two lines. (Note: two functions $r,\ell:A^B$ are equal by definition if $(\forall b\in B)(r(b)=\ell(b))$.)

3.28 DO   Prove: If $f\in B^A$ has a left inverse and a right inverse then $f$ is invertible. (Use the preceding exercise.)

3.30 DO   Let $f\in B^A$. Recall:
(a) If $f$ is injective then $|A|\le |B|$.
(b) If $f$ is surjective then $|A|\ge |B|$.
(c) If $f$ is bijective then $|A|=|B|$.

3.31 DO   Let $f\in B^A$ where $|A|=|B|=n$. Prove:
$f$ is injective $\iff$ $f$ is surjective $\iff$ $f$ is bijective.

3.32 DO   Prove: If $A,B\subseteq \zzz$ are finite sets then $|A+B|\le |A|\cdot |B|$. Give a proof by finding a surjection $f: A\times B\to A+B$ and then using 3.30(b). (Review this proof in the slides.)

3.34 HW (5 points)   Find $k,n\ge 1$ and a function $f\in [n]^{[k]}$ such that $f$ has a unique left inverse (i.e., it has exactly one left inverse) but no right inverse.

3.35 Bonus (5 points)   Let $k\ge 2, n\ge 0$ and let $f\in [n]^{[k]}$. Prove: If $f$ has a left inverse but no right inverse then the left inverse is not unique.

3.40 DO   Count the $[n]\to [n]$ bijections.
The answer is $n!$ ($n$-factorial); prove.

3.42 DO   Count the $[k]\to [n]$ injections.
The answer is $n(n-1)\cdots(n-k+1)$. Prove.

3.44 Bonus (5 points)   Let $n\ge 0$. Count the surjections $f:[n+1]\to [n]$. Your answer should be a closed-form expression (no summation or product signs) using the factorial function.

3.46 HW (4 points)   Count the $[n]\to [2]$ surjections. Your answer should be a closed-form expression.

3.50 HW (5 points)   Let $O_n$ denote the set of odd subsets of $[n]$ (subsets of odd size), and $E_n$ the set of even subsets. For all $n\ge 1$, construct a bijection $f_n:O_n \to E_n$. Prove that your function is bijective by stating its inverse. The definition of $f_n$ should be very simple.

3.55 FACT (Pigeonhole principle, PHP)   If $|A| > |B|$ and $f\in B^A$ then $f$ is not injective.

3.57 DO   Prove that the PHP is equivalent to the statement that   "If $f\in B^A$ is injective then $|A|\le |B|$."

3.60 Bonus (8 points)   Let $n\ge 1$ and let $S\subseteq [2n]$ be a subset of size $|S|\ge n+1$. Prove: $(\exists a,b\in S)(a\neq b$ and $a\mid b$)$.

3.61 (4 points) HW   Prove that the in the previous exercise, the lower bound $|S|\ge n+1$ is tight for every $n\ge 1$, i.e., the conclusion fails if we permit $S$ to have $n$ elements.
So what you need to do is the following. For every $n\ge 1$, find a subset $T_n\subseteq [2n]$ such that $|T_n|=n$ and $(\forall a,b\in T_n)(a\mid b \Rightarrow a=b)$.

3.70 DO   Prove:   $(\forall x\in\rrr)(1+x\le \eee^x)$.

3.72 REVIEW the Birthday paradox from the slides, including the application of 3.70 in the proof.

3.80 DEF   Let $A,B,C\subseteq\zzz$. We say that $C$ is the direct sum of $A$ and $B$ if every element of $C$ can uniquely be written as the sum of an element of $A$ and an element of $B$. In other words, $C\subseteq\zzz$ is the direct sum of $A,B\subseteq\zzz$ if the following holds:   $(\forall c\in C)(\exists! a\in A, b\in B)(c=a+b)$.   We denote the circumstance by $C=A\oplus B$.   (LaTeX:   A \oplus B.)

3.81 DO   If $C=A\oplus B$ then $C=A+B$ but not conversely.

3.83 DO   Let $A,B$ be finite subsets of $\zzz$. Prove: $A+B=A\oplus B$ if and only if $|A+B|=|A|\cdot |B|$.

3.85 Bonus (5 points)   Let $\nnn_0$ denote the set of non-negative integers. Find $A, B\subseteq \nnn_0$ such that $|A|=100$ and $\nnn_0=A\oplus B$.

3.88 CH   Find two infinite sets $A, B\subseteq \nnn_0$ such that $\nnn_0 = A\oplus B$.

Class 2, Thu 10-1   Sets
All HW problems will be due Monday, October 5, 11:59pm, except where otherwise stated. Late homework will not be accepted. Do NOT turn in the "DO" exercises, but do solve them; otherwise you risk being left behind. Use the LaTeX HW template provided (click on the banner).

2.10 DEF Subset We say that the set $A$ is a subset of the set $B$ if $(\forall x)(x\in A \implies x\in B)$. We denote this circumstance by $A\subseteq B$.   For example, $\{a,b,a,a\}\subseteq \{a,c,b\}$.

2.12 When are two sets equal? Let $A,B$ be sets. Then $A=B \iff (\forall x)(x\in A \iff x\in B)$. In other words, $A$ and $B$ have the same elements.   For example, $\{a, c, a, b, c\} = \{a ,c ,b\} = \{a, b, c\}$. There is just one empty set $\emptyset$ defined by $(\forall x)(x\notin \emptyset)$.

2.14 DO   Prove: $A=B$ if and only if $A\subseteq B$ and $B\subseteq A$.

2.16 DEF (sumset)   Let $A,B$ be subsets of $\zzz$, the set of integers. We define their sumset as   $A+B = \{a+b \mid a\in A, b\in B\}$.   This is an example of the "setmaker bar" notation; the bar reads "such that."

2.18 Example   Let $A=\{3,4,5,8\}$ and $B=\{1,6,7\}$. Then $A+B = \{4,5,6,9,10,11,12,14,15\}$.

2.20 DO   Prove:  $A+B=\{c\in\zzz\mid (\exists x\in A)(\exists y\in B)(c=x+y)\}$

2.22 DO   $A+\emptyset = \emptyset$.

2.24 NOTATION   For a set $A$ we write $|A|$ to denote the number of elements of $A$, also called the cardinality of $A$, or simply the size of $A$. For instance, $|\{a,c,a,b,c\}|=3.$

2.26 Bonus (6 points) (due Monday, October 12) Let $A,B$ be non-empty finite subsets of $\zzz$. Prove:   $|A+B|\ge |A|+|B|-1.$

2.28 DO   Prove that the upper bound given in the preceding exercise is tight. In other words, for all $k,\ell\ge 1$, find $A,B\subseteq\zzz$ such that $|A|=k$, $|B|=\ell$, and $|A+B|=k+\ell-1$.

2.30 DO   Let $A,B$ be finite subsets of $\zzz$. Prove:   $|A+B|\le |A|\cdot |B|$.

2.32 DEF   Let $A\subseteq \zzz$ and $k\in \zzz$. Then $kA = \{ka \mid a\in A\}$.

2.34 Examples (DO: verify!):   $1\zzz=\zzz$,   $2\zzz=\{\text{even numbers}\}$,   $0\zzz =\{0\}$.

2.36 DO   $(\forall a\in\zzz)(a\mid a)$. NOTE: this is true even for $a=0$ (why?):   $0\mid 0$.

2.38 DO   $b\in kA \iff (\exists a\in A)(b=ka)\}$.

2.40 DO   $k\zzz = \{b\in\zzz\mid k\text{ divides }b\}$.

2.42 HW (4 points) Find $k\in\zzz$ such that $4\zzz + 6\zzz = k\zzz$. No proof required.

2.44 DEF (intersection) $A\cap B= \{x\mid x\in A\text{ and }x\in B\}$.

2.46 HW (4 points) Find $\ell\in\zzz$ such that $4\zzz \cap 6\zzz = \ell\zzz$. No proof required.

2.50 CONVENTION   If we state a formula with free variables such as $(pq)r=p(qr)$, the intended meaning is that the formula holds for all choices of those free variables, as if they were universally quantified: $(\forall p,q,r)((pq)r=p(qr))$.

2.52 DEF We say that the sets $A$ and $B$ are disjoint if $A\cap B=\emptyset$. We say that the sets $A_1,\dots,A_k$ are disjoint if they are pairwise disjoint, i.e., if for every $i\neq j$ in the range $1\le i,j\le k$, the sets $A_i$ and $A_j$ are disjoint.

2.54 DO (Union bound) Let $A_1,\dots, A_k$ be sets. (a) Prove:
$$\left|\bigcup_{i=1}^k A_i\right| \le \sum_{i=1}^k |A_i|\,.$$ (b) Prove: equality holds in this inequality (i.e., the two sides are equal) if and only if the $A_i$ are disjoint.

2.56 DEF   Let $A$ be a set. The powerset $\calP(A)$ is the set of all subsets of $A$.

2.58 DO   Prove: If $|A|=n$ then $|\calP(A)|=2^n$.

2.60 DEF   The Cartesian product of the sets $A$ and $B$ is the set $A\times B=\{(a,b)\mid a\in A, b\in B\}$.

2.62 DO   Prove: If $A,B$ are finite sets then $|A\times B|=|A|\cdot |B|$.

2.64 DEF   A relation $R$ between two sets, $A$ and $B$, is a subset $R\subseteq A\times B$.

2.66 DO   Prove: If $|A|=k$ and $|B|=\ell$ then the number of relations between $A$ and $B$ is $2^{k\ell}$.

2.68 DEF   A function with domain $A$ and codomain $B$ is defined by a relation $R\subseteq A\times B$ such that $(\forall a\in A)(\exists! b\in B)((a,b)\in R)$. Here $(\exists! b)$ means there exists a unique $b$. So if $(a,b_1)\in R$ and $(a,b_2)\in R$ then $b_1=b_2$. We denote this unique $b$ by $f(a)$ and we refer to $f$ as a function $f:A\to B$. So the relation corresponding to this function consists of the pairs $(a,f(a))$ $(a\in A)$. The set $R_f :=\{(a,f(a))\mid a\in A\}$ is called the graph of the function $f$.

2.70 DO   Let $f:A\to B$ be a function and let $R_f$ be the graph of $f$. Show that $|R_f|=|A|$.

2.72 DO   Count the functions $f:A\to B$. Show that the number of such functions is $|B|^{|A|}$.

2.74 NOTATION. The set of functions $f:A\to B$ is denoted $B^A$. So the preceding exercise says that $\left|B^A\right|=|B|^{|A|}$.

2.76 DEF   Let $f\in B^A$ be a function. Let $a_1, a_2\in A$, $a_1\neq a_2$. We say that $a_1$ and $a_2$ collide if $f(a_1)=f(a_2)$. In this case, we call the unordered pair $\{a_1,a_2\}$ a collision. Let us write $\coll(f)$ for the number of collisions of $f$.

2.78 DO   (a) Let $f\in B^A$ be a function. Let $|A|=n$. Prove:   $\coll(f)\le n(n-1)/2$.   Find all functions $f\in B^A$ such that $\coll(f)=n(n-1)/2$. Prove that $\coll(f)=n(n-1)/2$ if and only if $f$ is a constant function, i.e., $(\exists b\in B)(\forall a\in A)(f(a)=b)$.

2.80 DEF   We call the function $f:A\to B$ an injection or an injective function if $\coll(f)=0$.

2.82 DO   Prove: the function $f\in B^A$ is injective if and only if $(\forall x,y\in A)(f(x)=f(y) \implies x=y)$.

2.84 DO   Let $|A|=k$ and $|B|=n$. Count the $A\to B$ injections. Show that the number of $A\to B$ injections is $n(n-1)\cdots(n-k+1)$. This number can also be written as $n!/(n-k)!$, but this expression is not useful when $k$ is relatively small compared to $n$.

2.86 FACT (Pigeonhole principle)   If $|A| > |B|$ and $f\in B^A$ then $f$ is not injective.

Class 1, Tue 9-29   Quantifiers, divisibility, congruence
All HW problems will be due Monday, October 5, 11:59pm, except where otherwise stated. Late homework will not be accepted. Do NOT turn in the "DO" exercises, but do solve them; otherwise you risk being left behind. Use the LaTeX HW template provided (click on the banner).

In all problems in this problems sets, all variables are integers.

1.10 Our most important sets of numbers:

•    $\nnn=\{1,2,3,\dots\}$    natural numbers
•    $\zzz=\{\dots, -3, -2, -1, 0, 1,2,3,\dots\}$    integers
•    $\qqq$    rational numbers
•    $\rrr$    real numbers
•    $\ccc$    complex numbers

1.12 Each of these domain has two arithmetic operations: addition and multiplication. Identities that hold in each of these domains:

• $a+b=b+a$   commutativity of addition
• $ab=ba$   commutativity of multiplication
• $(a+b)+c=a+(b+c)$   associativity of addition
• $(ab)c=a(bc)$   associativity of multiplication
• $a(b+c)=ab+ac$   distributivity

1.14 In the domains $\zzz$, $\qqq$, $\rrr$ we have an ordering relation "$\le$". One of the properties of this relation is transitivity:
If $a\le b$ and $b\le c$ then $a\le c$.

1.20 "Number Theory": focus on $\zzz$
Central concept: divisibility
Examples: "$8$ divides $48$" and "$8$ does not divide $28$"
Notation  $8\mid 48$,  $8\nmid 28$
Terminology.  All of the following statements are synonymous:

•   $8$ divides $48$
•   $8$ is a divisor of $48$
•   $48$ is a multiple of $8$
•   $48$ is divisible by $8$

1.22 DEF (divisibility) Let $a,b\in\zzz$. We say that $a$ divides $b$ if $(\exists x\in\zzz)(ax=b)$ ("there exists $x$ such that $ax=b$").

We refer to such an $x$ as a witness of the relation $a\mid b$. Example: $x=6$ is a witness of the relation $8\mid 48$.

1.24 DO: Question: is $0\mid 0$?   Answer: YES!   Witness: $x=83$ (or any other value; in this case, there are infinitely many witnesses).

1.26 Quantifiers:   organizers of mathematical statements

• $\exists$:   existential quantifier   "there exists $\dots$ such that"
• $\forall$:   universal quantifier   "for all"

1.30 Identities are universal statements: all variables are univerally quantified. Example:

distributivity:   $(\forall a,b,c)(a(b+c)=ac+bc)$

1.32 CONVENTION. We often omit the universal quantifiers from such a statement and just write $a(b+c)=ac+bc$ but if we do so, the universal quantifiers should be clear from the context. (For instance, we have to say that we talking about identities as opposed to equations.)

1.34 Caution: the validity of statements depends on the universe.

Example:   $(\forall a\neq 0)(\exists x)(ax=1)$

1.34 DO This statement is TRUE over $\rrr$ and FALSE over $\zzz$. ("Over $\rrr$" means "if the universe is $\rrr$.")

1.36 CONVENTION. For the remaining problems in this sequence, our universe will be $\zzz$.

1.38 Fact: (Transitivity of divisibility) $(\forall a,b,c)(((a\mid b)\wedge(b\mid c))\implies (a\mid c))$
($\wedge$ means "AND", $\vee$ means "OR".)

1.40 DO: Prove this fact. From what property of basic arithmetic (rules of additin and multipication) does this fact follow?
Answer.   From the associativity of multiplication.

1.42 Method of proof.
Let us translate the assumptions to basic arithmetic:   $(\exists x)(ax=b)$ and $(\exists y)(by=c)$.
The desired conclusion is $(\exists z)(az=c)$.
Guess the witness $z$ using witnesses $x,y$: let $z=xy$.
Check that it works: $c=by=(ax)y=a(xy)=az$. We used the associativity of multiplication. So
associativity of multiplication $\implies$ transitivity of divisibility.

1.44 DO: prove the following result.
Proposition (a little theorem): If $d\mid a$ and $d\mid b$ then $d\mid a\pm b$. (This is a shorthand for "$(d\mid a+b) \wedge (d\mid a-b)$".)
This is a universal statement; I omitted the universal quantifier. So what the statement means is $(\forall a,b,d)(((d\mid a)\wedge(d\mid b))\implies (d\mid a\pm b))$.
State, what property of basic arithmetic did you use in the proof.
Answer to the last part of the question: from distributivity.

1.46 DO Prove: If $a\mid b$ then $\pm a\mid \pm b$. (Again, I omitted the universal quantifier, and I will follow this practice below. The two $\pm$ signs combine to four statements, one of which is $-a\mid b$, for example.)

1.48 DO (a) Find all divisors of the number $0$.
  (b) Find all divisors of the number $1$.
  (c) What is the number of divisors of a prime number?

1.50 DO True or false? If true, prove; if false, give a counterexample.
(a) $x\mid y \implies x\le y$    (b) $(x\mid y)\wedge(y\ge 0)\implies x\le y$    (c) $(x\mid y)\wedge(y > 0)\implies x\le y$.

1.52 HW (4 points) Find a value $m$ such that the following statement is true:   $(\forall x)((4 \mid x) \wedge (6 \mid x)\iff (m\mid x))$. No proof required.

1.54 DO Prove: $x-y \mid x^2-y^2$.

1.56 DO Prove: $(\forall k\ge 0)(x-y\mid x^k-y^k)$.

1.58 HW (6 points) Find all values of $x$ such that $x+1\mid x^2+1$. Prove that you found all of them.

1.60 HW (5+4 points) (a) Find a pair $(x,y)$ of integers such that $5\le x < y$ and $x\mid y$ and $x+1\mid y+1$.   Briefly tell, how you found your solution.
(b) Find infinitely many pairs $(x,y)$ with this property.

1.62 Bonus (6 points) Find $5\le x < y$ such that $x+i\mid y+i$ holds for $i=0,1,\dots,100$.   (Added Oct 4, 11pm: you only need to find one such pair $(x,y)$.) (Explanation updated Oct 5, 2pm: you need to find a pair $(x,y)$ such that $5\le x < y$ and $x\mid y$ and $x+1\mid y+1$ and $x+2\mid y+2$ and $\dots$ and $x+100 \mid y+100$ all hold simultaneously.)

1.70 DIVISOR GAME. Fix an integer $n\ge 2$. Two players alternate picking positive divisors of $n$. Divisors of a number picked cannot be picked in the future. The player forced to pick $n$ loses.
EXAMPLE: $n=30$. First move: Player 1 picks 10. This rules out picking 10, 5, 2, or 1 in the future.
Second move: Player 2 picks 3. (So in the future neither player can pick 10, 5, 3, 2, or 1.) Third move: Player 1 picks 6. Fourth move: Player 2 picks 15. Now all maximal divisors of 30 (6,10,15) have been picked, so Player 1 is left with no choice but to pick 30 in the Fifth move, and loses.

1.72 DO   Prove that if $n=30$ and Player 1 begins with any number other than 1 then Player 1 loses (assuming Player 2 plays right).

1.74 DO   Prove: for $n=30$, Player 1 has a winning strategy. What is the first move of Player 1 ?

1.76 DO   Prove: for $n=81$, Player 1 has an easy winning strategy. (More generally, Player 1 easily wins if $n$ is a prime power ($n=p^k$ for some prime $p$ and $k\ge 1$)). What is the first move of Player 1 ?

1.78 DO   Prove: for $n=36$, Player 1 has an easy winning strategy. (More generally, Player 1 easily wins if $n$ is of the form $n=p^2q^2$ where $p,q$ are distinct primes.) What is the first move of Player 1? What is their strategy?

1.80 CH   For every $n\ge 2$, Player 1 has a winning strategy.

1.90 DEF   We say that $a$ is congruent to $b$ modulo $m$ if $m\mid a-b$. We denote this circumstance by $a\equiv b\pmod m$.

1.92 Examples.   $5\equiv 23 \pmod 9$,  $4\equiv -21 \pmod 5$,   $3\equiv 1\pmod 2$.

1.94 HW (2+2+2 points) Express in simple and common English, without referring to the concept of divisibility, when two numbers are congruent (a) modulo 2, (b) modulo 1, (c) modulo 0.

1.96 DO   Prove that every number is congruent to (a) 0 or 1 modulo 2   (b) 0 or $\pm1$ modulo 3   (c) 0, $\pm1$, $\pm2$, or 3 modulo 6.

1.98 HW (4 points) Prove: If $p$ is a prime number and $p\ge 5$ then $p\equiv \pm 1\pmod 6$.

1.100 HW (6 points) Find all values of $x$ such that $x^2\equiv 4 \pmod x$. Prove that you found all such values.

1.102 DO   Prove that congruence modulo $m$ is a transitive relation:
If $a\equiv b\pmod m$ and $b\equiv c\pmod m$ then $a\equiv c\pmod m$.
First translate the assumptions and the desired conclusion to the language of divisibility; then refer to a result about divisibility. Which result?

1.104 DO   Prove that congruence modulo $m$ is additive:
If $a\equiv x \pmod m$ and $b\equiv y \pmod m$ then $a+b\equiv x+y \pmod m$.
First translate the assumptions and the desired conclusion to the language of divisibility; then refer to a result about divisibility. Which result?

1.106 DO   (Lemma to the multiplicativity of congruence) Prove: If $a\equiv b \pmod m$ then $(\forall c)(ac\equiv bc \pmod m)$.
First translate the assumption and the desired conclusion to the language of divisibility; then refer to a result about divisibility. Which result?

1.108 HW (4 points)   Prove that congruence modulo $m$ is multiplicative:
If $a\equiv x \pmod m$ and $b\equiv y \pmod m$ then $ab\equiv xy \pmod m$.
Do NOT translate the assumptions and the desired conclusion to the language of divisibility. Instead, give a quick solution by combining two of the DO exercises above. You can use those exercises without proof.

1.110 DO   Prove: If $a\equiv b\pmod m$ then $(\forall k\ge 0)(a^k\equiv b^k\pmod m)$.
Use induction on $k$ and use the multiplicativity of congruence.

1.112 HW (4 points)   Find a value $m$ such that the following statement is true:   $(\forall x,y)(((x\equiv y\pmod 4) \wedge (x\equiv y\pmod 6))\iff (x\equiv y \pmod m)))$. No proof required.

1.114 HW (4 points)  Prove: If $x$ is odd then $x^2\equiv 1\pmod 8$.

1.116 Bonus (6 points) (due Monday, October 12)  Let $d(n)$ denote the number of positive divisors of the number $n$. For instance, $d(4)=3$ and $d(6)=4$. Determine, for exactly which positive integeres $n$ is the number $d(n)$ odd. Prove your answer.   Hint. Experiment with $n\le 30$, find a pattern, make a conjecture, prove.